高温高压深井完井射孔段套管断裂力学分析
仝少凯,徐晓航,冯 琦,巨全利,吕占国,康 楠
(西安石油大学a.机械工程学院;b.石油工程学院,西安710065) ①
在高温高压深井套管射孔完井作业过程中,井下套管处在极为复杂恶劣的环境中,特别是封隔器以下套管受射孔冲击力的影响,受力状态瞬间发生改变,出现瞬间失稳、脉动、甚至弯曲折断现象,给后续投产作业带来很大的困难。射孔完井作业结束后,井下套管要为油气产出提供可靠、安全的井筒准备,而此时带有“射孔孔眼”的套管能否满足后续投产作业的要求是一项迫切需要解决的难题。
油田现场应用和相关统计资料显示:油层套管发生损坏失效的位置大都在射孔部位,且射孔套管受力和变形比较复杂;由于射孔引起的应力集中更容易造成套管变形损坏,其中一个重要原因是长期以来对射孔作业后套管强度降低没有足够的认识,虽然经过射孔后套管强度有所减弱,但未掌握明确的数量概念。相关试验结果认为,是由射孔孔眼孔边应力腐蚀开裂所导致的。
目前,国内外对油层射孔套管进行的理论与试验方面的研究不多,文献[1]分析了套管损坏形态及射孔对套管损坏的影响,并提出了预防措施;文献[2]利用ANSYS有限元软件建立了油层射孔段套管仿真模型,对射孔段进行局部挤压变形模拟,分析了射孔段套管的应力;文献[3]采用有限元法建立了射孔段套管力学模型,分析了射孔段套管的剩余壁厚,确定了不同壁厚的套管承受不同载荷状态下的承载能力;文献[4]针对港西油田出砂层位,研究了出砂引起套管损坏力学条件,建立了油层部位射孔段套管屈曲力学模型,指出射孔后套管强度降低,射孔部位易发生弯曲;文献[5]分析了载荷对套管作用机理,指出由于射孔、地层压力等因素造成射孔段套管强度减小,导致套管柱整体可靠度降低,发生失效的可能性加大。
为了有效地解决这一难题,本文提出应用断裂力学理论进行高温高压深井完井射孔段套管的应力和强度安全性分析,以期优选合理的射孔施工、储层改造等工艺参数,对确保油层射孔套管不受损坏、提高其使用寿命具有十分重要的经济意义和理论价值。
1 模型的建立
将射孔段套管看作带有“圆孔”形贯穿裂纹(射孔孔眼)的无限大圆柱筒壳体,如图1所示。分析带环向裂纹圆柱筒形壳体在内压pi和外压po共同作用下,裂纹尖端附近的应力场和圆柱筒壳体的整体强度。由于射孔孔眼属于空间对称贯穿裂纹,因此沿套管轴线方向展开,如图2所示。
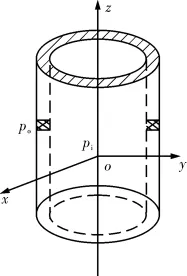
图1 受内、外压的射孔段套管

图2 受内、外压的射孔段套管展开示意
2 基本方程的建立
为便于分析,作如下基本假设:
1) 射孔套管是均匀、连续、各向同性的圆柱壳体。
2) 当产生很小变形时,射孔套管满足虎克定律。
2.1 平衡微分方程
现从射孔套管圆柱筒壳体的中面上取一微面dx·dy,微面上受内压pi(x,y)和外压po(x,y)的作用,如图3所示。微面上所受的内力如图4~5所示。

图3 射孔段套管微面示意

图4 射孔段套管微面上所受外力和内力示意
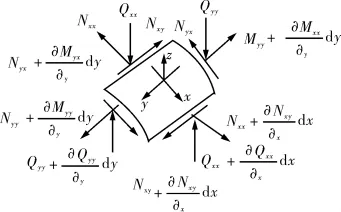
图5 射孔段套管微面上所受内力偶矩示意
根据平面力学原理,微面上的力和力偶矩必须满足6个平衡条件,即3个力平衡和3个力偶矩平衡。由于没有体力的作用,再略去y方向的剪力Qyy对环向的影响,则由图4~5可得中面内的平衡条件为

即


化简整理得

略去高阶微量有

式中:Nxx、Nyy为射孔套管在x、y方向上的法向力,kN;Nxy、Nyx为射孔套管在xy 平面上的顺剪力,kN。
根据微分方程理论和格林函数,求式(2)~(3)的通解为

式中:Φ(x,y)为射孔套管的应力函数。
再由中面外的平衡条件∑Fz=0,∑My=0,∑Mx=0可得

化简整理得

式中:Qxx、Qyy为射孔套管在x、y方向上的剪力,kN;pi为射孔套管的内压,MPa;po为射孔套管的外压,MPa;槇Rc为射孔套管的平均半径,mm。
在2个力矩平衡方程中略去Mxy、Myx、Qxx、Qyy的高阶微量,考虑Mxy=Myx,则有

联立式(8)~(9)得

将式(10)代入式(7),整理得

式中:Mxx、Myy为射孔套管在x、y方向上的力矩,N·m;Mxy为射孔套管在xy平面上的力矩,N·m。
2.2 几何方程
考虑射孔套管中面上任一点位移和应变的关系,设u、v、w为中面上任一点沿坐标轴x、y、z方向的位移分量,εxo、εyo、γxyo为中面上任一点沿各坐标轴的应变分量。
根据弹性力学理论[6],中面内任一点的环向应变εyo为
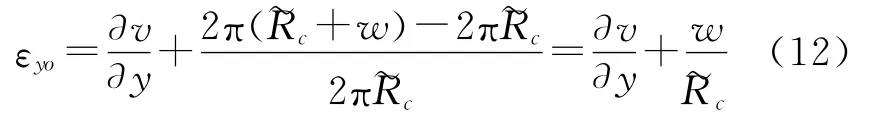
故中面上任一点应变与位移间的关系为

消去u和v,可得中面应变与法向位移间的连续方程为

因此,射孔段套管平行曲面上任一点的应变与位移间的关系为

式中:εxx为射孔套管平行曲面上任一点的轴向应变;εyy为射孔套管平行曲面上任一点的环向应变;γxy为射孔套管平行曲面上任一点的切应变。
2.3 物理方程
根据材料力学知识[7],在平面应力状态下,由广义虎克定律可知

由于套管上的射孔孔眼属于贯穿裂纹,则将式(16)在套管筒壳体壁厚t方向上进行积分,结合式(15)得内力与变形的关系为

式中:E为射孔套管材料的弹性模量,MPa;μ为射孔套管材料的泊松比;t为射孔套管的壁厚,mm;D
将式(17)变为
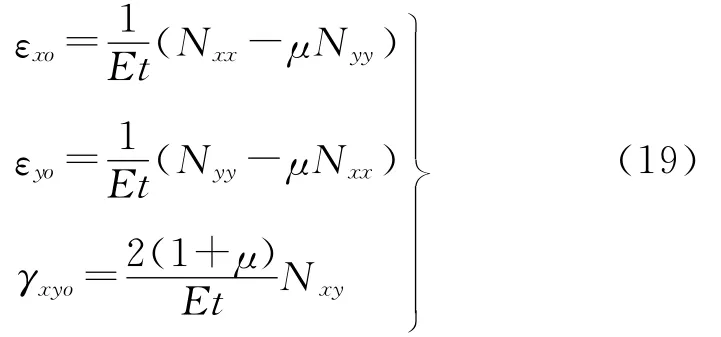
2.4 方程综合
采用混合法对以上各方程加以综合。
将式(19)、式(5)代入式(14),化简得
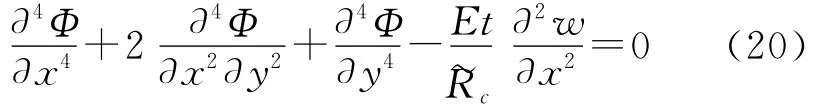
将式(18)代入式(11),整理得

式(22)第1式为相容方程,第2式为平衡方程。此式即为由混合法所推导出的圆柱筒壳体的基本微分方程组。只要确定应力函数Φ和位移函数w,利用边界条件即可求解。
由于射孔段套管射孔孔眼属于环向贯穿裂纹,如图6所示。采用无量纲坐标α、β。

图6 带环向裂纹(射孔孔眼)受内、外压的射孔段套管
故由式(22)改写得到带环向裂纹射孔段套管在内、外压联合作用下的基本微分方程为

3 基本方程的求解
根据断裂力学理论[8-9],结合文献[10-12],采用数值法求解射孔段套管的基本微分方程。引入一个复变函数Γ,即

将式 (23)变为

此方程的解为

其中的Γ1和Γ2满足如下方程,即

设式(27)的解为

式中:e为自然超越数,且e=2.718 28。
将式(28)代入式(27)可知Ψ1、Ψ2满足同一个方程,即

然后,借助贝塞尔函数乘积形式的马丢函数[13],在椭圆坐标系(ρ,θ)下,利用边界条件:

得到射孔段套管射孔孔眼裂纹附近的应力函数Φ和法向位移函数w的表达式为

射孔段套管射孔孔眼裂纹附近法向位移函数的复合参数C的计算式为

式(34)表征了与射孔套管材料、载荷、孔眼尺寸等相关的常数,为式(33)的待定参数。
弯曲应力场为

式中:pbc为带有环向贯穿裂纹的射孔段套管受内、外压时,在裂纹附近处的奇异性弯曲应力场参数,MPa。其表达式为

式中:pec为带有环向裂纹的射孔段套管受内、外压时,在裂纹附近处的奇异性拉伸应力场参数,MPa。其表达式为


原始套管应力问题属厚壁圆筒问题[6-7],利用Lame公式得到在内压pi和外压po共同作用下原始套管的轴向拉应力为

在套管外压较小时,即po=0时,轴向拉应力为

式中:Rci为原始套管的内半径,mm;Rco为原始套管的外半径,mm。
4 套管强度分析
4.1 塑性屈服判据和强度条件
根据弹塑性力学理论中的米赛斯(Mises)判据[14],即当复杂应力状态下的形状改变比能等于单向拉伸屈服时的形状改变比能时,材料就出现屈服。Mises塑性屈服判据为

式中:σxd4为射孔套管第四相当应力,MPa;σs为射孔套管材料的屈服极限,MPa。

据此可导出射孔段套管的弯曲屈服判据和拉伸屈服判据。
若不考虑外压po,即po=0时,根据 Mises塑性屈服判据可得到初始弯曲屈服和初始拉伸屈服时射孔段套管的内压pbsi和pesi,故综合安全范围要求取射孔段套管的临界屈服内压psi为

式(45)可保证在此内压psi范围内射孔段套管不发生塑性屈服,但还不能保证是否满足强度要求,因此需要满足强度条件。
按照第四强度理论得到的强度条件为[7]

式中:[σ]为射孔套管材料的许用应力,MPa。
由式(46)可求得满足强度要求的射孔段套管的最大内压pmsi。故为确保射孔段套管不发生塑性屈服,同时满足后续投产作业强度要求的最佳临界内压{}为

利用断裂力学理论分析射孔段套管的强度安全性,目的是要保证带缺陷的套管既不要使其开裂,又要保证不会发生失稳破坏而有一定的安全裕度。此时,式(46)中的许用应力[σ]按照下式计算,即

式中:σf为射孔套管的断裂应力,MPa;nf为射孔套管的安全裕度,按照压力容器设计方法,取nf=2.7。
在最佳临界内压{p*si}条件下,将式(48)代入式(46)可求得射孔段套管射孔孔眼的许用尺寸[rk],要求射孔孔眼的实际尺寸rk小于许用尺寸,则保证安全。因此,确保射孔段套管安全的充要条件是射孔段套管所承受的合成应力和实际射孔孔眼尺寸在容许范围以内,即

4.2 断裂判据
射孔段套管的断裂分析是建立在应力强度因子判据的基础上的。根据断裂力学理论,带环向贯穿裂纹的射孔段套管受内、外压共同作用时,射孔孔眼附近的拉伸应力场和弯曲应力场的应力强度因子

因此,按照射孔段套管材料应力强度因子提出的断裂判据为

式中:KIC为射孔段套管断裂的临界应力强度因子,由相关手册获取。
5 结论
1) 将射孔段套管看作带有“圆孔”形贯穿裂纹(射孔孔眼)的无限大圆柱筒壳体模型是合理的,是应用断裂力学分析的首要条件。
2) 射孔段套管内表面处射孔孔眼附近的应力最大,外表面处射孔孔眼附近的应力最小。
3) 射孔段套管射孔孔眼的尺寸和孔眼边缘的完整性(即粗糙度)极大地影响射孔孔眼附近的应力分布:射孔孔眼直径减小,裂纹逐渐逼近I型裂纹,应力场强度增强;射孔孔眼直径增大,应力场强度降低;孔眼边缘越粗糙,应力开裂越明显,相应地应力场强度也越强。建议优选射孔器和射孔施工工艺参数。
4) 射孔段套管在内、外压联合作用下射孔孔眼附近的应力场分布规律为:外压一定时,内压增大,应力场增强;内压一定时,外压增大,应力场减弱;当不考虑外压时,射孔孔眼附近的应力场强弱变化与内压大小变化一致。建议应合理地控制压裂、酸化等储层改造工艺参数。
5) 油层套管射孔后强度显著降低,造成射孔段套管实际承载能力远低于设计能力。建议在油层套管设计时考虑射孔造成套管强度降低这一因素,以确保油层套管射孔后有足够的强度富裕。
[1] 唐 明,金有海,刘 猛.套管损坏形态分析及预防措施[J].石油矿场机械,2007,36(9):7-10.
[2] 彭 凯,贾星兰,张全胜.不同注水压力下射孔套管的ANSYS分析[J].石油矿场机械,2008,37(1):46-48.
[3] 王苏玲,叶鑫锐,秦庆忠.注水井反冲洗套管承载能力有限元分析[J].石油矿场机械,2009,38(1):31-34.
[4] 任丽华,王凤祥,刘建东,等.大港港西油田出砂对套损的影响分析[J].石油矿场机械,2010,39(6):28-31.
[5] 王光磊,李文飞,周延军.高酸性气田套管柱安全可靠性评价方法研究[J].石油矿场机械,2011,40(9):1-5.
[6] 徐芝纶.弹性力学(上册)[M].北京:高等教育出版社,2006.
[7] 刘鸿文.材料力学(II)[M].北京:高等教育出版社,2004.
[8] 北京钢铁研究院金属物理室.工程断裂力学:上册[M].北京:国防工业出版社,1977.
[9] 范天佑.断裂力学基础[M].南京:江苏科技出版社,1978.
[10] 孙训方.带裂纹的压力容器的断裂力学分析[J].实验力学,1980,26(3):1-10.
[11] 林绍东.带环向裂纹受内压圆柱壳裂纹尖端附近的应力分析[J].西南石油学院学报,1982,4(16):26-34.
[12] 潘家华.断裂力学在油气管道工程上的应用[C]//管道科学技术科学报告会论文集,1980:293-230.
[13] 王竹溪,郭敦仁.特殊函数概论[M].北京:科学出版社,1979.
[14] 李同林.弹塑性力学[M].武汉:中国地质大学出版社,2006.
——以准噶尔盆地玛湖凹陷致密砾岩为例

