弹性势能零点选择与弹性势能表达式问题讨论
张红明
(北京师范大学附中 北京 100052)
新课标人教版高中《物理·必修2》第七章第5节“探究弹性势能的表达式”说一说栏目,“在以上探究中我们规定,弹簧处于自然状态下,也就是既不伸长也不缩短时的势能为零势能.能不能规定弹簧某一长度时的势能为零势能?说说你的想法.”[1~3]
仔细分析,上述观点出现了一个不正确的表达式
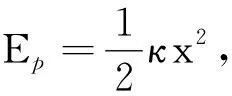
1 弹性势能零点的不同选择对弹性势能表达式的影响
1.1 弹性势能的引入
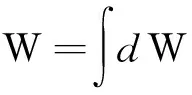
(1)
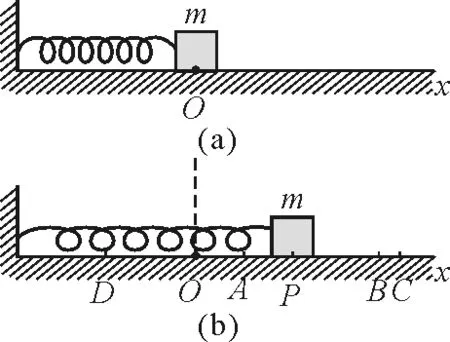
图1
可见,弹性力做功仅由弹簧的劲度系数κ和系统的初始位置和终了位置决定,而与系统经过的路径无关,这表明,弹性力是保守力,从而可引入相关的势能——弹性势能.
在高中教材中,弹性势能的引入是从现象中切入的,“发生弹性形变的物体能够对外做功,因而,具有能量,把这种能量叫做弹性势能.”这种方式没有把势能的特点揭示出来,可以说是教材的一种缺陷,这样,必然导致学生在学习弹性势能时先天不足.
1.2 弹性势能及势能差
保守力及其相关势能的定义为保守力所做的功等于物体与该保守力相关势能的减少量.
在图1(b)中,若设物块m在A与B时的弹性势能分别为EpA和EpB,则由以上定义及式(1)应有
ΔEAB=EpA-EpB=WAB=
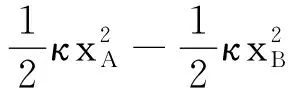
(2)
式中ΔEAB是物块m在A和B两位置时的弹性势能差,这是一个确定的值,不会因为弹性势能的零点选择而改变.但当规定弹性势能的零点位置不同时,系统的弹性势能却有不同的表达式.
1.3 弹性势能零点的不同选择对其表达式的影响
(1)当选择弹簧的自由长度(不伸长亦不缩短)处系统的弹性势能值为零时,由图1(b)中A和B两点为任意,便可以将A点选在原点O处,即有xA=0,这时EpA=EpO=0,于是由式(2)得
即
因为B点是任意的,可以去掉下标而有
(3)
该式即为选择弹簧自由长度处为弹性势能零点时,所具有的弹性势能的一般表达式.
(2)当选择弹性势能零点在弹簧有一伸长量xA的A点(A点确定后,x即为一常量,我们用x0表示之,即xA=x0)时,有EpA=0,这时由式(2)得
由于B点是任意的,仍可去掉下标写成
(4)
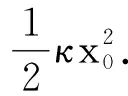
的形式,而只能是式(4)所表示的形式.
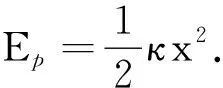
2 从弹簧振子的振动能量看零势能点的选择
高中物理教材在讲述振幅的物理意义时,指出振幅是表示振动强弱的物理量.在讲述简谐振动的能量时,这样写道,“弹簧振子和单摆在振动过程中动能和势能不断地发生变化.在平衡位置,动能最大,势能最小;在位移最大时,势能最大,动能为零.在任意时刻动能和势能的总和,就是振动系统的总机械能.振动系统的机械能跟振幅有关,振幅越大,机械能就越大.”
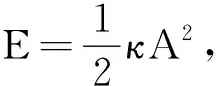
弹簧振子做简谐振动的动力学方程为
其中
该方程的解为简谐运动的运动学方程,可写作
x=Acos(ωt+α)
关于振子的动能,应用质点的动能公式
得
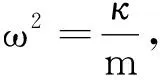
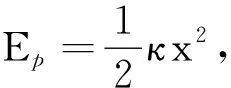
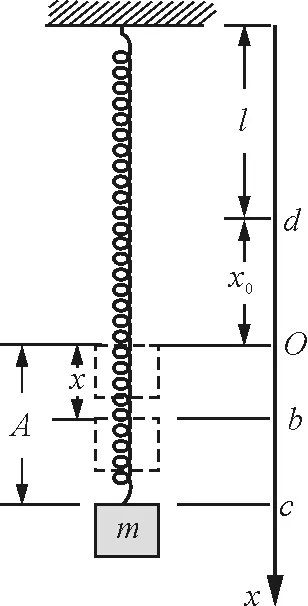
图2
如图2,弹簧振子系统的弹簧质量可忽略,其原长为l.当挂上一物体m并静止时,端点在O点处(这时弹簧有一伸长量x0,且κx0=mg).取O点为原点,向下为x轴正向建立坐标.当系统振动时,振幅为A(即最大位移为A),该时刻物体在c点,系统的弹性势能表示式为:
(1)取弹簧自然长度为弹性势能零点(即Epd=0),物体在各位置时,系统的弹性势能各为
这一系统的重力势能同样选取d点处为重力势能零点时,各位置的重力势能分别为
为与弹性势能区别,这里E都带撇.
当将弹性势能、重力势能的零点都选在弹簧原长位置时,各点的总势能为
考虑到平衡时,有mg=κx0,代入以上各式得
从上式可知,当选择了弹簧原长位置d为弹性势能和重力势能的零点后,竖直悬挂的弹簧振子在各点总势能的表达式从形式上看不能写成
(2)若选取平衡位置O点处为弹性势能零点(EpO=0),则物体在各位置时,弹性势能的值可由计算弹性力的功而得
显然两种情况下,弹性势能表达式是不一样的.
这一系统的重力势能在选取O点处为重力势能零点时,各位置的重力势能分别为
当将弹性势能、重力势能的零点都选在平衡位置时,各点的总势能为
考虑到平衡时,有mg=κx0,代入以上各式得
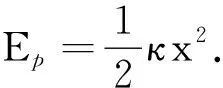
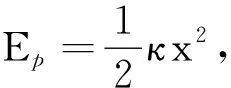
据上述分析,似乎得出弹簧振子对零势能点的选取有特殊的要求,其实不然.
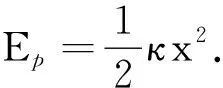
取弹簧自然长度为弹性势能零点(即Epd=0),物体在各位置时,系统的弹性势能各为

解得
将κx0=mg代入得
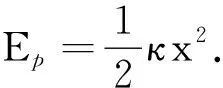
以竖直弹簧振子为例,将最低点的系统总势能和平衡位置处系统总势能相比较,增加的弹性势能为
增加的重力势能为
总的势能增加为
此即振动的总能量.
3 物理学中关于势能的一般性定义
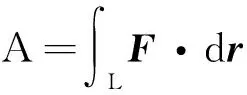
参考文献
1 人民教育出版社课程教材研究所.普通高中课程标准实验教科书.北京:人民教育出版社,2006
2 人民教育出版社物理室.全日制普通高级中学教科书.北京:人民教育出版社,2003
3 赵凯华,张维善.新概念高中物理读本(第二册).北京:人民教育出版社,2006
4 漆安慎,杜婵英.普通物理教程·力学.北京:高等教育出版社,2001
5 张宪魁.物理科学方法教育.北京:科学出版社,2002

