旋转矢量法的对称性分析*

尹社会 曹辉

(河南工业职业技术学院 河南 南阳 473009)

旋转矢量法是直观研究简谐振动的几何方法，在分析简谐振动的合成驻波[1～3]、受迫振动[4]以及“拍”现象[5]等问题的研究中非常有效.对称性分析则是贯穿于整个物理学的几乎所有分支，比如,在力学、电磁学、光学、热学中的应用等，它在基本粒子物理学中更是必不可少的重要手段之一，甚至在物理实验中对称性思维也处处闪烁着睿智的火花，像圆环摆实验中仪器的设置、物理天平测质量的交换法、桥式电路的平衡分析法等.

本文拟结合振动和波中的问题用旋转矢量法处理过程做对称性分析.

1 旋转矢量法的本质

简谐振动的运动学方程为

x=Acos(ωt+φ0)

(1)

式(1)中x表示质点偏离平衡位置的位移，A表示简谐振动的振幅，ω表示简谐振动的固有角频率，φ0表示初相位，ωt+φ0表示相位.

下面考虑旋转矢量.如图1所示，设在t=0时，矢量A与x轴的夹角为φ0，使矢量A以匀角速度ω绕点O逆时针旋转，则在任意时刻t，矢量A与x轴的夹角为ωt+φ0，则矢量A末端点M在x轴上投影点的运动方程为

x=Acos(ωt+φ0)

这与简谐振动的运动学方程具有相同的形式，所以,可以用矢量表示简谐振动，这种方法就称为旋转矢量法.比较波动方程和振动方程会发现，振动方程初相位变为随着位移而变化的形式就是描述波的传播形式的波动方程，因此，波动方程也可以采用旋转矢量法来描述.旋转矢量法就是指在旋转矢量与正弦量之间存在着一一对应关系的情况下，用旋转矢量表示正弦量的一种几何方法.

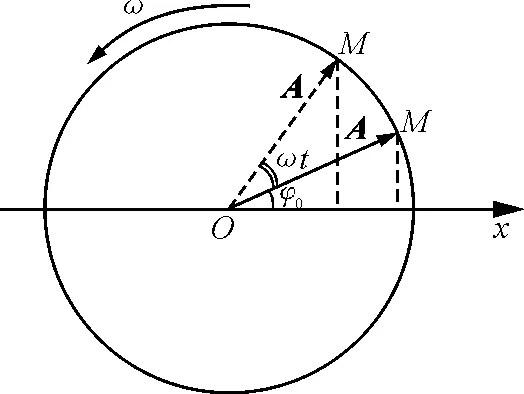
图1 旋转矢量示意图

这里矢量旋转所围绕的点是坐标原点O，表示简谐振动的平衡位置，旋转矢量的长度等于简谐振动的振幅，旋转矢量与轴的夹角表示简谐振动的相位.

2 驻波的旋转矢量法合成

一般的驻波是由入射波和界面处反射回来的反射波叠加形成的.假设初始时刻，入射波某一波峰位置为坐标原点，一般即为振源所在位置，界面距原点的距离为l，角频率为ω，入射波振幅为A，反射波振幅为A′，则入射波和反射波方程分别为

y=Acos(ωt-kx)

(2)

y′=A′cos(ωt+kx-2kl-β)

(3)

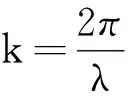
当A′=A时，由式(2)和式(3)可得到合成波为驻波，其方程为

(4)

若A′≠A，其合成波的表达式就不易用分析法来处理了.至于合成波是否为驻波及其与振幅和二者的初相位之间的关系如何就更难以定论.因此，采用旋转矢量法是处理这类问题的首选方案.

下面简单讨论几种情形.

(1)当A′=A，l=λ，β=0时，式(3)可简化为

y′=Acos(ωt+kx)

(5)

图2 两列波合成矢量图

在t=0时，由矢量图(图2)可以直接看出合成波的振幅为2Acoskx，初相位为α=0，驻波方程为

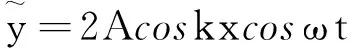
(6)

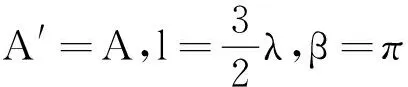
y′=Acos(ωt+kx-π)

(7)

图3 两列波合成矢量图

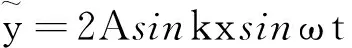
(8)

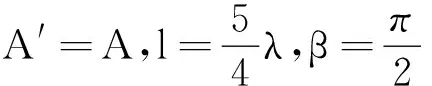
(9)

(10)

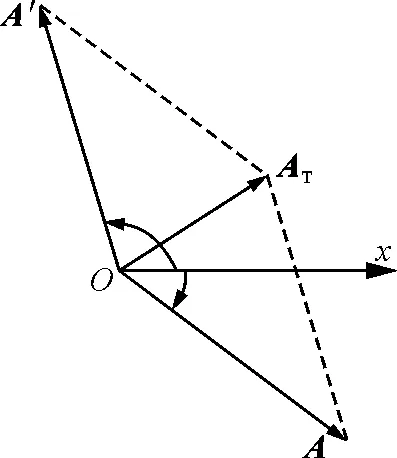
图4 两列波合成矢量图

由上述3种情形可以看出，t>0时方程的形式不发生变化，表现在旋转矢量图中A沿顺时针方向转动，A′沿逆时针方向转动，由对称性可知，合矢量AT方向不变.

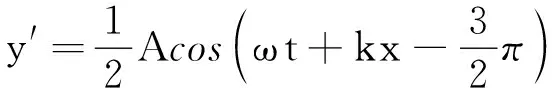
(11)

图5 两列波合成矢量图

在t=0时，由矢量图(图5)可以直接看出合成波的振幅为

初相位为

驻波方程为

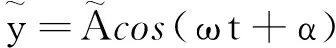
(12)

在上述情形中，t>0时，在旋转矢量图中，A沿顺时针方向转动，A′沿逆时针方向转动，由于对称性遭到破坏，可知合矢量AT方向不再保持不变，对应的量的计算也就变得比较复杂，我们一般不再进行具体的计算，但是定性的分析还是很方便的.通过分析这些特例，可以看出，当反射波振幅不等于入射波振幅时，合成波就不再是驻波，而是一种复杂的波动情形.

3 旋转矢量法分析受迫振动

系统在周期性外力作用下被迫进行的振动称为受迫振动.假设系统中为轻质弹簧，忽略弹簧质量，其劲度系数为κ，振子的质量为m，周期性外力为F0cosωt，阻尼力与速度成反比，记作f=-cv，c为阻尼系数.则受迫振动的动力学方程为

(13)

通常的做法是求解这个非齐次常系数微分方程，数学计算比较复杂.如果采用旋转矢量法分析会直观简单得多.本文中的旋转矢量是广义上的，既包括位移旋转矢量，也包括速度旋转矢量和加速度旋转矢量.在讨论受迫振动等问题时，就是这个意义上的旋转矢量.

假设受迫振动达到稳定状态时的运动学方程为x=Acos(ωt-δ)，则式(13)中各项分别用旋转矢量表示可记为

F=B+C+D

(14)

通过简单的计算分析表明B⊥C,C⊥D.

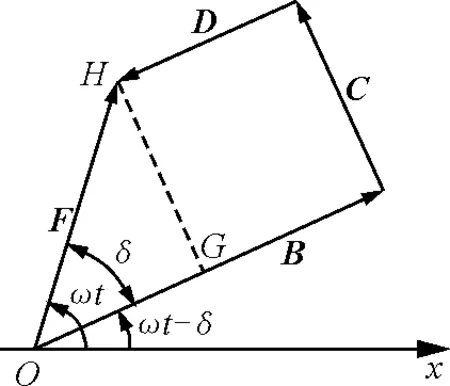
图6 受迫振动旋转矢量图

如图6所示，图中B,C,D,F分别表示对应的旋转矢量，根据图示容易求出受迫振动的振幅和初相位.

4 旋转矢量法分析“拍”现象

在谈到同方向不同频率的简谐振动的合成时，一般都会涉及到“拍”现象.所谓“拍”现象是指两个频率都比较大，而两频率之差却不大的同方向简谐振动合成时，合振动的振幅就会出现时大时小的现象.由于稳频激光器的出现，光拍频现象很容易实现.光拍频技术已经是无线电技术中非常重要的技术之一.如果把光的拍频和光的干涉现象进行对比研究会发现，它们都是强度随相位差而发生变化的一种运动形式.对于光的干涉只是由于空间观测点的不同，两束光的光程差不同，造成了强度随空间变化的分布.光的拍频是因为两束光有频差，随时间的变化而引起相位的变化而表现出的强度随时间变化的形式.如果我们采取旋转矢量法分析光的“拍”现象，从理论上是可行的，并已经有人进行了相关研究[5].这样,就能够把旋转矢量法的简洁、直观的特性显露出来，这里不再赘述，详情请参考文献[5].

5 旋转矢量法的对称性分析

若规定用顺时针旋转的矢量表示沿轴负方向传播的行波，用逆时针旋转的矢量表示沿轴正方向传播的行波，两者叠加，得到一个不再旋转，模随时间呈周期性变化的矢量表示驻波[6].这一结论非常直观，有助于学生把握驻波现象的本质.

在处理驻波的问题中，从矢量图上看，当合成图形为菱形时，即振幅相等时，该系统具有几何对称性，合成的波为驻波.当合成图形不是菱形时，系统失去了几何对称性，其合成波也不再是驻波.

在研究受迫振动时，应用的正是自然数为底的指数函数的导数形式不变的特性，根据欧拉公式，反映到旋转矢量图中就是位移旋转矢量与速度旋转矢量相互垂直，速度旋转矢量与加速度旋转矢量相互垂直这一特性.

在光“拍”现象的问题中，虽然表面上看旋转矢量法只是在表述方式上直观形象，其实也正是其本质上的对称性导致这一方法的有效性.

参考文献

1 李增林.用旋转矢量法研究驻波问题.大学物理,1993(2):24～26

2 张韬，李奇楠.用旋转矢量分析驻波.齐齐哈尔大学学报，2001(4)：69～72

3 苏景顺.用旋转矢量分析驻波.河北建筑工程学院学报，2011(4)：94～97

4 徐友文，许弟余.用旋转矢量法求受迫振动的振幅和初相.物理与工程,2006(4)：20～21

5 苏未安，陈秀洪.用旋转矢量法研究“拍”现象.江西理工大学学报，2009(1)：60～63

6 杨庆怡，刘奕新，郭进.用旋转矢量描述波形及振动曲线与波形的转换.广西科学院学报，2010(2)：107～109