水从高处下落时碎裂现象的力学原理分析*

黄婷

(广西民族师范学院物理与电子工程系 广西 崇左 532200)

生活蕴藏着物理，物理离不开生活，利用物理知识来分析、解释生活中各种奇妙的现象是体现“从生活走向物理”理念的主要途径，同时体现出物理本身的无穷魅力.在日常生活中，常常会看到这样的现象，从高台向下倒水，大片的水在下落的过程中突然分散开来，水滴破碎时的样子如同天女散花，十分好看.而不同大小的水滴碎裂的时间点和碎裂时下落的距离也不同，为什么会出现这样的现象呢？下面从力学的角度来进行分析.

1 水滴下落时为什么会碎裂

水滴下落时，在空气动力的作用下以多种形式裂化，裂化形式取决于水滴周围的气体流动模式，椭球形形变是在较稳定气流中产生也最常见的一种.水滴在下落过程中受气体压力作用将水滴由球形逐渐压扁为椭球形、杯形及半水泡形.当水滴与气流的相对速度大于临界速度时，半水泡形水滴的上部首先爆裂，形成边缘厚度不均的环状，气流吹在环状液滴上使边缘撕裂成片状，中心形成大量的小水泡，最终碎裂成各种尺寸的细小水滴或小水泡[1].

2 水滴运动方程的确定

在水滴下落过程中，无风情况下，将质量为m，密度为ρ的水滴简化为一半径为r的球形，为了计算方便，作如下假设：

(1)水滴在下落过程中其温度、粘性、密度等介质参数不变.

(2)由于水滴密度远大于空气密度，由压力梯度而引起的力和表观质量力都很小.可忽略不计，同时还可忽略气动升力，因此只考虑作用在水滴上的空气阻力和重力.

在理论力学中所说的“与物体速度一次方成正比的阻力”，指的就是粘滞阻力.在空气中运动速度不十分快的物体，受到的阻力主要是粘滞阻力.水滴下落的速度比较小且假设跟空气没有相对速度，所以近似地认为空气阻力F与水滴速度的一次方成正比[2]，即

F阻=-kv=-6πηrv

(1)

式中，η为粘滞系数；v为水滴下落的速度；r为水滴的半径.

由牛顿第二定律，水滴运动方程可写成

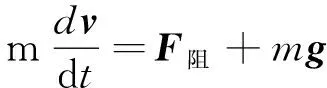
(2)

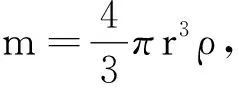
(3)

由于水滴沿竖直方向运动，并取水滴运动方向为正.整理式(3)可得

(4)

设t=0时，v=0，对式(4)进行一次积分得

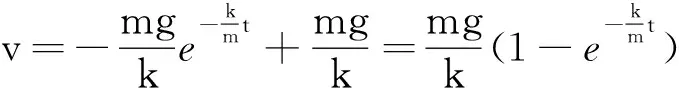
(5)

对式(5)再积分一次，并利用初始条件t=0时，y=0定积分常数，可得水滴下落的距离与时间的关系为

(6)

3 水滴破碎条件

由文献[1]可知，水滴碎裂主要与阻力和表面张力之比的韦伯数We有关，而

(7)

式中，ρg为空气密度，σ为水的表面张力系数，D为水滴的直径，ud为气液体的流速差，因为本文中令空气静止，所以ud就为水滴的下落速度v，则韦伯数变为

(8)

水滴碎裂的条件为[1]

(9)

整理得水滴碎裂时的临界韦伯数为

(10)

式中，CD是取决于碎裂条件的常数，带有下标“b”的参数为碎裂时的参数.由式(10)可得到水滴在某一速度v下，最大的稳定直径

(11)

文献[3]研究指出当液体相对速度较低时，8≤We≤30.所以取一个韦伯数We，带入式(10)，就可得到碎裂条件的常数CD，如果已知水滴的直径，根据式(11)就可以算出水滴碎裂的速度.由前面推导出的式(5)和式(6)，又可以求出碎裂的时间和碎裂的位置.

(1)水滴碎裂时的临界速度

(12)

(2)水滴碎裂时的时间

由式(5)得

(13)

(3)水滴碎裂时已下落的距离

把碎裂的时间带入式(6)，可以求出水滴碎裂时已下落的距离为

(14)

4 结论

在稳定的气流中，水滴下落过程中的碎裂除了跟无量纲的韦伯数We有关外，还与水滴的直径D,水的表面张力σ,空气密度ρg以及水的粘滞系数η有关，而水的表面张力σ,空气密度ρg以及水的粘滞系数η一般是定值，如果韦伯数We取定，水滴的直径越大，就越快碎裂，下落的距离就越小.

参考文献

1 曹建明.喷雾学.北京:机械工业出版社,2005.20～21

2 漆安慎,杜婵英.力学基础.北京:高等教育出版社,1982. 60

3 蔡斌,李磊,王照林. 液滴在气流中破碎的数值分析.工程热物理学报，2003，24(4)：613～616