错在哪里——兼谈圆周运动中的一类最值问题

徐秀娟 王兴堂

（江苏省沛县中学 江苏 徐州 221600）

【题目】图1为“S”字形玩具轨道.该轨道是用内壁光滑的薄壁细圆管弯成，固定在竖直平面内.轨道弯曲部分是由两个半径相等的半圆连接而成，圆半径比细管内径大得多，轨道底端与水平地面相切.弹射装置将一个小球（可视为质点）从a点水平弹射向b点并进入轨道，经过轨道后从P点水平抛出，已知小球与地面ab段间的动摩擦因数μ＝0.2，不计其他机械能损失，ab段长L＝1.25m，圆的半径R＝0.1m，小球质量m＝0.1kg，轨道质量为M＝0.15 kg，g＝10m／s2.

图1

求：（1）若va＝5m／s，小球从P点抛出后的水平射程；

（2）若va＝5m／s，小球经过轨道的最高点时，管道对小球作用力的大小和方向；

（3）设小球进入轨道之前，轨道对地面的压力大小等于轨道自身的重力，当va至少为多少时，轨道对地面的压力为零.

解析：原题答案（1）、（2）略.

（3）分析可知，要使小球以最小速度va运动，则当轨道对地面的压力为零，小球的位置应在该“S”形轨道的中间位置，即下面半圆轨道的最高点，设小球在此最高点速度为v，管道对其作用力大小为F′，有

代入数据得

本题所给答案，看起来没有问题，但仔细推敲，却显不够严密，因为，此题所给答案是用圆轨道最高点来分析的，其实小球在到达最高点前对轨道也有压力，有没有可能在轨道的其他位置对轨道压力的竖直分量比在轨道最高点时压力还大，或者说，小球对轨道压力的竖直分量的最大值并不一定在最高点呢？下面我们结合图2做一下简要分析.

图2

如图2所示，圆的半径为R，小球的质量为m，设小球在轨道的最低点速度为v0，且能够到达圆周的最高点.当小球运动到图示位置时，设速度为v，此时轨道对小球的压力为F.由动能定理可得

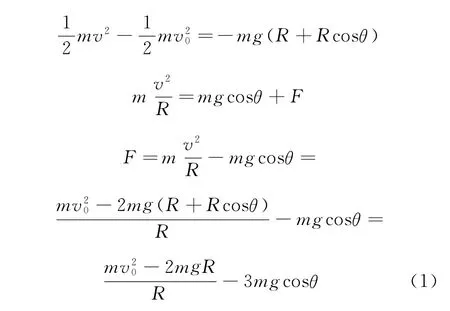
设轨道受到小球压力的竖直分量为F竖

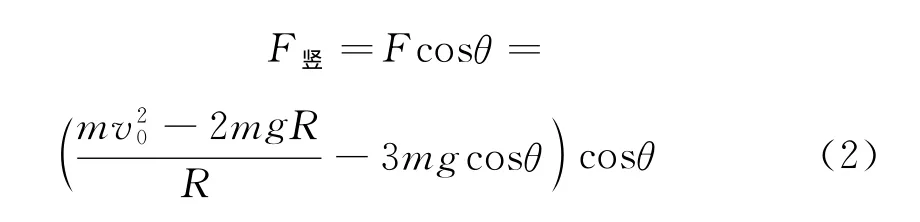
两边同乘3mg，有

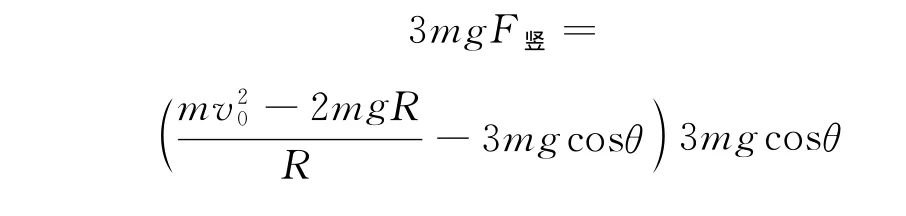
等式右边两项和为定值，由数学知识可知，当

F竖有最大值.

由此可知，在圆周最低点小球的初速度v0不同，最大F竖对应的θ并不同，当v0＜2时，cosθ＜1，表明最大F竖发生在非最高点，此时

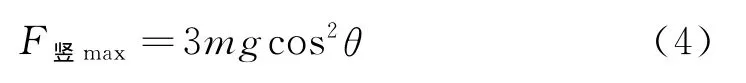
当初速度v0≥2时，利用式（3）求出cosθ≥1，表明F竖max对应的位置应在最高点，此时F竖max≥3mg，且最高点压力随着初速度的增大而增大.

鉴于以上分析，小球对轨道竖直向上压力最大的位置并不一定在最高点.再看本题的第（3）问，要求F竖max＝Mg，而题给条件中Mg＜3mg，也就是说F竖max＜3mg，对比式（4），可知，最大F竖对应的位置并不在最高点，所以原题给出用最高点分析所求的答案应是错误的.

正确解法：由以上分析可知

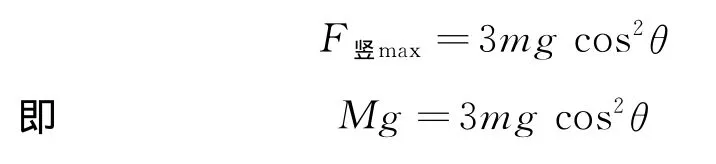
代入数据，可得

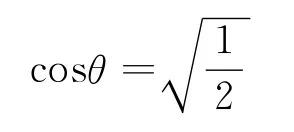
代入式（3），可求得在圆周的最低点时

再对小球在水平面的运动，列动能定理方程有

显然，正确答案要比原题所给答案略小，这是因为本题中小球在最高点的F竖并不是最大，但仍用最高点分析此题，所以求得的初速度值将会偏大.

由于此类问题综合考查了圆周运动、动能定理、物体平衡等知识，此类习题经常出现.但从以上分析可以看出，只有当M≥3mg时，最高点时F竖才最大，当M＜3mg时，F竖最大的位置并不在圆周的最高点，且分析过程比较复杂，因此，建议命题者在命制此类习题要充分认识到此类问题的复杂性，尽量满足M≥3mg，从而降低解题难度.