铁路连续梁拱组合桥箱梁横向受力分析＊

于向东，陈顺平

(1．中南大学土木工程学院，湖南 长沙410075;2．中铁第四勘察设计院集团有限公司，湖北武汉430063)

大跨连续梁拱组合桥作为一种新兴的铁路桥型，将大跨连续梁和拱两种结构体系有机结合在一起，具有结构刚度大、动力稳定性好、跨越能力大、造型美观、施工方便等显著优点［1～3］。连续梁拱组合体系一般采用“先梁后拱”的施工方法［4］，先期恒载主要由梁承担，后期恒载及活载由梁和拱共同承担，各自承担荷载的大小与梁、拱刚度及吊杆的布置有关。因此连续梁拱组合结构箱形主梁的纵、横向受力与普通连续梁均有很大不同。对于箱形截面梁的横向计算，我国的铁路规范明确指出箱梁横截面可按被支承在主梁腹板中心线下缘的箱形框架计算［5］，但它没有说明具体的计算方法和数学模型。一般直接在箱形框架上加刚性支承来求解横向内力［6～8］。这种方法相对简单，在以前设计单线铁路桥梁时曾被广泛采用，并能给出满意的内力分析结果。近年来，随着桥梁向多线发展，结构宽跨比越来越大，这种方法是否适用还需要进一步探讨。尤其对于连续梁拱组合结构，由于吊杆及吊杆处横梁的存在，使箱梁的横向计算更趋复杂化。为了确保结构安全，对于连续梁拱组合结构箱梁横向计算，设计人员一般采用刚性支承和弹性支承进行包络计算［9］，这样没有探明连续梁拱组合结构箱梁横向计算机理，使设计趋于保守。

1 工程概况

本文以温福铁路昆阳特大桥为计算背景［10］，研究连续梁拱组合体系箱梁横向受力特性。昆阳特大桥位于温福铁路与同三高速公路交汇处，跨越同三高速公路及一公路桥，为满足桥下净空要求，同时为尽量降低铁路路肩高程，主桥采用(64+136+64)m预应力混凝土连续箱梁与钢管混凝土拱组合结构，桥型布置如图1所示。主梁采用单箱双室变高度箱形截面，跨中及边支点处梁高3．5 m，中支点处梁高采用7．0 m，梁高按圆曲线变化。箱梁顶宽14．0 m，中支点附近局部顶宽16．1 m，箱梁底宽10．4 m，中支点附近局部底宽12．6 m，具体截面构造见图2。拱肋采用钢管混凝土结构，等高度哑铃形截面，截面高度2．8 m。拱肋弦管直径800 mm，由16 mm厚的钢板卷制而成，弦管之间用δ=16 mm厚钢缀板连接，拱肋弦管及缀板内填充微膨胀混凝土，两榀拱肋间横向中心距11．1 m。吊杆采用PES7－109型平行钢丝束，顺桥向间距8 m，全桥共设14对吊杆。主桥采用“先梁后拱”施工方法。

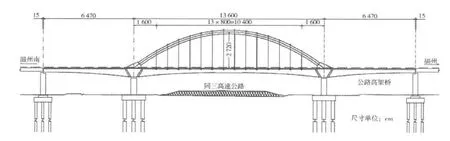
图1 桥型布置图Fig．1 Arrangement of form of bridge

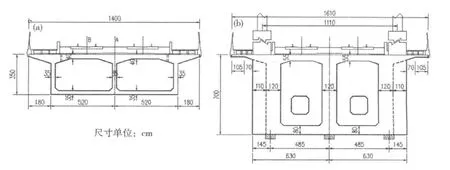
图2 主梁横截面Fig．2 Cross section of main beam

2 箱梁横向应力分析

2．1 计算模型

采用大型通用有限元软件ANSYS建立昆阳桥全桥空间计算模型。主梁采用10个节点的四面体实体单元Solid92模拟，主拱圈和横撑采用Beam4空间梁单元，吊杆采用Link8空间杆单元，吊杆拉力由Link8单元的初应变模拟。全桥共划分为240 974个单元，436 196个节点。约束情况根据支座布置进行模拟，计算坐标原点设左端顶板中心处，顺桥向为X轴，竖向Y轴，横向Z轴，应力拉为正。计算模型见图3。

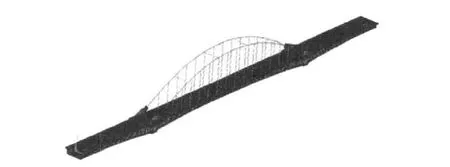
图3 空间有限元模型Fig．3 Spatial finite element model

2．2 箱梁横向应力顺桥向变化趋势

对全桥模型按自重+二恒+ZK活载的最不利荷载工况进行加载，其中ZK活载采用ANSYS参数化设计语言APDL编程进行车道加载。重点对箱梁横向中腹板顶(图2(a)中A截面)及顶板跨中位置(图2(a)中B截面)应力沿顺桥向的变化进行研究，相应位置的应力见图4。

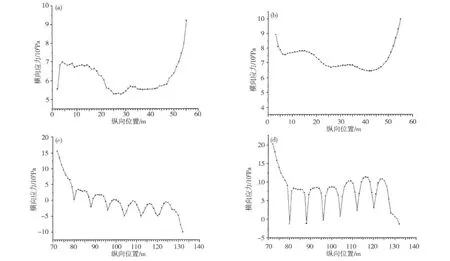
图4 边跨和中跨截面横向应力曲线Fig．4 Transversal stress of sectional flange on side span and middle span

由图4(a)和4(b)可知:边跨中腹板位置顶板上缘横向应力沿纵向的应力曲线起伏较大，在靠近梁端尤其是靠近拱脚处的横向应力比较大，这是因为端横梁和拱脚处横梁承担了较大的横向弯矩，对附近顶板的横向应力有影响;随着离横梁的距离增大，影响逐渐减小。边跨跨度的1/3～2/3跨度段，横向应力变化相对平稳，随着腹板厚度和箱梁高度的综合影响，横向应力逐渐减小，腹板厚度的影响占主导。

由图4(c)和4(d)可知:中跨中腹板位置顶板上缘横向应力顺桥向在靠近拱脚处比较大，随着离拱脚的距离增大，横向应力逐渐减小;经过3个吊杆的距离之后，由于吊杆的拉力作用，抵消了外荷载产生的拉应力，中腹板位置顶板上缘由受拉变为受压，应力图成峰状，峰顶处位置为相邻吊杆区域的中间段，峰谷处为吊杆所在处。并且峰顶和峰谷处的横向应力绝对值随着x的增大而逐渐减小。在中跨跨中段，由于存在截面抗弯刚度较大的中横梁，所以，该处的横向应力绝对值很小。

3 刚性支承框架法与全桥空间计算结果对比

我国的铁路规范明确指出箱梁横截面可按被支承在主梁腹板中心线下缘的箱形框架计算。采用Midas/Civil分别建立边跨无吊杆区域段、中跨吊杆区域段横向框架计算模型，并与Ansys全桥实体模型计算的结果进行对比，以检验刚性支承框架法应用到连续梁拱组合结构横向计算的精度。计算模型节点位置及荷载布置见图5。计算荷载按恒载+单线活载和恒载+双线活载2个工况进行计算，计算结果取最不利值。

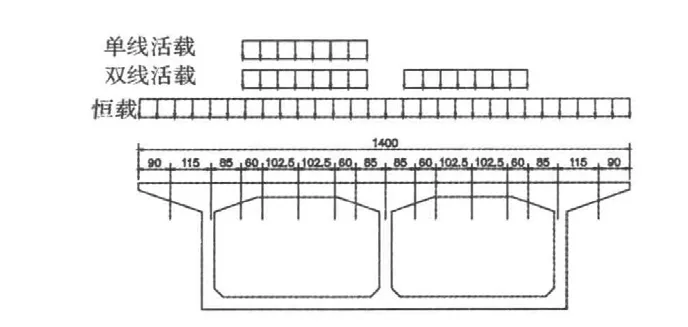
图5 刚性支承框架法节点位置及荷载布置Fig．5 Node Location of rigid － supporting frame method and load distribution

3．1 边跨无吊杆区域段

取单位宽度的截面，在腹板下施加刚性支承，顶板上施加与全桥实体模型对应的荷载，边跨段顺桥向取x为15，30和45 m位置处的截面进行计算，该截面对应的腹板厚度分别为0．35，0．5和0.6 m。计算模型见图6。

图6 边跨刚性支承框架法有限元模型Fig．6 Finite element model of rigid － supporting frame method on side span

x取15，30和45 m位置处采用Midas刚性支承框架法和Ansys全桥实体有限元建模计算的顶板上缘节点横向应力结果如图7所示，横向关键位置应力见表1。

由图7及表1可知:Midas刚性支承框架法计算得到的横向应力曲线图与采用Ansys全桥实体建模计算的横向应力曲线图的规律一致，刚性支承框架法计算结果能够包络全桥实体建模计算结果，验证了刚性支承框架法在无吊杆区域计算横向应力的合理性。

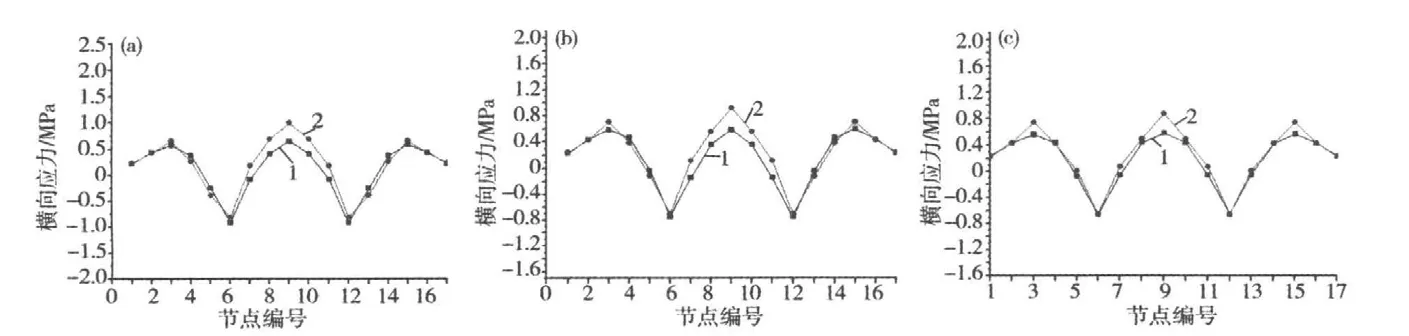
图7 边跨横截面顶板上缘节点横向应力对比Fig．7 Comparison of transverse node－stress of sectional upper flange on side span

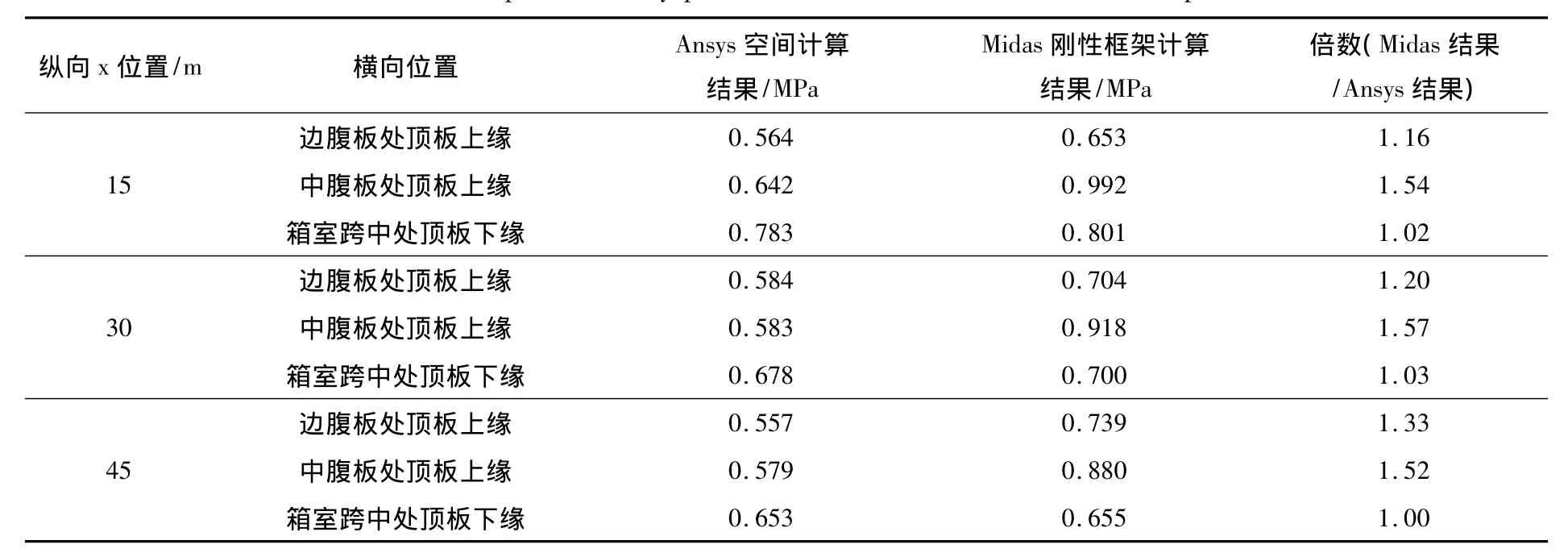
表1 边跨横截面关键位置应力对比Table 1 Comparison of key positional stress of cross section on side span

对于边腹板处顶板上缘处的横向应力极值，刚性支承框架法计算结果为Ansys计算结果的1．2倍左右;对于中腹板处顶板上缘处的横向应力极值，刚性支承框架法计算结果为Ansys计算结果的1．5倍以上;对于箱室跨中处顶板下缘处的横向应力极值，刚性支承框架法计算结果与Ansys计算结果很吻合。在设计中，若采用刚性支承框架法计算无吊杆区域顶板的横向应力，可按此规律对相应位置处的计算结果进行折减。

3．2 中跨有吊杆区域段

取跨中D7吊杆区(x=128 m)截面进行横向应力分析，该截面的腹板厚度分别为0．35 m。因为吊杆力的影响，顺桥向计算宽度就不能再简单的取1m宽进行计算，取1 m和2 m(吊杆间距的1/4)、2．7 m(吊杆间距的 1/3)、4 m(吊杆间距的1/2)的框架宽度进行比较分析。计算模型见图8。应力计算结果见图9。

图8 中跨刚性支承框架法有限元模型Fig．8 Finite element model of rigid － supporting frame method on middle span

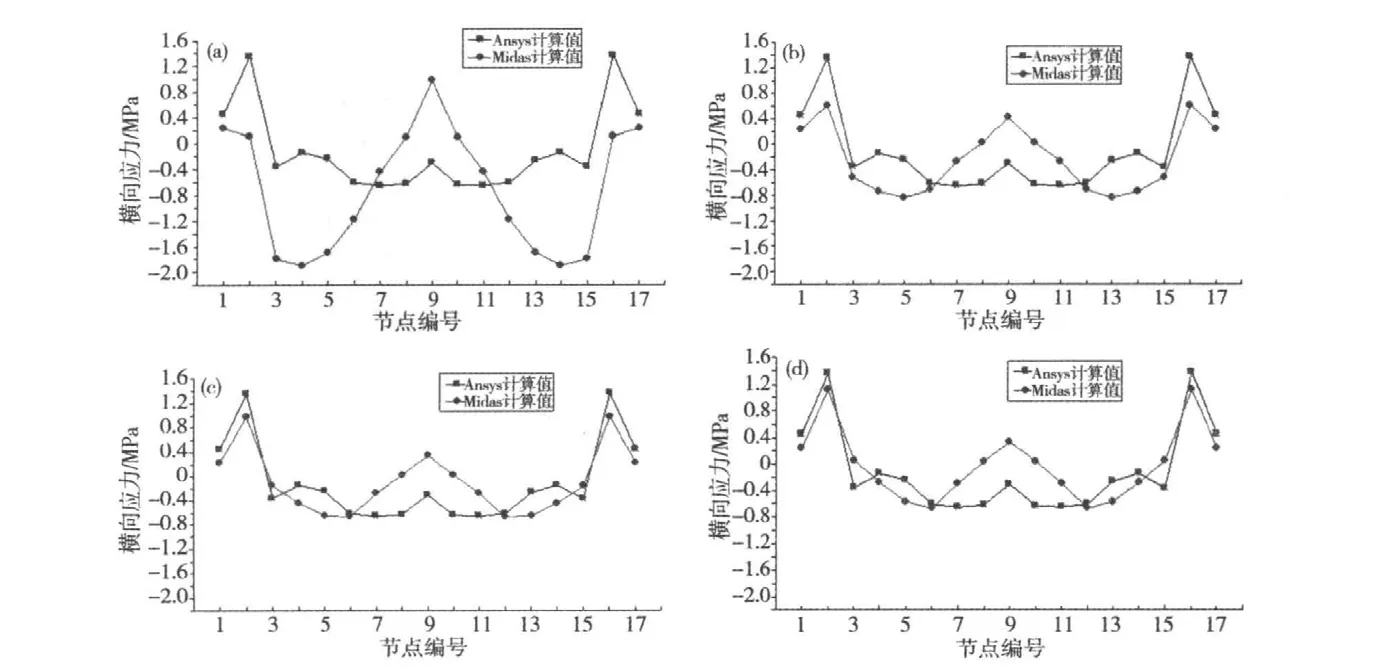
图9 顺桥向不同宽度框架与全桥空间计算结果对比Fig．9 Resultant comparison of different width frame of bridge in axial direction with spatial structure

由以上计算结果可知:吊杆位置处应力集中比较明显，靠近该位置的节点横向应力比较大，此处横向配筋应予加强。由于吊杆力的影响，边腹板和中腹板处顶板上缘应力均为压应力。采用Midas刚性支承框架法计算时如果取单位宽框架则不能反映这一特征，取2．7 m和4．0 m宽框架时则能很好反映这一特征，并且与Ansys全桥空间计算结果基本一致。因此建议:对于有吊杆区域，横向框架宽度取吊杆间距的1/3或以上进行计算。

4 结论

(1)由于吊杆的拉力作用，连续梁拱组合结构箱梁横向应力顺桥向的变化成峰状，并且峰顶和峰谷处的横向应力绝对值随着向跨中靠近而逐渐减小。

(2)对于连续梁拱组合结构边跨无吊杆区域，Midas刚性支承框架法计算得到的横向应力曲线图与采用Ansys全桥实体建模计算的横向应力曲线图的规律一致，刚性支承框架法计算结果能够包络全桥实体建模计算结果，验证了刚性支承框架法在无吊杆区域计算横向应力的合理性。

(3)对于连续梁拱组合结构中跨有吊杆区域，采用刚性支承框架法计算横向应力，横向框架宽度应取吊杆间距的1/3或以上进行计算。

［1］罗世东．铁路桥梁大跨度组合桥式结构的应用研究［J］．铁道标准设计，2005(11):1 －4．LUO Shidong．Research on the application of long － span combined bridge for railway bridge［J］．Railway Standard Design，2005(11):1 －4．

［2］孙树礼．连续梁拱组合桥梁设计关键技术对策研究［J］．铁道标准设计，2005(5):25 －28．SUN Shuli．Research on the key technologies＇countermeasures in the design of combined bridges with prestressed continuous beam and arch［J］．Railway Standard Design，2005(5):25－28．

［3］李国平．连续拱梁组合桥的性能与特点［J］．桥梁建设，1999(1):10－13．LI Guoping．Performance and characteristic of continuous composite arch bridge［J］．Bridge Construction，1999(1):10－13．

［4］陈元清，李小波．温福铁路昆阳特大桥施工控制［J］．世界桥梁，2011(3):37－40．CHEN Yuanqing，LI Xiaobo．Construction control of kunyang bridge on Wenzhou—Fuzhou railway［J］．World Bridges，2011(3):37 －40．

［5］TB 10002．3—2005，铁路桥涵钢筋混凝土和预应力混凝土结构设计规范［S］．TB 10002．3—2005，Code for design on reinforced and prestressed concrete structure of railway bridge and culvert［S］．

［6］Babu Kurian and Devdas Menon．Correction of errors in simplified transverse bending analysis of concrete boxgirder bridges［J］．J Bridge Eng，2005．10:650 －657．

［7］吴再新，贺国京，罗世东，等．宜昌长江大桥箱梁横向受力性能研究［J］．中国铁道科学，2005(4):11－15．WU Zaixin，HE Guojing，LUO Shidong，et al．Study on the transverse mechanical characteristics of Yichang Yangtze River Bridge box girder［J］．China Railway Science，2005(4):11－15．

［8］王晖，项贻强．拱梁组合式连续梁桥横向分布研究［J］．公路交通科技，2006(12):99－101．WANG Hui，XIANG Yiqiang．Research on load lateral distribution of continuous girder and arch combination bridge［J］．Journal of Highway and Transportation Research and Development，2006(12):99 －101．

［9］康小英，高丽，文望青．高速铁路大跨度连续梁拱桥设计［J］．铁道建筑技术，2009(z1):89－93．KANG Xiaoying，GAO Li，WEN Wangqing．Design of long－span continuous beam－arch combined bridge for high speed railway bridge［J］．Railway Construction Technology，2009(z1):89 －93．

［10］黄纳新，严爱国，罗世东．温福铁路昆阳特大桥主桥连续梁拱施工设计［J］．铁道标准设计，2005(11):31－33．HUANG Naxin，YAN Aiguo，LUO Shidong．The construction design for the composite structure of the continuous beam arch in the major part of kunyang super long bridge over Wenzhou － Fuzhou Railway［J］．Railway Standard Design，2005(11):31 －33．