多跨连续梁合龙顺序的优化以及混凝土初始加载龄期的探讨＊

方淑君，肖啸，李杰

(中南大学土木工程学院，湖南长沙410075)

1 工程概况

衡阳耒河大桥是一座京广上行铁路改造桥梁，是一座六跨预应力混凝土连续梁桥，全长(36+4×64+36)=即828 m，由中铁第四勘察设计院设计，全桥每个T构为8个对称浇注梁段，中支点0号梁段长度9 m，悬臂梁段长度分成3．0 m和3．5 m，合龙段长2．0 m，边跨现浇段都是5．6 m，梁体各控制断面梁高分别为:端支座处及边跨直线段和跨中处为3．05 m，中支点处梁高为5．2 m，梁底下缘按圆曲线变化，圆曲线半径 R=206．337 m，箱梁顶宽13．5 m，箱梁底宽 6．4 m，在中支座 3．2 m 范围内和边支座2．8 m范围内加宽到6．9 m，为单箱单室，变高度，变截面结构。全桥在端支点，中支点，跨中设置共11道横隔梁，横隔梁处设进入孔，供检查人员通过，箱梁横截面为单箱单室直腹板，顶板厚中跨 44．5 cm，支座处 54．5 cm，腹板厚分别为45，60和80 cm，底板厚由跨中的45 cm按圆曲线变化至中支点梁根部的80 cm，纵向预应力束规格有15－7￠5与12－7￠5共2种，预应力管道摩阻系数为0．23，管道偏差系数取0．0025，耒河大桥总体布置图见图1所示，典型截面尺寸见图2和图3。

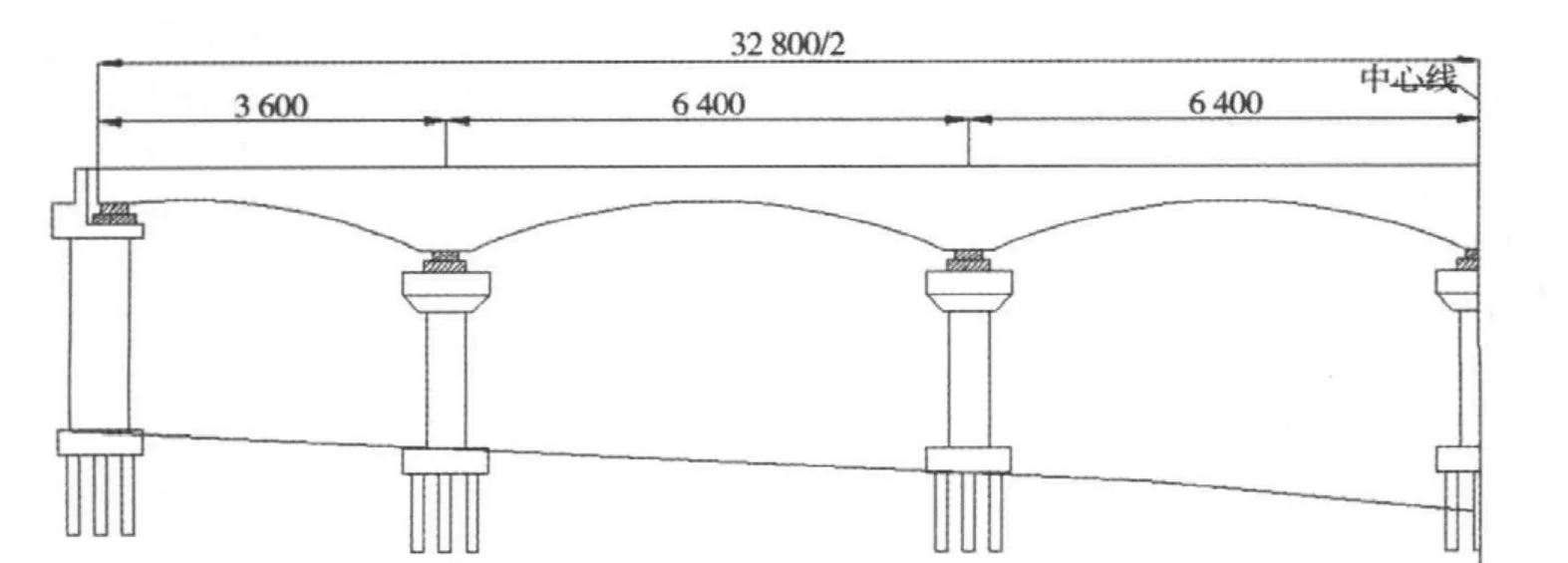
图1 耒河大桥布置图Fig．1 Arrangement diagram of lei he bridge

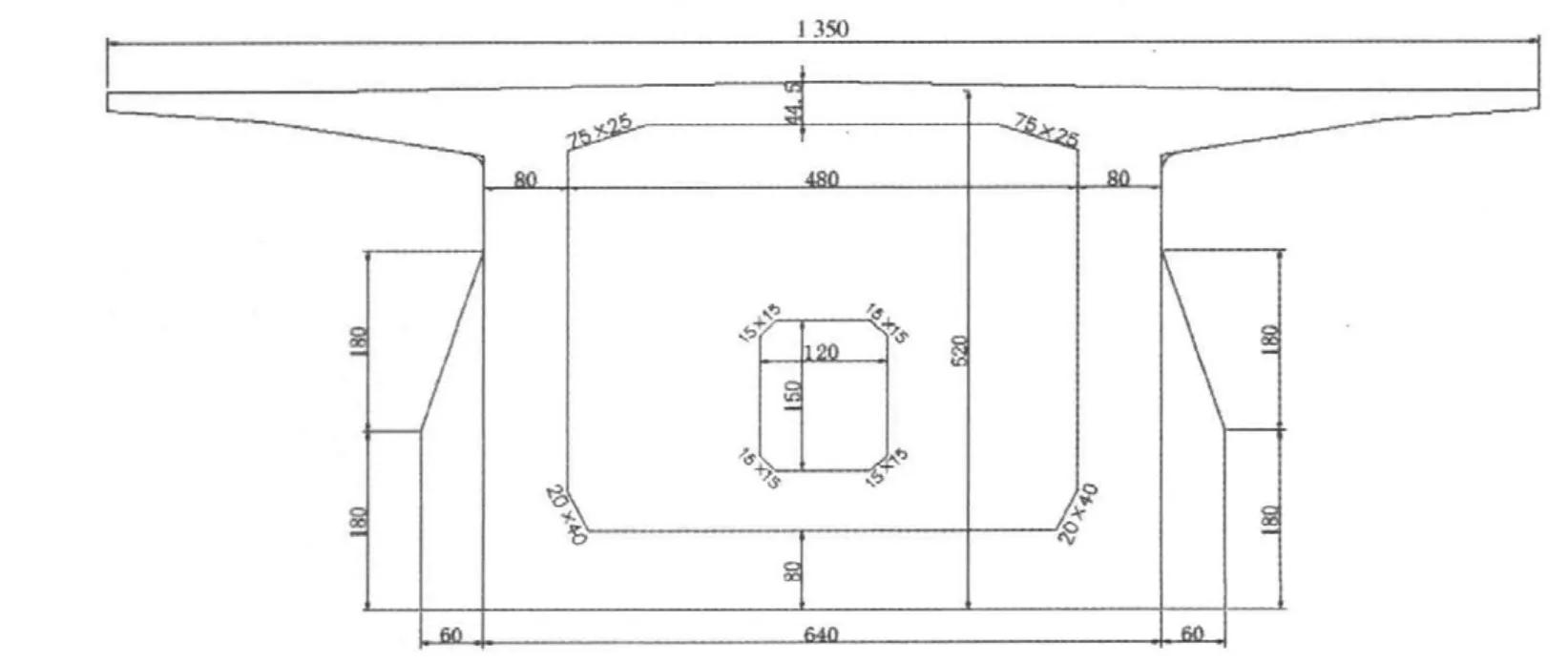
图2 跨中截面(cm)Fig．2 cross－ section of midspan

图3 支座处截面(cm)Fig．3 cross－section of support

2 合龙段施工顺序

不同桥梁合龙段施工顺序，将引起不同的施工内力，甚至结构内力再分配效应。因此，影响结构的恒载内力分布是否合理，主要看桥梁合龙段施工顺序是否适当［1］。另外，施工单位根据合龙段施工的施工组织安排，以满足各墩相应的匹配进度。桥梁的设计和现场施工的具体情况有一些差距，到了合龙施工阶段，这种差距累积是相当大的，这些问题都需要在合龙段的施工中得到适当解决。总之，成熟的合龙技术是桥梁建造成功的前提。而合龙段的施工顺序也是合龙段的重要决策之—。本文为了探讨合理的施工合龙顺序比较了4种不同的合龙顺序，分别是:(1)先边跨后次中跨最后中跨;(2)先边跨再中跨最后次中跨;(3)先中跨再次中跨最后边跨;(4)先中跨后边跨最后次中跨，从而使桥梁由T形的静定悬臂状态渐渐的成为超静定状态，实现体系转换，全桥悬臂浇筑合龙方案见图4～7。

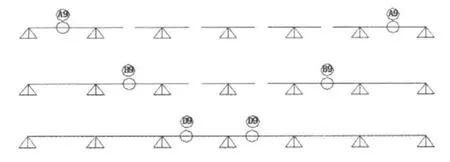
图4 合龙方案1Fig．4 Closure program 1

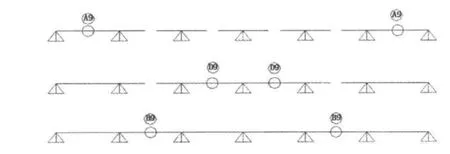
图5 合龙方案2Fig．5 Closure program 2

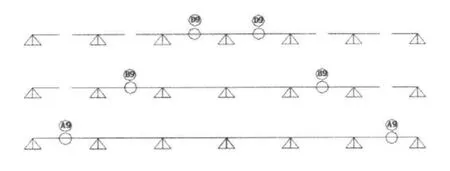
图6 合龙方案3Fig．6 Closure program 3

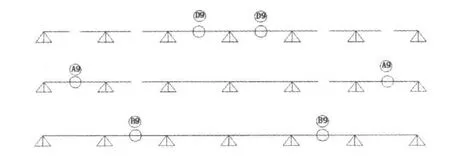
图7 合龙方案4Fig．7 Clo4sure program 4

3 合龙方案的对比

悬臂施工的连续梁由于合龙次序的不同而有不同的施工内力分布，因此，可以通过优化合龙次序来使梁成桥时的受力状态更加合理。在进行各种体系转换方案的比选时，应综合考虑施工最终合龙后的恒载内力分布情况、最大累计变形等，进行全面比较后确定合理的合龙方案。根据施工步骤，对梁体施工过程进行仿真分析，比较分析本桥上述4种初步合龙方案的几项内力和最大累积变形进而指导施工或者考虑实际施工条件进行必要合理变更。

采用MIDAS有限元软件分别按照本桥4种合龙施工顺序建立梁单元有限元模型，耒河大桥有限元模型主要包括主梁、支座约束(包括临时约束)、预应力钢束，全桥共126个单元、158个节点，计算成桥时各跨在短期效应组合(恒载+预应力+0．7活载)作用下最大跨中截面底板应力和各跨在承载能力下最大累计变形，有限元模型见图8所示。混凝土的徐变系数按JTGD 62—2004(《公路钢筋混凝土及预应力混凝土桥涵设计规范》)［2－3］取用，计算结果见表1和表2。

图8 有限元模型Fig．8 Finite element model

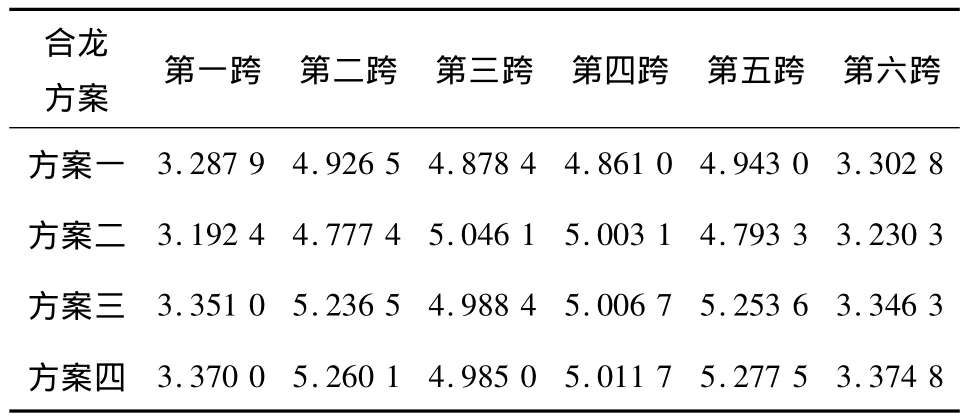
表1 跨中底板压应力Table 1 Pressure stress of slab bottom in midspan MPa

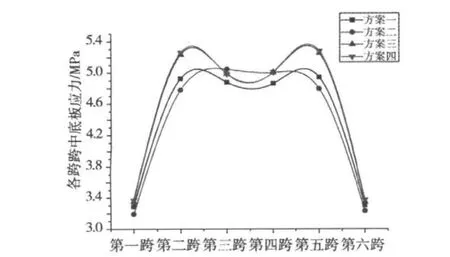
图9 各跨跨中底板应力Fig．9 Pressure stress of slab bottom in midspan

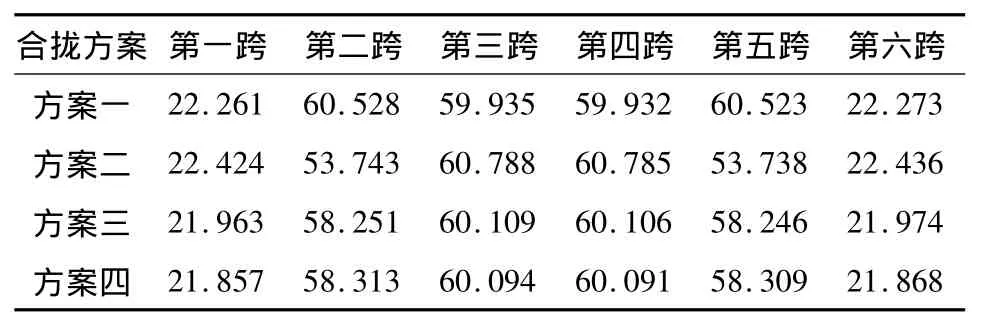
表2 最大累计位移Table 2 Maximum deflection mm

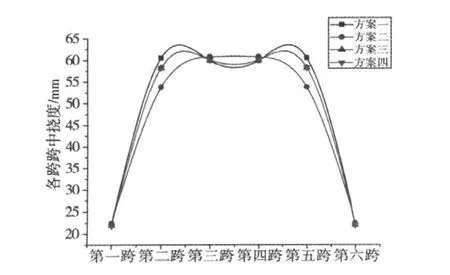
图10 各跨跨中挠度Fig．10 the deflection of the central span

通过计算分析，对比方案一到方案四，从表1～2以及图9～10，可见:方案一到方案四边跨和中跨挠度变化都不大，只有方案二次中跨挠度比其他3种方案的次中跨挠度都小。所以，从跨中挠度来看方案二也就是设计方案比其他3种方案都有优势，从图2－3也可以看出方案二的跨中挠度也比其他3种方案更合理，对于应力结果，由表1和图9可知4种方案的底板压应力都比较接近，由于是短期组合作用下的最小压应力，所以，压应力储备也足够，符合设计要求，综合考虑合龙后的挠度以及压应力储备来说设计方案二也就是先边跨再中跨最后次中跨的方案较另外3种方案更合理。通过对耒河大桥合龙顺序的不同分析可以得出:不同的合龙顺序导致结构结构体系转换时间、受混凝土收缩徐变影响时间、受合龙钢束张拉所产生的挠度均不相同，因此，结构位移和结构应力都不同且位移相差较大。通过优化合龙施工顺序可以减少后期挠度，能保证合龙的精确性。

4 初次加载龄期对后期挠度的影响

混凝土的收缩徐变对桥梁结构的影响大且持续时间长［4］，影响混凝土的收缩徐变的因素很多，归纳起来就是外部因素和内部因素的影响，初始加载龄期是外部因素的一种。混凝土徐变随加载龄期的增长而单调地衰减，又随着加载持续时间的增加而单调地增加，但增加的速度随时间的增加而衰减［5］。利用桥梁空间有限元分析软件MIDAS建立耒河大桥梁单元有限元模型，考虑混凝土加载零期为3，5，7和10 d这4种工况作用下，桥梁成桥后在预拱度组合(恒荷载+钢束预加力+徐变收缩+1/2活载)作用下各跨跨中的挠度，在预拱度组合作用下各跨位移都是往上拱，成桥后在徐变和收缩作用下会使桥梁跨中会越来越往上拱，为了防止徐变收缩对桥线型的影响，需要在施工中设置预拱度以保证行车线型，以免桥梁发生上拱破坏。对于收缩徐变计算关键是确定混凝土徐变系数，目前对于混凝土徐变分析主要依据徐变预测模型，目前国内外有很多的预测模型［6－9］，本文采用我国 JTG D62—2004(《公路钢筋混凝土及预应力混凝土桥涵设计规范》)模型［10］，不同加载龄期徐变系数见图11。

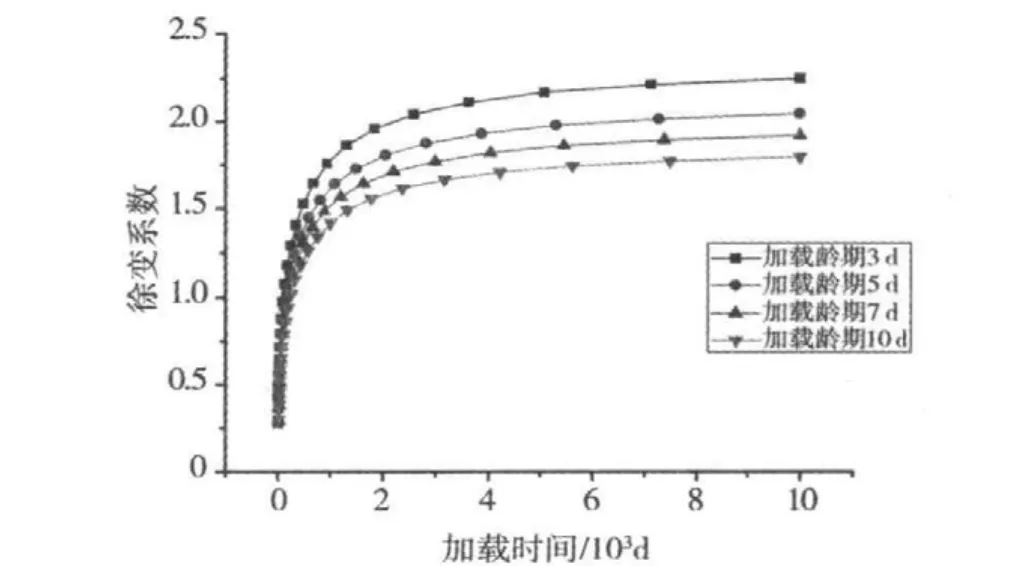
图11 C50混凝土加载10年过程徐变系数变化曲线Fig．11 the creep coefficient curves of C50 concrete load 10－year

工况一:桥梁施工时混凝土初次加载龄期为3 d。按工况一施工成桥后，考虑桥梁各跨在竣工成桥状态下，以及考虑成桥3 a、成桥10 a的跨中挠度见表3。

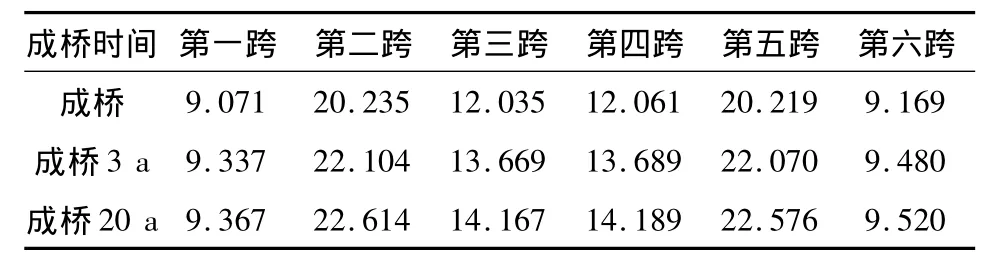
表3 工况一下各跨跨中挠度Table 3 Deflection of the central span in program 1 mm

工况二:桥梁施工时混凝土初次加载龄期为5 d。按工况二施工成桥后，考虑桥梁各跨在竣工成桥状态下，以及考虑成桥3年，成桥10年的跨中挠度见表4。

表4 工况二下各跨跨中挠度Table 4 Deflection of the central span in program 2 mm

工况三:桥梁施工时混凝土初次加载龄期为7 d。按工况三施工成桥后，考虑桥梁各跨在竣工成桥状态下，以及考虑成桥3 a、成桥10 a的跨中挠度见表5。

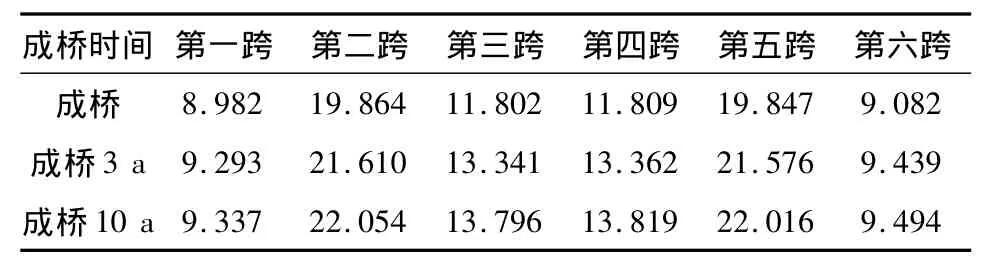
表5 工况三下各跨跨中挠度Table 5 Deflection of the central span in program 3 mm

工况四:桥梁施工时混凝土初次加载龄期为10 d。按工况四施工成桥后，考虑桥梁各跨在竣工成桥状态下，以及考虑成桥3 a、成桥10 a的跨中挠度见表6。

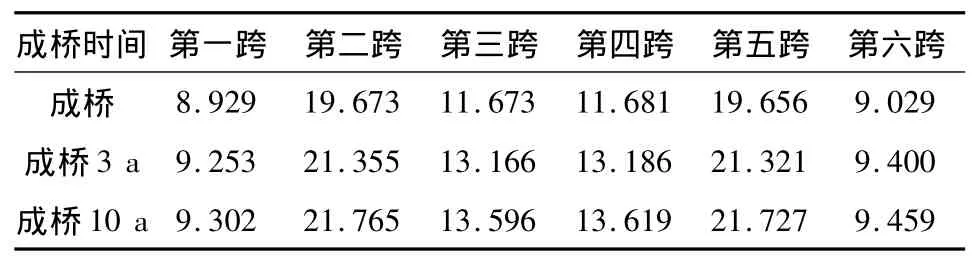
表6 工况四下各跨跨中挠度Table 6 Deflection of the central span in program 4 mm

对比表3～6的各跨跨中挠度以及图12～14可知:各个工况在竣工成桥状态下相比成桥3 a和成桥10 a的挠度要小，说明混凝土徐变收缩在成桥运营状态下仍然在缓慢发生，成桥3 a和成桥10 a在加载龄期为3，5，7和10 d时挠度变化相差不大，表明混凝土桥梁的收缩徐变基本上在3 a之内便已经完成。通过比较在4个工况作用下边跨，中跨，次中跨在成桥状态下，成桥3 a、成桥10 a的挠度，考虑到耒河大桥的对称只取3跨，如图12～14所示。由于最后合成的次中跨不管初始加载龄期是3，5，7和10 d，次中跨的挠度都比边跨和中跨大，加载龄期为3 d时，多跨连续梁桥成桥后，随着时间推移，挠度最大;加载龄期为10 d时，多跨连续梁桥成桥后，随着时间推移挠度最小;加载龄期为5～7 d时，多跨连续梁桥成后挠度鉴于两者之间，随着加载龄期时间的延长，耒河大桥桥成桥后跨中上挠的现象逐渐缓解。由此看出适当延长混凝土加载龄期对减小徐变收缩效应有一定作用的，由于施工现场采用的都是早强混凝土，这就需要通过试验确定合理的加载龄期来减少后期挠度。

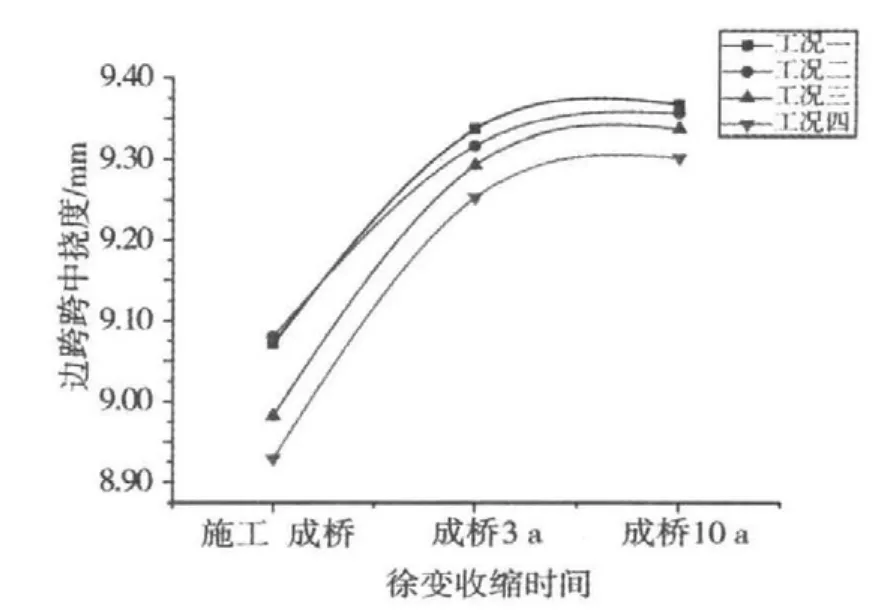
图12 边跨跨中挠度Fig．12 the deflection of side span

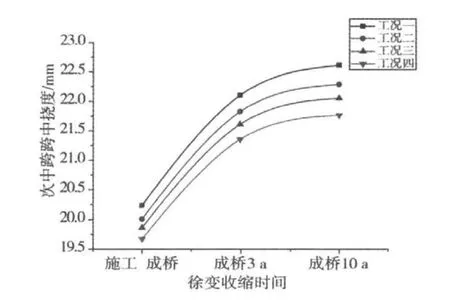
图13 次中跨跨中挠度Fig．13 the deflection of the second span

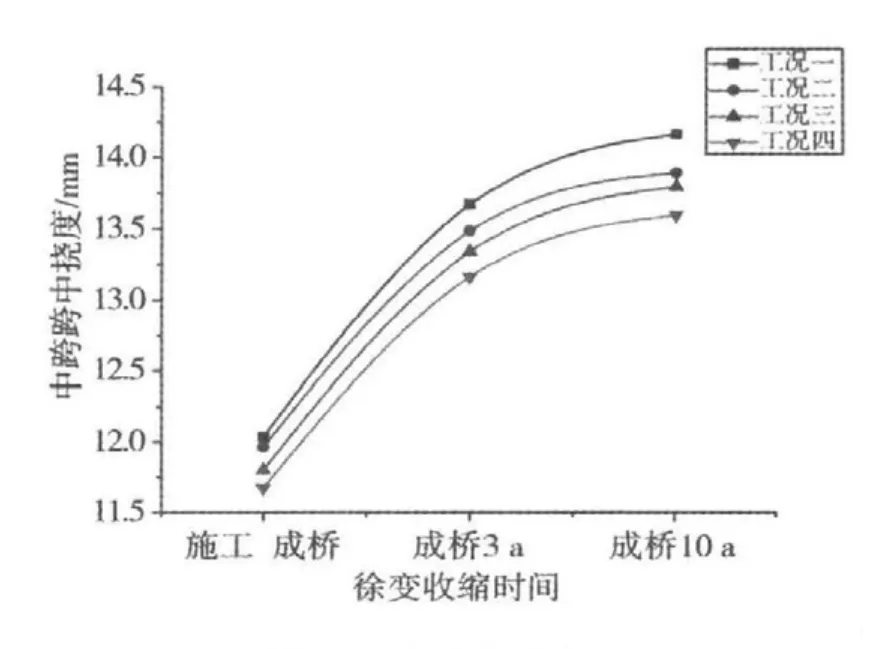
图14 中跨跨中挠度Fig．14 the deflection of the central span

5 结论

(1)多跨连续梁合龙成桥，不同的合龙顺序，使得成桥后结构的内力也有较大的差别。若预应力混凝土连续梁合龙后，结构的内力分布均匀，且对于抵消成桥后活载作用及因混凝土徐变而引起的梁体挠度有较大的压力安全储备，则认为该合龙方案最好。通过对耒河大桥合龙顺序的不同分析可以得出:不同的合龙顺序导致结构结构体系转换时间、受混凝土收缩徐变影响时间、受合龙钢束张拉所产生的挠度均不相同，因此，结构位移和结构应力都不同且位移相差较大。通过优化合龙施工顺序可以减少后期挠度，能保证合龙的精确性。

(2)徐变收缩对混凝土桥梁的影响时间跨度长，而且与结构形式、材料特性以及施工方法等因素有关。反映在以悬臂浇筑法施工的大跨度连续混凝土箱梁桥上，从梁段悬臂浇筑一开始，徐变就开始了对桥梁结构产生了影响。悬臂施工混凝土的初始加载龄期对是影响徐变收缩的1个因素，加载龄期为3 d时，多跨连续梁桥成桥后，随着时间推移挠度最大;加载龄期为10 d时，多跨连续梁桥成桥后，随着时间推移挠度最小;加载龄期为5～7 d时，多跨连续梁桥成后挠度鉴于两者之间，随着加载龄期时间的延长，耒河大桥成桥后跨中上挠的现象逐渐缓解。由此看出适当延长混凝土加载龄期对减小徐变效应是有一定作用的，由于施工现场采用的都是早强混凝土，这就需要通过试验确定合理的加载龄期来减少后期挠度。

［1］范立础．预应力混凝土连续梁桥［M］．北京:人民交通出版社，1998．FANLichu．Prestressed concrete continuous beam bridge［M］．Beijing:People＇s Communications Press，1998．

［2］JTG D60—2004，公路桥涵设计基本规范［S］．JTG D60—2004，General code for design of highway bridges and culverts［S］．

［3］JTG D62—2004，公路钢筋混凝土及预应力混凝土桥涵设计规范［S］．JTG D62—2004，Code for design of highway reinforced and prestressed concrete bridges and culverts［S］．

［4］郭玉峰．大跨度混凝土连续梁收缩徐变对预拱度设置影响研究［D］．武汉:武汉理工大学，2009:5—2．GUOYufeng．Research of the influence of large－span continuous concrete bridge creep on setting camber［J］．Wuhan:Wuhan university of technology，2009:5—2．

［5］熊维．不同强度早龄期混凝土徐变及徐变对长期荷载作用下预应力构件的影响［D］．天津:天津大学，2011:4—25．XIONG Wei．Different early － age strength of concretecreep and creep under load for long－term effects of prestressed beamMaster degree thesis［D］．Tianjing:Tianjing University，2011:4—25．

［6］杨小兵．混凝土收缩徐变预测模型研究［D］．武汉:武汉大学，2004．YANG Xiaobing．Research on prediction model of concrete shrinkage and creep［D］．Wuhan:Wuhan university，2004．

［7］Mcdonald D B，Roper H．Accuracy of predication models for shrinkage of concrete，ACI Materials Journal，May －June 1993:265－271．

［8］Bazant Z P．Improved prediction model for time－dependent deformations of concrete:Part 2 － Basic creep［J］．Materials and Structures，1991(24):409 －421．

［9］ Bezant Z P，Baweja S．Justification and refinements of Model B3 for concrete creep and shrinkage 1．Statistics and sensitivity［J］．Materials and Structures，1995(28):415－430．

［10］张汉一．徐变对大跨度预应力混凝土连续箱梁桥施工线形控制的影响［J］．铁道科学与工程学报，2012，9(4):14－18．ZHANG Hanyi．Effect of creep on the construction of linear control of large－span prestressed concrete continuous box beam bridge［J］．Journal of Railway Science and Engineering，2012，49(1):14 －18．