大秦重载铁路运输系统供需匹配优化模型＊

陈维亚，陈治亚，麻欢，冯芬玲

(1．中南大学交通运输工程学院，湖南长沙410075;2．中南大学 信息科学与工程学院，湖南长沙410083)

重载铁路运输是铁路货运发展的方向之一。重载铁路运输专线在我国大宗货物运输中发挥着越来越重要的作用。大秦铁路作为一条非常重要的重载运煤专线，近年来随着运输装备和管理水平的不断提高，运输能力得到很大的提高［1］，但是相对于煤炭需求总量的不断增长和煤炭需求结构的变化，大秦铁路的运力资源仍显紧张。一方面，在保证运输安全的基础上为了充分利用现有运输能力和提高运输设备的利用率，大秦铁路仍很大程度上用“以运定产”的模式来制定和执行生产计划［2］;另一方面，为了应对煤炭市场需求结构的变化，大秦铁路正不断加强“路港矿”协同环境，尽最大程度做到煤炭生产、运输与市场需求的匹配，减少供需不均衡对资源的浪费［3］。近年来，对于重载铁路运输系统的运输组织优化研究，大部分集中在重载运输装车区(或基地)车流组织优化方面。文献［4］通过分析组织始发直达列车的必要条件及参数选择，构造了装车地列车编组计划的非线性0－1规划模型，并给出了始发车流的各种组合开行方案。文献［5］针对基地直达车流组织优化问题，通过分析基地直达列车开行的条件和各种费用消耗，构建了以总换算车小时消耗最小为目标函数的基地直达车流组织优化的非线性0－1规划模型。文献［6］通过分析装车地组织直达运输的各种费用消耗，综合考虑运输网络中的径路选择和重载运输通道端点换重情况，构建了装车地直达运输组织方案优化模型。文献［7］以大秦重载铁路运输为研究对象，重点基于湖东站的作业组织，构建了以直达运输节省改编时间最大化为目标的重载运输装车区车流组织模型。文献［8］根据我国重载铁路车流组织的特点，针对开行组合重载列车和单元重载列车的重载铁路装车区车流组织优化问题，建立了以组合时间耗费最小化和重载通道流量最大化为目标的重载铁路装车区车流组织优化模型。随着铁路信息化程度的提高，对重载铁路运输系统的运输组织优化正逐步拓展为基于多方信息共享的集疏运一体化协同优化。本文通过分析大秦重载铁路运输系统的特点，根据市场运输需求以及大秦铁路集疏运系统的各种能力约束等建立运输供需匹配优化模型，在“路港矿”信息共享机制［9］下对“集疏运”的深度衔接和“路港矿”的一体化协同进行优化。

1 问题分析

大秦重载铁路运输系统承担专线煤炭运输任务，其一端处于线路上游的煤炭货源地，装车点分布在集运干支线上，另一端是线路下游的煤炭消费地或转运港口，通过直达运输到达消费地或转运港口的卸车区，形成封闭的树型重载铁路集疏运一体化系统。与普通铁路运输相比，大秦铁路重载运输系统具有如下特点:(1)大秦铁路是一个树型的网络结构(如图1所示)，树的根须是多装车端，树的枝叶是多卸车端;(2)大秦铁路是整列装车、整列运输、整列卸车、整列回空。根据牵引重量以及组合方式将列车分为单元5 000 t、单元1万t、组合1万t、组合2万t等类型;(3)采用固定车底循环直达运输方式组织列车重去空回;(4)大秦铁路一般都采用大轴重的C80货车。

图1 大秦铁路树型网络示意图Fig．1 Tree － like network of Daqin railway transportation system

目前，影响大秦铁路运输供需匹配的因素比较复杂。在运输供给方面，主要受固定车底工作量、装车点的能力、卸车点的能力、区间的通过能力、中间站的通过能力、组合分解站的通过能力等各种能力的约束;在运输需求方面，主要受运输需求的多样性及其重要程度的影响。运输需求多样性主要表现为装车点、卸车点、路径、煤炭品类、列车需求数量、运输时间等多属性的不同组合，且每个运输需求的重要程度不同。在实际运输过程中通常需要根据以下各项原则运用综合评价方法确定运输需求的综合重要程度:

(1)重点需求优先原则。如优先满足重点发电企业的电煤运输需求。

(2)应急需求优先原则。当需求企业的生产因某种煤的库存不足而受到严重影响时，优先安排此种煤的运输。

(3)旺盛需求优先原则。优先安排市场需求大的煤炭运输，以防止煤炭压港和减少列车的在站停留时间。

(4)时间顺序优先原则。根据需求企业要求的运输发到时间顺序来分配运输资源。

(5)先提先服务原则。在其他条件都相同的情况下，先提出的运输需求先安排运输。

因此，本文的研究问题是在考虑大秦重载铁路的树型结构和运输能力受到约束的情况下，如何根据运输需求重要性为市场上多样性的运输需求合理地分配运输供给，使得大秦重载铁路集疏运系统的供需匹配最优。

2 模型建立

2．1 模型假设

根据以上描述，此类供需匹配问题比较复杂。因此，根据当前大秦重载铁路运输系统的技术装备和运输组织技术对模型进行以下假设:

(1)以5 000 t列车为1个基本单位，1万t列车可以折算成2个基本单位，2万t列车可以折算成4个基本单位;

(2)所有客户提出的运输需求都是整数;

(3)以某一时间单元为周期进行供需匹配;

(4)在树型网络中，1个装车点到1个卸车点的路径只有1条，不考虑路径选择;

(5)假设所有货车都是C80，不需考虑车种别;

(6)运输需求在不断变化，已经提报的运输需求的完成情况将对未来的运输供给产生影响，因此运输需求及其综合重要程度可以进行动态调整;

(7)由于机车、车辆、线路等需要检测维修，各种能力约束将动态更新。

假设(6)和(7)中所需的信息将随着大秦重载铁路运输系统的“路港矿”信息共享平台的建立和付诸实施而得以实现。

设i代表装车点，装车点总数为I;j代表卸车点，卸车点总数为J;k代表煤炭的类别，第i个装车点煤的类别总数为Ki;q代表车站，车站总数为Q;a代表区间，区间总数为Q－1;Pij为装车点i到卸车点j的路径;Dijk为装车点i到卸车点j对煤种k的运输需求;Sijk为分配给运输需求Dijk的运输供给;wijk表示运输需求Dijk的综合重要程度;Cv表示列车的工作量;Cil表示装车点i的装车能力;Cju表示卸车点j的卸车能力;Ca表示区间a的通过能力;Csq表示车站q的通过能力;σija表示区间a归属于路径Pij的状态值，归属时为1，否则为0;θijq表示车站q归属于路径Pij的状态值，归属时为1，否则为0。

2．2 目标函数

在实际的运输过程中，由于分配的运输供给不会大于运输需求，因此，为了使大秦铁路的供需匹配程度达到最大，在优先满足重要运输需求的情况下，运输需求与运输供给的差应尽可能小，因此，模型的目标函数为

2．3 约束条件

模型的可行解要满足以下约束条件。

分配给每个运输需求的运输供给之和不能大于列车的工作量，即

分配给每个装车点的运输供给总和不能大于该装车点的能力:

分配给每个卸车点的运输供给不能大于该卸车点的能力:

分配给每个区间的运输供给不能大于该区间的通过能力:

分配给每个车站的运输供给不能大于该车站的能力:

运输供给不能大于运输需求:

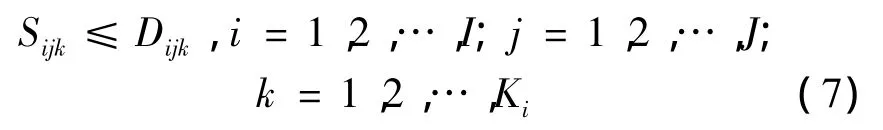
此外，根据假设，分配的运输供给必须满足非负约束和整数约束:

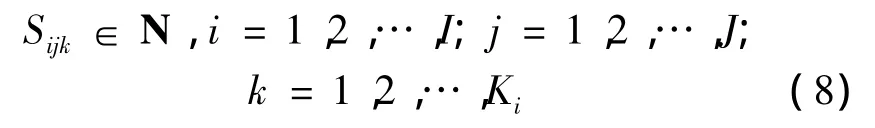
2．4 模型转换

通过综合分析模型的目标函数和约束条件，可以将模型进一步转换为考虑运输需求重要性的运输供给最大化模型:

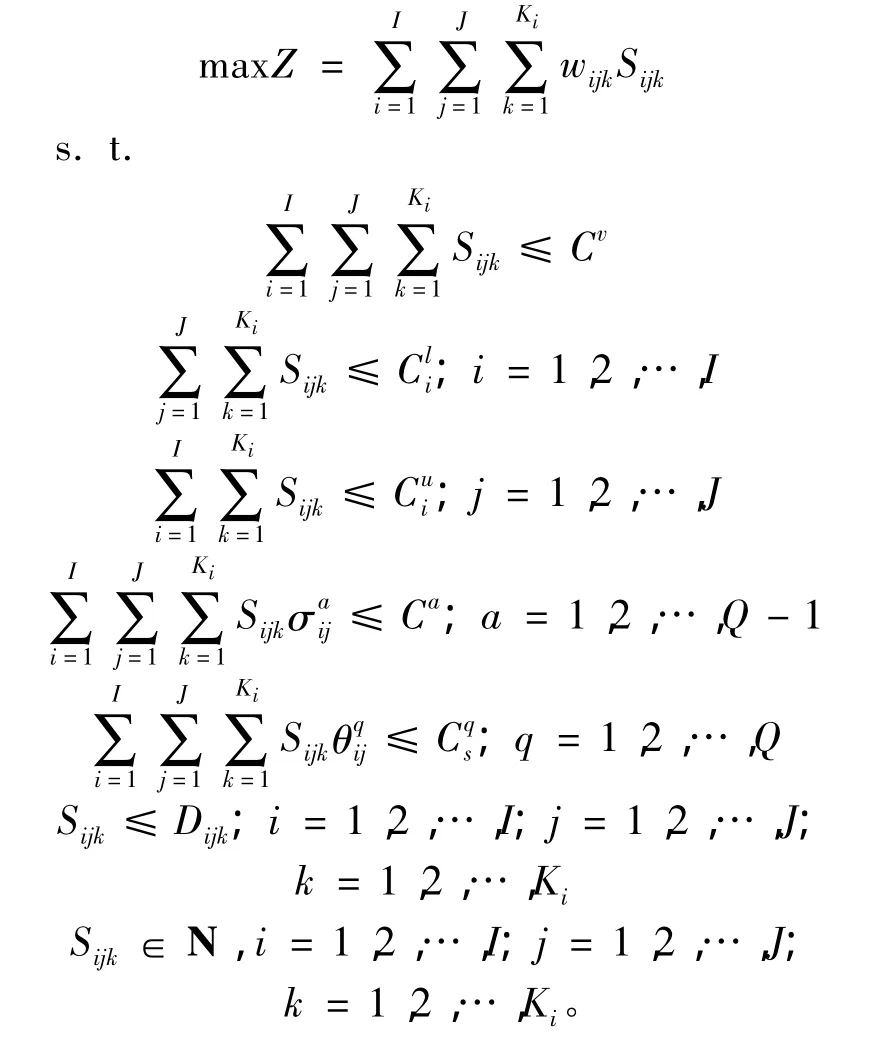
3 模型求解算法

通过观察上述数学模型，可以发现转换后的模型具有如下特点:模型的目标函数是求极大值;约束条件中决策变量的系数取值为1或0;除了非负约束和整数约束之外，其余约束条件都是“≤”的不等式;约束条件右端的常数都是整数。因此，这是一个整数线性规划模型，利用已有的分支定界法以及割平面法等都可以求解该模型［10］。但是，由于整数线性规划问题是一个NP难问题，计算复杂性将随着问题规模的增大而迅速增加，所花费的代价也将难以接受。但是，注意到问题的变量在整数范围内是连续的，约束都是能力约束。由于这样的特殊性，本文采用对综合重要程度最大的运输需求优先分配运输供给的贪心选择策略对问题进行求解。算法步骤如下。

第1步:数据初始化。

第2步:运用灰色综合评价方法［11］计算综合重要程度wijk，然后将wijk按照从小到大的顺序进行排序。

第3步:找出最大的wijk所对应的Sijk，找出与Sijk相关的约束条件。

第4步:从与Sijk相关的约束条件右端常数中找出最小值，并赋值给Sijk，然后将相关的约束条件右端常数减去相应的数值。

第5步:从剩余的综合重要程度中找出最大的wijk，重复以上第3和第4步，直到最后所有的Sijk都被赋值，没有权重剩余。

第6步:输出结果，结束。

该贪心选择算法求得的解就是问题的最优解，证明如下。

证明:如果所有运输需求都能被满足，贪心选择算法所求得的目标函数(1)的值为0，显然就是最优解;否则，运输供给能力将达到最大，此时，贪心选择算法求得的解为如下形式:若某个运输供给，则满足的所有运输供给一定是满负荷运输。假设该解不是最优解，则存在某个运输供给，以及存在所对应的不是满负荷运输，则把一个单位的换成一个单位的可以得到更优解，则假设不成立，故贪心选择策略能求得问题最优解。证毕。

算法的第1步的排序计算量为O(m*logn)，算法的第3步到第5步是一个循环过程，其计算量为O(m*n)(其中n表示变量的个数，m表示约束条件的个数)，故整个算法的计算时间为O(n*logn+m*n)。由于 logn＜＜m，因此O(n*logn+m*n)=O(m*n)，算法的计算时间为O(m*n)。由此可见，该算法的主要计算量在于算法的第3步到第5步。

4 算例分析

基于大秦铁路集疏运系统的复杂性和大秦铁路集疏运“路港矿”信息共享平台还未付诸实施，模型所需的各种数据难以收集，因此，为了验证模型的可行性和算法的有效性，本文用2个装车点、2个卸车点、2个车站、5个区间组成的简单树型网络(如图2所示)进行算例分析。

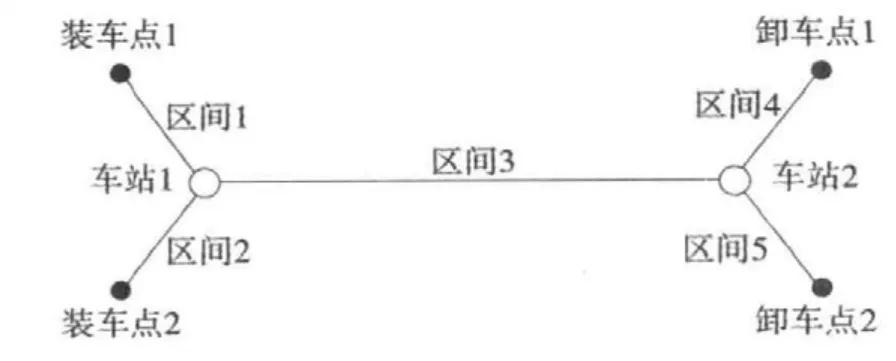
图2 算例树型网络示意图Fig．2 Example tree－ like transport network

表1 区间和车站的路径归属状态取值Table 1 0－1 values of the sections and the stations of the paths 和

表1 区间和车站的路径归属状态取值Table 1 0－1 values of the sections and the stations of the paths 和

区间或车站 路径P11 P12 P21 P22区间11100区间2 0 0 1 1区间3 1 1 1 1区间4 1 0 1 0区间5 0 1 0 1车站1 1 1 1 1车站21111

在算例中，假设每个装车点都有2种煤炭需要运输，每个卸车点也都需要这2种煤炭，则一共有2×2×2=8种运输需求。每个运输需求及综合重要程度如表2所示，而给定的各种运输能力如表3所示。

表2 各运输需求及其重要性的权值Table 2 Volumes and significance of the transport demand

表3 各装卸车点、车站和区段的能力和列车工作量取值Table 3 Capacity of the loading/unloading spots，the stations and the sections and the train work volume

表2中的运输需求的综合重要程度由灰色综合评价方法求得并按百分制进行取值，分数越高，表示运输需求越重要，反之，则运输需求越不重要。

利用Matlab对求解算法进行编程，计算得到为每个运输需求分配的运输供给和未满足的运输供给(如表4所示)。

由表2和表4可以看出:该模型和算法根据运输需求的重要程度进行运输供给分配，使运输供给和运输需求得到较好地匹配。对于未满足的运输需求，将在下一次的运输供给分配过程中根据新的运输需求重要程度得到重新调整和分配。另外，通过模型和算法还计算出各种能力的剩余值，如表5所示。

表4 分配的运输供给和未满足的运输需求Table 4 The used transport supply and the unsatisfied transport demand

表5 各种能力的剩余值Table 5 The remaining Capacities

从表5可以看出:分配的运输供给都没有超过各种能力，说明没有出现列车在车站停车等待、煤炭待卸压港和等待装车现象。而且通过观察各种能力剩余值，还可以发现运输瓶颈，为有针对性的采取改进措施提供决策依据。比如C1u的剩余值为0，说明该卸车点的能力完全被利用，可以通过改扩建煤炭堆场或加快煤炭疏解出港等措施来提高卸车能力。

5 结论

在分析大秦重载铁路集疏运系统的特点的基础上，考虑客户运输需求重要性和大秦铁路树型运输系统的能力约束，构建了大秦重载铁路集疏运系统的运输供需匹配优化模型，并设计了基于贪心选择策略的求解算法，算例分析证明了模型和算法的合理性和有效性。该模型和算法可直接用于大秦铁路重载运输系统，在“路港矿”信息共享平台建立实施后发挥作用，并可用于类似大秦铁路树型结构的重载运输系统的供需匹配优化。

［1］耿志修．大秦铁路重载运输技术［M］．北京:中国铁道出版社，2009．GENG Zhixiu．Daqing heavy haul railway transportation technologies［M］．Beijing:China Railway Press，2009．

［2］安路生．中国铁路运输新实践［M］．北京:中国铁道出版社，2009．AN Lusheng．Innovative practice of China railway transportation［M］．Beijing:China Railway Press，2009．

［3］冯芬玲，陈治亚，雷志鹏．铁路重载运输集疏运一体化的协同学动因及实践［J］．铁道运输与经济，2009，32(8):25－29．FENG Fenling，CHEN Zhiya，LEI Zhipeng．The synergic motivation and practice of integrated collection－transport－distribution in heavy－haul railway transportation［J］．Railway Transportation and Economy，2010，32(8):25－29．

［4］林柏梁，朱松年，史德耀，等．装车地直达列车编组计划的优化模型［J］．中国铁道科学，1995，16(2):108－114．LIN Boliang，ZHU Songnian，SHI Deyao，et al．The optimal model of the direct train formation plan for loading area［J］．China Railway Science，1995，16(2):108 －114．

［5］曹学明，林柏梁，刘晗，等．基地直达车流组织优化［J］．铁道学报，2007，29(1):16－22．CAO Xueming，LIN Boliang，LIU Han，et al．Optimization of car flow organization in nonstop train loading base［J］．Journal of the China Railway Society，2007，29(1):16－22．

［6］强丽霞．基于端点换重的装车地直达车流组织优化模型与算法研究［J］．铁道学报，2009，31(6):91－96．QIANG Lixia．Model and algorithm of optimized organization scheme for through trains from loading points based on endpoint－ for－ weight［J］．Journal of the China Railway Society，2009，31(6):91－96．

［7］唐保刚．重载运输装车区车流组织的研究与探讨［D］．北京:北京交通大学，2009．TANG Baogang．Study on the organization of wagon flow in the heavy haul loading area［D］．Beijing:Beijing Jiaotong University，2009．

［8］赵鹏，张进川，唐宝刚．基于组合列车的重载铁路装车区车流组织优化模型研究［J］．中国铁道科学．2010，31(6):116－121．ZHAO Peng，ZHANG Jinchuan，TANG Baogang．Study on the optimization model of car flow organization in the loading area of heavy haul railway based on the combined trains［J］．China Railway Science，2010，31(6):116 －121．

［9］Chen W．Information sharing framework for the integrated collaborative operation in through transport of railway freight［J］．Applied Mechanics and Materials，2013，(253):1213－1217．

［10］夏伟怀，符卓．运筹学［M］．长沙:中南大学出版社，2011．XIA Weihuai，FU Zhuo．Operation research［M］．Changsha:Central South University Press，2011．

［11］袁嘉祖．灰色系统理论及其应用［M］．北京:科学出版社，1991．YUAN Jiazu．The theory and application of grey system［M］．Beijing:Science Press，1991．