槽型断面斜拉桥塔梁墩固结区应力的数值模拟＊

周敏，戴公连，粟淼

(中南大学土木工程学院，湖南长沙410075)

新建沪昆高铁与既有武广高铁相交时，为了尽可能减小建筑高度和线路纵坡，及施工过程对武广高铁正常运营的影响，采用转体施工塔梁墩固结结构体系槽型断面独塔斜拉桥，跨越武广高铁。本桥塔梁墩固结区结构、受力均相当复杂，应力分布集中现象明显，有必要对塔梁墩固结区应力分布规律及传递途径作深入研究，用于指导结构设计，以确保其结构的合理性与安全性［1－5］。

1 工程背景

文中背景工程是新建沪昆高铁上某联络线特大桥，跨径为(32+80+112)m的单线铁路槽型断面独塔斜拉桥，采用不对称独塔双索面塔梁墩固结结构体系，主梁采用预应力混凝土槽型梁，为克服小跨侧边支座负反力，在80 m跨侧增加一孔32 m辅助跨，主塔为钢筋混凝土矩形空心截面，槽型梁边箱与桥塔融为一体，边墩及辅助墩设纵向活动支座，横向设限位挡块。该大桥跨越武广高铁，为了最大限度地缩短跨线作业时间，采用转体施工方案，利用天窗时间转体到位。桥梁总体布置如图1所示。

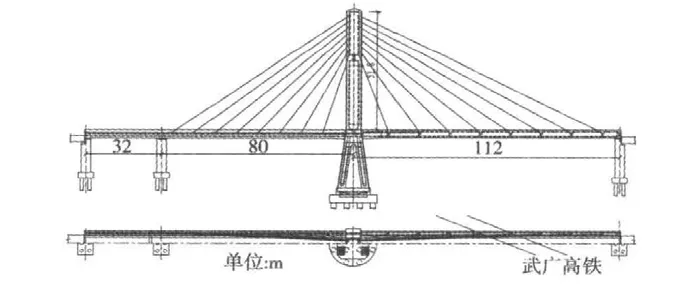
图1 总体布置图Fig．1 General arrangement of bridge

2 固结段构造及数值模拟模型

2．1 固结段构造细节

梁部采用预应力混凝土槽型梁结构形式，跨武广高铁大主跨梁高3．5 m，小主跨及边辅助墩梁高3．7 m，塔梁墩固结处局部以1/15的坡率加高到4 m，梁顶齐平。槽型梁为边箱式的槽型截面，箱高为梁高，箱宽为2．1 m，两箱中心距8．7 m，等于斜拉索横向间距。主梁横截面如图2所示。

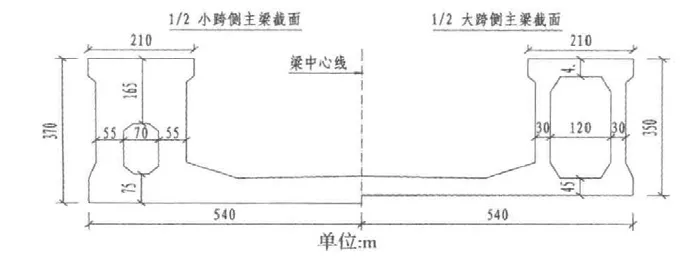
图2 主梁横截面图Fig．2 Cross－section of main beam

为减小转体质量，须尽量压缩结构尺寸，塔梁墩固结构造上没有按照一般的做法将主梁夹在桥塔内侧，而是以满足槽型梁内的铁路限界为前提尽量内收塔柱的张开度，将槽型梁的两边箱插入到塔柱中形成固结，并在梁下设有1道横梁以构成桥塔横向框架体系。固结段主梁2肢2洞，上塔柱2肢2洞，下塔柱4肢4洞，上塔柱孔洞从槽型梁的边箱顶板穿过，下塔柱孔洞从边箱底板穿过，均与槽型梁边箱孔洞交汇，总共8肢8洞，构造复杂。固结段构造如图3所示。

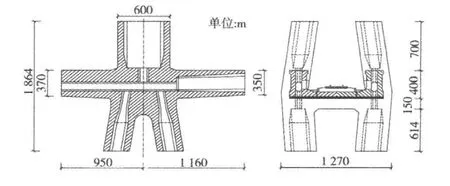
图3 固结段构造图Fig．3 Structure of consolidation segment

2．2 计算模型的建立

采用基于圣维南原理的子模型方法［6－7］，整体模型为局部模型提供边界条件。利用Midas/Civil建立整体模型对大桥进行受力分析;截取固结段利用Ansys建立局部模型，局部模型的内力和位移边界条件从整体模型的计算结果中提取;进行塔梁墩固结段局部应力分析。为了避免边界条件对固结区受力的影响，主梁、塔柱、桥墩的截取面离固结区的距离应足够长。局部分析模型横桥向计入桥梁全宽，主梁左右两端截取长度均大于2倍梁高，模型纵桥向合计长21．10 m，竖桥向合计长18．64 m。选用20个节点的solid95实体单元进行模拟，采用自由网格划分，共离散为135 188个单元，215 805个节点，网格划分后的有限元模型如图4所示。

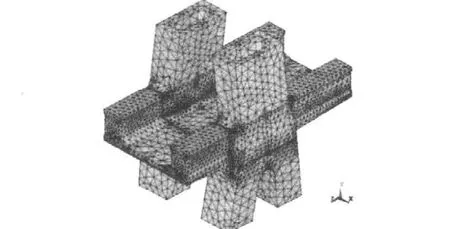
图4 局部分析有限元模型Fig．4 Finite element model of local analysis

2．3 边界条件

2．3．1 预应力的等效

局部分析模型采用等效荷载法来模拟预应力［8］。固结段共有B1(底板束)，F1～ F4(腹板束)和T1～T5(顶板束)10类钢束通过。其中:T4和T5右端锚固在模型内，左端在模型边界处被截断，其余钢束两端均在模型边界处被截断。被截断的预应力钢束，预应力效应已经包含在从整理模型中所提取的边界内力中，而锚固在模型内的预应力钢束，则需要等效成外荷载的形式作用在模型上。预应力钢束与混凝土之间产生的摩擦力当作外荷载加至模型上，才能使得力的平衡条件得到满足。预应力等效示意如图5所示。

图5 预应力等效示意图Fig．5 Prestressing equivalent schematic diagram

其中:N1为左端被截断钢束等效集中力，N2包括右端被截断钢束等效集中力和T4和T5钢束锚固集中力水平分量之和，N3为T4和T5钢束锚固集中力竖直分量之和，f为预应力钢束和混凝土之间产生的摩擦力。

2．3．2 内力边界条件

局部模型有8个切割面，施加在这8个面的位移和荷载称为边界条件。边界条件选择是否合适，直接影响到固结区的应力分析结果。经过试算，分别在主梁左端、主梁右端切面处和上端塔柱两个切面处施加内力边界条件，在下端塔柱4个切面处施加固定约束，以消除刚体位移，能够较准确地模拟固结段的边界条件。为了使荷载施加方便，在各边界截面的质心处均建立主节点，截面上其余节点与主节点之间形成刚域，边界条件均施加在主节点上。

实际的分析计算过程中，考虑了多种不同的荷载工况，本文仅就一种较不利的内力组合进行分析，探讨固结段的应力分布及传递规律。从Midas/Civil中提取的边界内力符号规定:轴力拉为正，剪力逆时针方向为正，弯矩使单元下翼缘受拉为正;Ansys中内力符号和坐标轴一致。表1中给出的是通过转换之后Ansys局部模型中内力边界条件(包含预应力效应)。

2．3．3 模型内力校核

为了保证计算结果的可靠性，对局部模型的内力进行校核。取固结区内的3个控制截面，截面1中心向左2．60 m，截面2中心向左1．25 m，截面3为固结区中心截面，对截面上的应力进行积分运算，得到截面上的内力，与整体模型提取的截面内力相比较，相对误差均在10%以内，这表明局部分析模型的计算结果是可靠的。内力校核结果如表2所示。

表1 内力边界条件Table 1 Internal force boundary conditions

3 计算结果及分析

3．1 应力计算结果

由表3和图6可知:塔梁墩固结区应力除局部小范围内超限外，其他绝大部分均能够满足规范要求。固结区主拉应力、主压应力分布情况如图6所示。

图6 固结区应力等值云图Fig．6 Stress contours nephogram of fixed region

由图6(a)可知:固结区主拉应力整体较小，分布较均匀，但固结区孔洞附近、槽型梁底上下缘及塔柱外边缘拉应力较大。由图6(b)可知:固结区主压应力整体水平较低，分布较均匀，但主梁与塔柱相交处压应力较大。

固结区应力计算结果如表3所示。应力符号规定:拉应力为正，压应力为负。

表2 模型内力校核Table 2 Model internal forces checking

表3 固结区应力计算结果Table 3 Stress results of fixed region MPa

3．2 应力集中点附近区域的应力分布

塔梁墩固结区截面突变处，应力集中现象明显，由于这些应力集中区域的应力超出规范容许值，故有必要了解这些应力最大点位置附近的应力分布情况，从而明确其影响范围，并找出它们的传递规律。压应力最大值出现在固结段左端下缘塔柱与梁体在桥面相交处，如图7中A点所示;拉应力最大值出现在固结区内部主梁顺桥向孔洞和桥塔孔洞交汇处，如图7中B点所示。

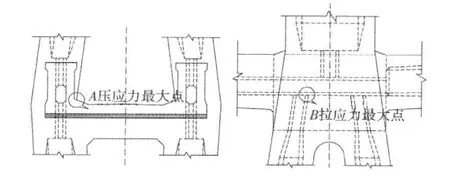
图7 应力最大值点的位置Fig．7 Location of the maximum stress points

在A点分别沿顺桥向和竖桥向截取一定长度，竖向正应力和主压应力分布如图8所示。

A点顺桥向坐标为0．39，竖桥向坐标为0。从图8可知:在A点出现最大压应力后，压应力沿着顺桥向和竖桥向方向均迅速衰减，降低到较低的应力水品之后趋于稳定，A点附近区域的应力水平处于5～13 MPa之间，远小于A点应力，说明A点出现最大应力为局部应力集中现象。

在B点分别沿顺桥向和竖桥向截取一定长度，横向正应力和主拉应力分布如图9所示。

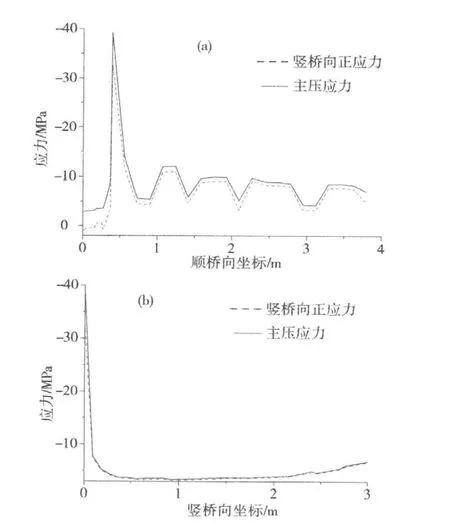
图8 A点附近区域应力分布Fig．8 Stress distribution of area near point A

B点坐标为0。从图9可知:在B点出现最大拉应力后，沿顺桥向方向，应力逐渐减小，经过一段距离拉应力稳定在3．50 MPa左右;沿竖桥向方向，应力逐渐减小，经过一段距离拉应力降低到1 MPa左右。B点出现最大拉应力仅为局部现象，但相对于最大压应力的衰减速度而言，最大拉应力附近区域应力降低速率相对缓慢，且在其周围局部范围内存在一定水平的拉应力。

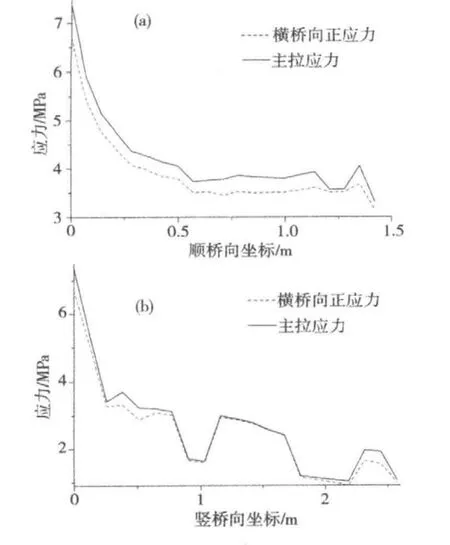
图9 B点附近区域应力分布Fig．9 Stress distribution of area near point B

3．3 截面应力的分布

选取固结区内某一主梁C截面和下端塔柱D截面(均在塔梁相交位置)，分析截面上应力沿指定路径1和路径2的分布特征。C和D截面如图10所示。

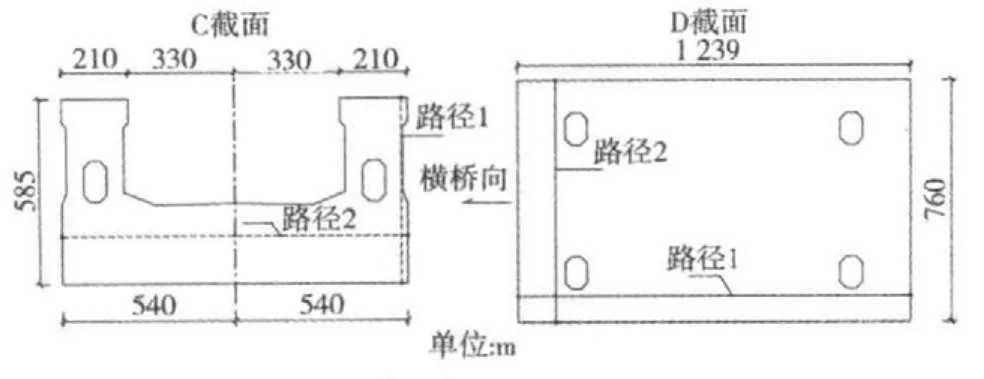
图10 C截面和D截面示意图Fig．10 Section C and D schematic diagram

C截面应力如图11所示。从图11可知:C截面应力主要分布在－10～0 MPa之间，主压应力、顺桥向正应力明显大于竖桥向、横桥向正应力及主拉应力。这主要是由于主梁受到很大的轴力引起;沿截面高度方向，正应力和主应力均在截面顶端达到最大值，分布无明显规律性;沿截面宽度方向，应力呈现两端较大中间较小的分布状态。

从图12可知:D截面应力大小主要分布在－4～1 MPa之间，主压应力、竖桥向正应力明显大于顺桥向、横桥向正应力及主拉应力，主要是由于桥塔受到很大的轴力引起;沿横桥向方向，应力呈现两端大中间小的分布状态，孔洞处(4．2 m和－4．2 m)应力有突变;沿顺桥向方向，竖桥向正应力和主压应力波动较大，孔洞处(2．3 m和－2．3 m)应力有突变，突变现象更为明显。

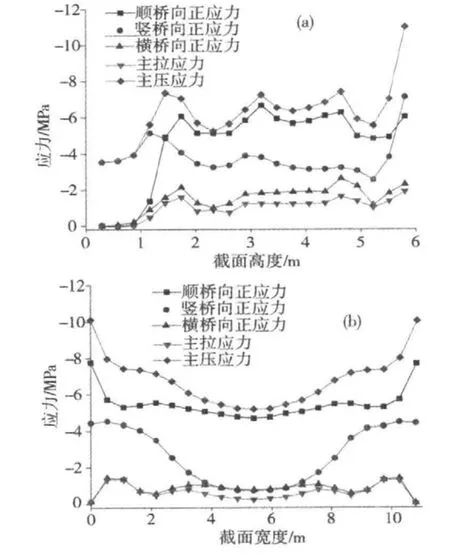
图11 C截面应力分布Fig．11 Stress distribution of section C

图12 D截面应力分布Fig．12 Stress distribution of section D

4 结论

(1)大桥所采用塔梁墩固结区构造总体上受力比较合理，应力分布较均匀，绝大部分区域的应力均能满足规范要求。

(2)主梁底板区域上下缘存在较大的拉应力，应适当加强该区域钢筋配置或增加梁体高度。

(3)固结段截面突变处，局部应力集中现象明显，建议塔柱外边缘、塔梁相交处以及固结段内部孔洞处适当设置圆倒角，尽量圆滑过渡。

(4)最大应力点附近区域应力衰减很快，应力集中仅发生在局部区域，影响范围较小。

(5)固结区压应力主要是由于主梁和桥塔的轴力引起，孔洞处应力有突变，截面应力分布呈现一定的规律性，可以用于指导结构合理配筋。

本文分析计算结果已直接应用于指导该大桥的设计，具有较高的实用价值，同时可供同类型桥梁的设计提供参考。

［1］EI Ouni M H，Ben Kahla N，Preumont A．Numerical and experimental dynamic analysis and control of a cable stayed bridge under parametric excitation［J］．Engineering Structures，2012(45):244 －256．

［2］上官萍，房贞政，卓卫东．塔梁墩固结斜拉桥结构受力分析［J］．福州大学学报:自然科学版，1999，27(3):19－22．SHANGUAN Ping，FANG Zhengzhen，ZHUO Weidong．Analysis of structural performance of cable－stayed bridge consolidated with tower，grider and pier［J］．Journal of Fuzhou University:Natural Science，1999，27(3):19 －22．

［3］卓卫东，房贞政，林清．塔梁墩固结体系斜拉桥固结节点受力分析［J］．福州大学学报:自然科学版，1999，27(4):81－85．ZHUO Weidong，FANG Zhengzhen，LIN Qing．Spatial stress analysis of fixed pier－tower－beam joint of cablestayed bridges［J］．Journal of Fuzhou University:Natural Science，1999，27(4):81 －85．

［4］彭桂瀚．斜拉桥塔梁墩固结区受力分析［J］．江南大学学报:自然科学版，2011，10(6):697 －702．PENG Guihan．Research on local behavior of pier－ tower－ girder fixed region of cable － stayed bridge［J］．Journal of Jiangnan University:Natural Science，2011，10(6):697－702．

［5］虞庐松，朱东生．部分斜拉桥塔梁墩固结点局部应力分析［J］．桥梁建设，2008(1):54－57．YU Lusong，ZHU Dongsheng．Local stress analysis of rigid fixity joint of pylon，girder and pier of an extradosed bridge［J］．Bridge Construction，2008(1):54 －57．

［6］陈启飞，李爱群，赵大亮，等．预应力混凝土斜拉桥主梁局部应力子模型分析及试验［J］．东南大学学报:自然科学版，2007，37(2):287 －290．CHEN Qifei，LI Aiqun，ZHAO Daliang，et al．Experiment and submodeling analysis on local stress in main girder of prestressed concrete cable － stayed bridge［J］Journal of Southeast University:Natural Science，2007，37(2):287－290．

［7］徐伟，李智，张肖宁．子模型法在大跨径斜拉桥桥面结构分析中的应用［J］．土木工程学报，2004，37(6):30－34．XU Wei，LI Zhi，ZHANG Xiaoning．Application of submodeling method for analysis for deck structure of diagonal cable － stayed bridge with long span［J］．China Civil Engineering Journal，2004，37(6):30 －34．

［8］周威，郑文忠．预应力等效荷载计算的通用方法及其简化［J］．哈尔滨工业大学学报，2005，37(1):49 －52．ZHOU Wei，ZHENG Wenzhong．Unified method and simplification for calculating prestressing equivalent load［J］．Journal of harbin institute of technology，2005，37(1):49－52．

［9］闫斌，戴公连．高速铁路斜拉桥上无缝线路纵向力研究［J］．铁道学报，2012，34(3):83 －87．YAN Bin，DAI Gonglian．CWR longitudinal force of cable－stayed bridge on high － speed railway［J］．Journal of the China Railway Society，2012，34(3):83 －87．

［10］刘文硕，戴公连，胡楠．高速铁路中小跨径连续梁的设计［J］．铁道科学与工程学报，2010，7(2):45 －51．LIU Wenshuo，DAI Gonglian，HU Nan．Small and medium continuous beams in high－speed railway of China［J］．Journal of Railway Science and Engineering，2010，7(2):45－51．

［11］刘雄，钟新谷，沈明燕．基于ANSYS对斜拉桥结构状况评估的有限元修正模型［J］．铁道科学与工程学报，2010，7(3):25 －30．LIU Xiong，ZHONG Xingu，SHEN Mingyan．Initial FE model research based on ANSYS software in built cable－ stayed bridge［J］．Journal of Railway Science and Engineering，2010，7(3):25 －30．