夹层橡胶垫基础隔震框架结构非线性时程分析*
蔡勇,刘光亮,陆铁坚
(中南大学土木工程学院,湖南长沙410075)
长期以来,世界各国普遍采用的结构抗震方法,是利用结构的强度和结构构件的塑性变形能力抵抗外来的地震作用。实践证明,这种方法对减轻地震灾害起到了积极作用,但在安全性与技术经济方面有着明显不足。随着科学技术的不断发展,对地震认识的不断深入,一种新的隔震设计方法“基础隔震技术”应运而生。基础隔震是在上部结构与基础之间设置侧向刚度较小的隔震层,其侧向刚度一般为上部结构刚度的1/50~1/150[1],通过隔震层位移耗能,减小结构的地震反应,从而可以减轻结构在地震中的破坏程度[2]。
1 隔震结构的动力时程分析方法
由于基础隔震技术在我国尚处于推广应用阶段[3],积累的工程经验还比较有限,因而有必要对基础隔震结构进行非线性时程分析。
1.1 基本假定
假定各层楼板为无限刚性,上部结构考虑线性地震反应,对隔震层考虑非线性地震反应。上部结构采用平动2个方向自由度,隔震层对每一个隔震器分别加以考虑,分别考虑平动两个方向自由度,通过总体刚度集成对结构进行整体动力分析,由于软件分析的局限性,没有考虑扭转作用的影响[4]。
1.2 动力分析方法
图1所示为基础隔震结构体系的动力分析模型,其中:m为结构底板的质量;mi为结构第i层的质量;ki为结构第i层的水平刚度;k为隔震装置(橡胶垫)的水平刚度;C为隔震装置(橡胶垫)的阻尼;xg和为地面地震位移、速度、加速度;xb和分别为结构底层与基础面之间的水平相对位移、速度和加速度;分别为上部结构第i层对结构底层与基础面i之间的水平相对位移反应、速度反应和加速度反应;i为隔震结构的层号(i=1,2,…,n);j为隔震结构的振型号(j=1,2,…,m)。
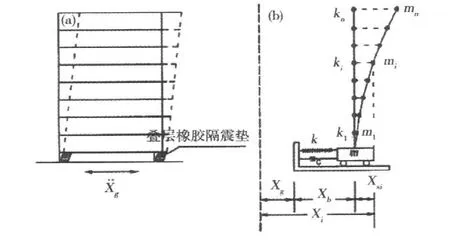
图1 多质点基础隔震结构动力分析模型Fig.1 Multi- particle model for dynamic analysis of base isolation
由图1可知,上部结构第层地震反应运动方程为:xi=xg+xb+xsi。
由达郎贝尔原理可列出隔震结构体系运动方程:
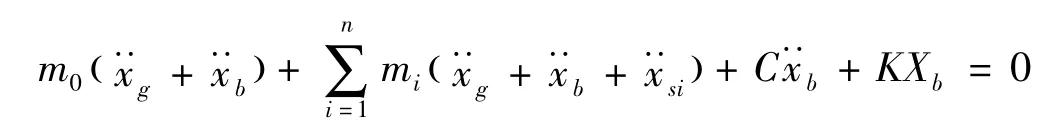
上部结构的相对运动方程为:
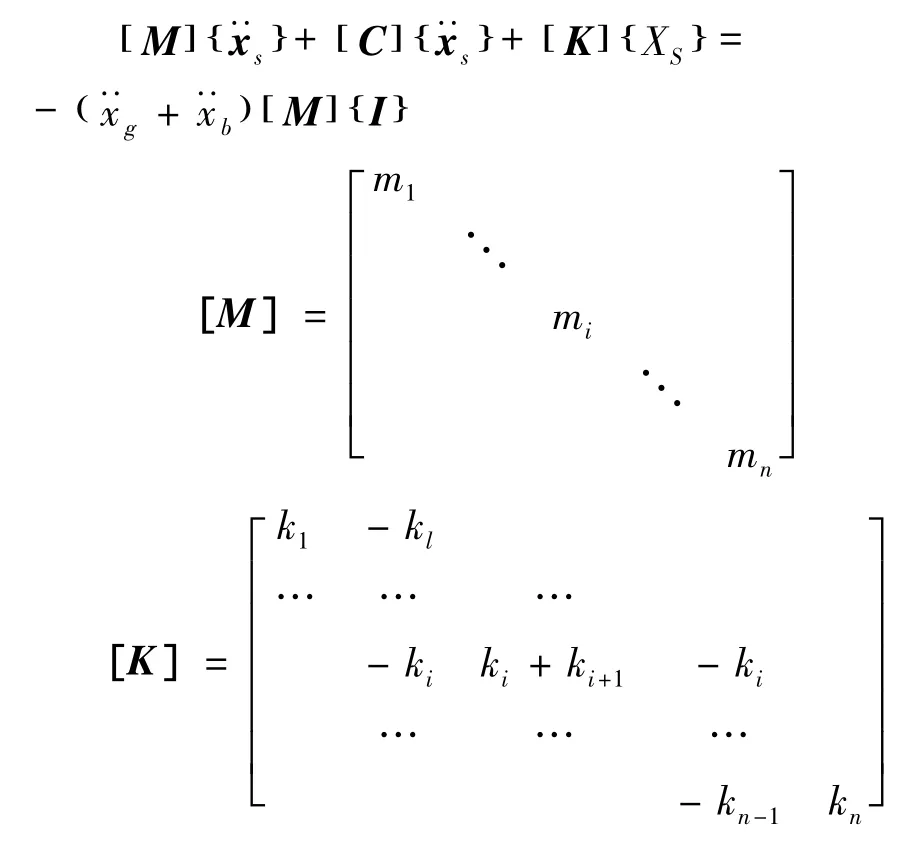
其中:[M]为质量矩阵;[K]为刚度矩阵;[C]为阻尼矩阵。
采用Rayleigh阻尼,将阻尼矩阵表示为质量矩阵和刚度矩阵的线性组合:[C]=α[M]+β[K]。常数α和β可由结构体系第i和j振型的阻尼比ζi和ζj和自振频率ωi和ωj确定,一般取i=1,j=2;
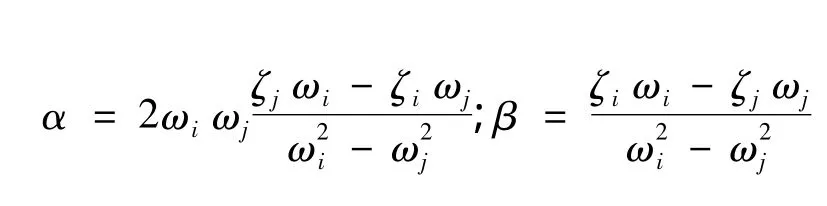
2 算例分析
2.1 工程概况
某办公楼工程为8层钢筋混凝土框架结构,平面长39.6 m,宽14.5 m,层高均为3.6 m,结构总高度28.8 m。1~3层框架柱尺寸为500 mm×500 mm,4~8层框架柱450 mm×450 mm,边跨梁(AB和CD跨)均为300 mm×500 mm,中跨(BC跨)均为250 mm×450 mm,纵向梁均为300 mm×600 mm。混凝土强度等级为板 C20,梁柱 C30,板厚120 mm,抗震设防烈度为8度,设计基本地震加速度为0.20g,钢筋混凝土框架抗震等级为二级,场地为二类,近场第1组,特征周期为0.35 s。结构平面图如图2所示。
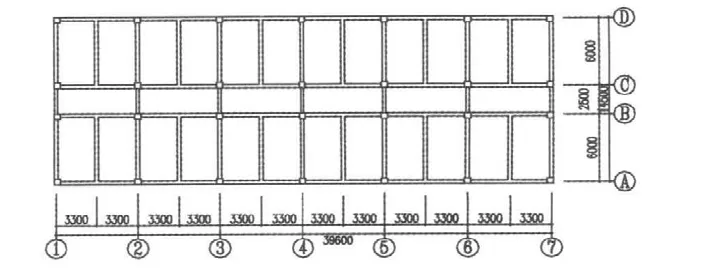
图2 结构平面布置图Fig.2 Structure of floor plan
2.2 结构模型
选用28个GZY500铅芯橡胶支座,每个框架柱下设置1个隔震支座,其形心与柱截面形心重合。铅芯橡胶隔震支座参数和性能指标见表1[5]。

表1 隔震橡胶支座力学性能Table 1 Mechanical properties of rubber bearing
2.3 有限元模型
利用有限元软件ANSYS对结构进行有限元分析,楼板选用SHELL63单元,该单元具有弯曲及薄膜特性,柱、梁选用BEAM188 3-D线性有限应变梁单元,该单元基于Timoshenko梁理论,考虑弯曲和剪切变形效应,对于隔震垫单元,在ANSYS中没有现成的隔震支座单元,本文用弹簧单元进行模拟,竖向刚度的模拟采用COMBIN14单元,两个水平方向采用 COMBIN40单元[6],依据文献[7]选用El-Centro波(NS),加速度峰值分别为0.7 m/s2和4.0 m/s2,相当于8度多遇地震和8度罕遇地震2种情况,整个时问历程20 s,时间步距0.02 s,上部结构的模态阻尼比取0.05。
2.3.1 自振特性
分别建立基础隔震结构和非隔震结构有限元模型,进行有限元分析。图3和图4所示为隔震结构的前两阶振型,表2所示为隔震结构和非隔震结构前六阶振型的自振频率和周期。
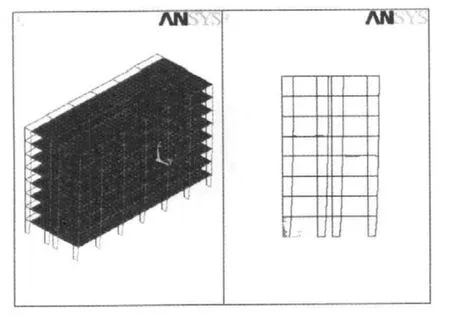
图3 隔震结构第一振型Fig.3 The first mode of isolated structure
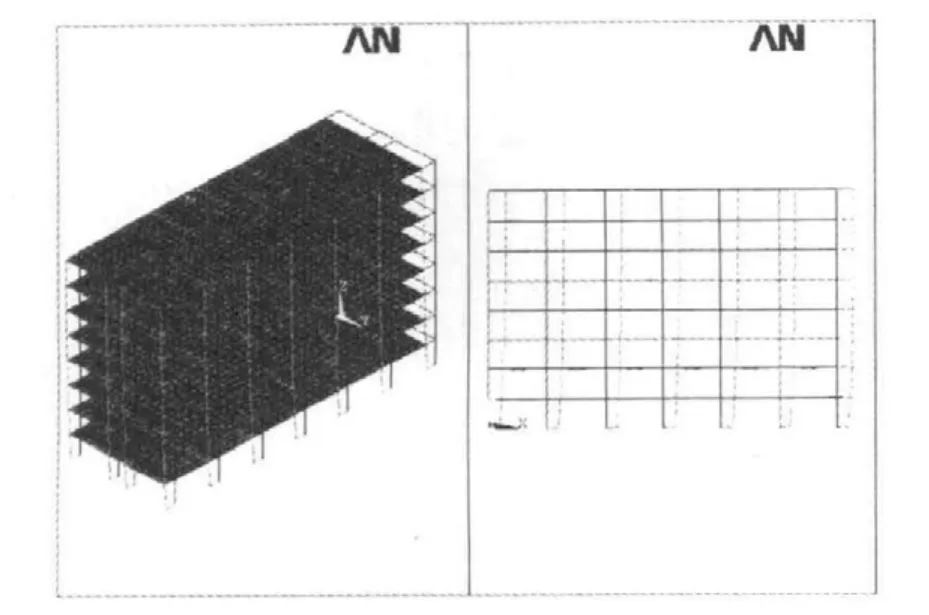
图4 隔震结构第二振型Fig.4 The second mode of isolated structure
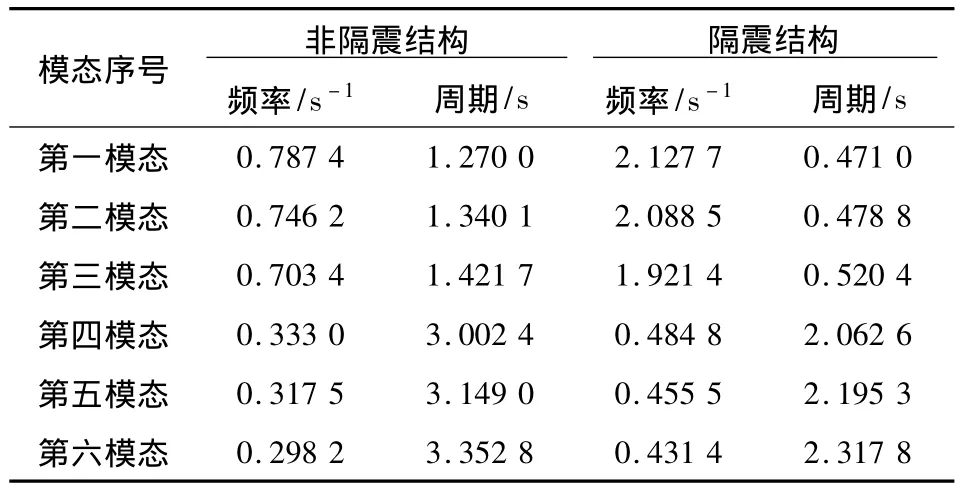
表2 隔震结构和非隔震结构模态对比表Table 2 Comparison of isolated structure and mode of non-isolated structure
从模态分析结果可以得到以下结论:
(1)隔震结构的第一自振周期为2.127 7 s,而上部结构相同的不隔震结构的自振周期为0.7 s左右,可见采用了隔震支座后,结构的自振周期大大延长,由标准地震反应谱曲线可知,结构的自振周期延长后,上部结构的加速度反应大大地减小,层间剪力也将减小;
(2)传统抗震结构的基本振型主要是下小上大的“放大型”,从隔震结构的前一,二阶振型的形状可以看出,隔震层以上结构以“整体平动”为主,同时由于高阶振型对振动的影响较小,所以,在地震中上部结构层间位移会大大地减小。
(3)隔震结构的周期远远大于不隔震结构的自振周期,从而避开了地震波的主要成分,这正是隔震结构能够减小地震作用的原因。因此,隔震结构的自振周期应该与地震波主要成分相差越大越好[8]。
2.3.2 层间剪力
从表3可以看出:
(1)最大剪力反应在隔震层底部;从底层到顶层剪力逐步减小,其中底层剪力减少的幅度很大;这充分说明隔震结构可以大幅度的降低建筑结构的底层剪力,为此隔震结构的设计可以适当的放宽限制[9]。
(2)层间剪力比最大值是计算所得实际减震系数,由规范中所规定的层间剪力和水平向减震系数的对应关系,结构减震效果相当于降低了地震烈度 1.5 度[10]。
(3)隔震结构与传统抗震结构相比,隔震结构的各层层间剪力远远小于传统抗震结构的各层层间剪力。故在相同工况下进行结构设计时,可以减少隔震结构的梁柱截面尺寸和配筋量,从而可以获得较好的经济效益。
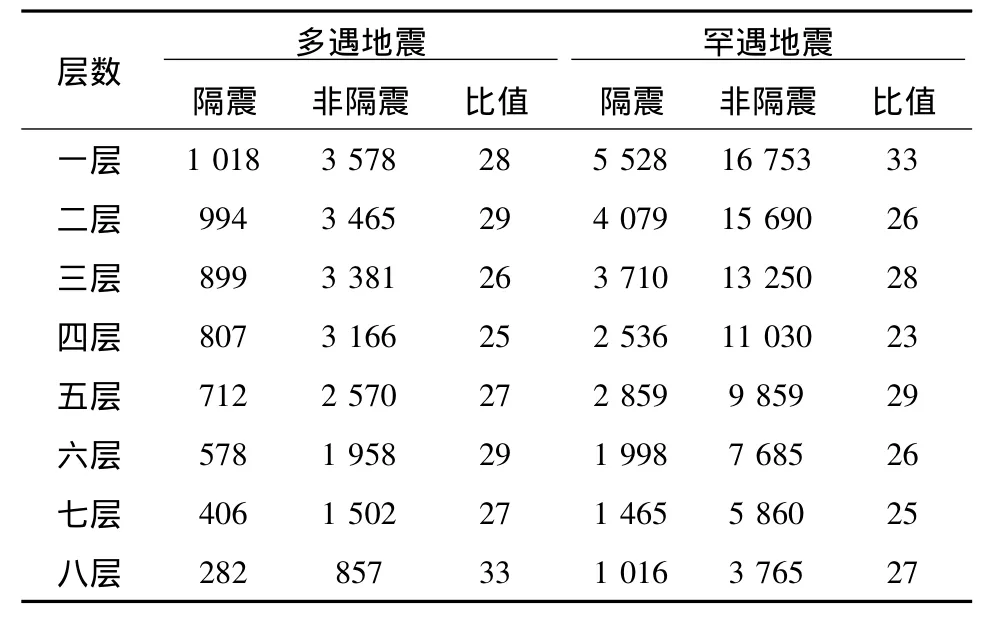
表3 剪力峰值表Table 3 Shear peak form kN
2.3.3 加速度响应
从表4可以看出:
(1)在El-Centro波多遇地震作用下,隔震结构顶层加速度峰值为0.921 m/s2,非隔震结构为3.434 m/s2,约为非隔震的1/3,大大降低了顶层的加速度,第1~8层的加速度反应规律为:加速度随着层数的提高逐渐增大,至第五层时突然减小,随后逐渐增大。
(2)隔震结构相比于非隔震结构的上部加速度,上部各层的加速度差距较小,隔震结构上部受力较为均匀,由于隔震层有滤波作用,阻隔了地震波中的某些主要频率成份向上部结构传递。因此,对结构的加速度反应进行分析,可以看出隔震效果显著。
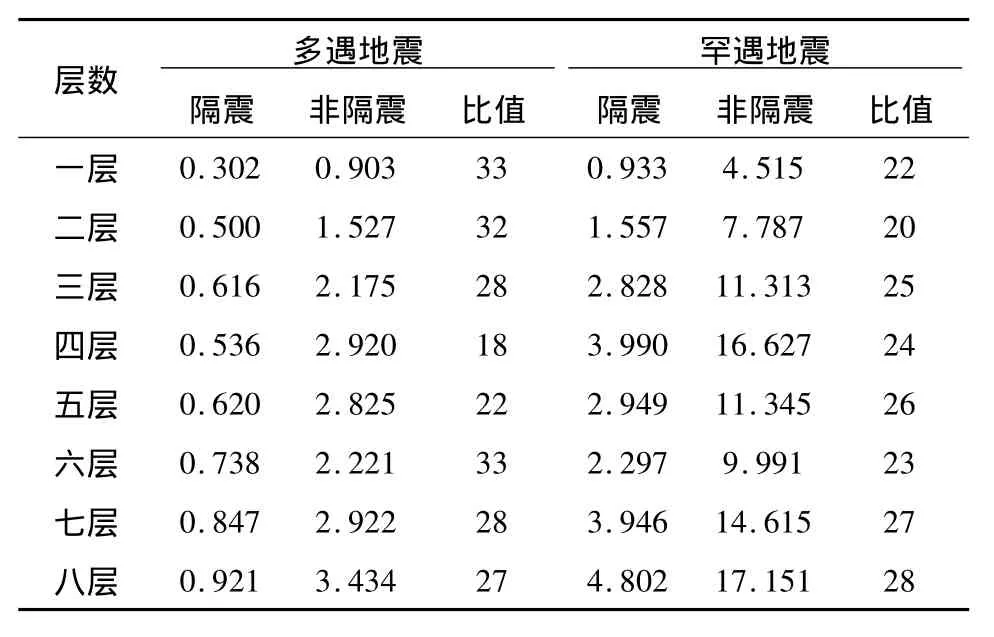
表4 加速度峰值表Table 4 Peak table acceleration m/s2
2.3.4 层间位移反应
结构各层的层间位移峰值表5所示。从表5可见:
(1)隔震结构的上部各层的绝对位移基本相同,隔震结构上部层间位移接近于零。说明上部结构在地震中是以“整体平动”为主要振动形式,上部结构基本处于弹性阶段。
(2)隔震结构多遇地震时层间位移最大值为1.35 mm,层间位移角在1/550以下,隔震结构罕遇地震时层间位移最大值为6.96 mm,层间位移角在1/50以下,不会出现因为层间位移角过大而导致结构破坏的现象。
(3)该隔震结构的隔震层位移都明显大于上部结构的层间位移,为了限制隔震层不至产生过大的位移,要求橡胶支座既要具有合适水平刚度,又要具有一定的阻尼。
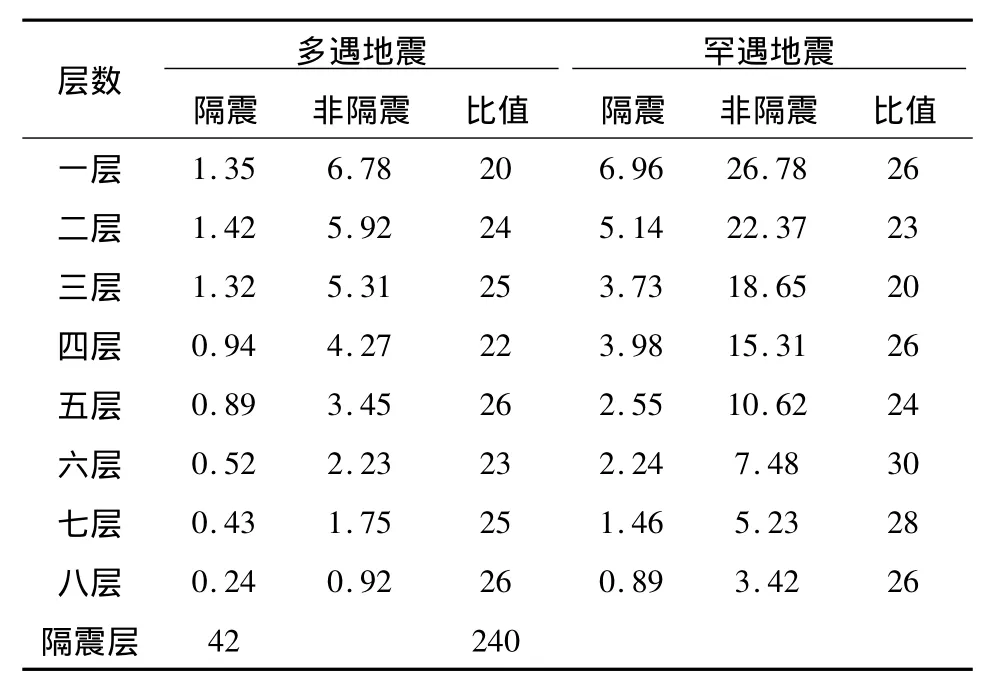
表5 层间位移峰值表Table 5 Table of interlayer displacement peak mm
3 阻尼比对隔震结构的影响
为了讨论基础隔震系统的阻尼比对框架结构加速度峰值反应的影响,固定上部结构的阻尼比ξ1=0.05,改变隔震系统的阻尼比ξ0,虽然实际上ξ0总是大于0.05,但为了完整,考虑 ξ0从0到0.5的整个范围,图5所示为顶层峰值绝对加速度反应随隔震系统阻尼比的变化关系。从图5可见:当ξ0=0.3~0.035时,其结构顶部峰值绝对加速度达到较小值;当ξ0<0.30时,其结构顶部峰值加速度随ξ0的增大而迅速减小;当ξ0>0.3时,其结构顶部峰值加速度随着ξ0的增大而增大。因此采用适当的基础隔震系统的阻尼比,可以有效降低加速度的峰值。
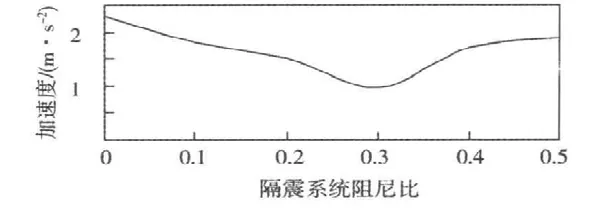
图5 隔震系统阻尼比对顶层峰值绝对加速度的影响Fig.5 Effect of isolation system damping ratio on peak absolute acceleration of the top
4 结论
(1)采用隔震技术,可以延长混凝土框架结构的自振周期,避开建筑场地的卓越周期,减少共振的发生。随着混凝土框架结构自振周期的延长,结构地震影响系数从曲线的平台段,转移到下降段,结构总地震反应得以有效降低。
(2)采用隔震装置后,结构的第一振型起决定性作用,各楼层的相对侧移很小;各楼层的最大绝对加速度明显减小,并且上部绝对加速度基本相同,从而使相对加速度减小。
(3)在地震作用下隔震结构的基底剪力、上部结构的层间剪力,比不隔震时大幅度降低,而且隔震层的水平刚度越低,隔震效果越明显,但隔震层位移随之增大,需增大隔震阻尼来减小位移。
(4)采用基础隔震技术,可减小上部框架结构的地震反应,因此钢筋混凝土框架结构的抗震要求可减低,从而降低了工程造价,并改善房屋的使用功能。
[1]刘英利,党希滨,杨平等.基础隔震结构的非线性动力分析[J].世界地震工程,2007,23(2):107-111.LIN Yingli,Dang Xibin,YANG Ping.Non - linear dynamic analysis of the base isolated structure[J].World earthquake engineering,2007,23(2):107 -111.
[2]倪国葳,张玉敏,赵亚敏.建筑结构基础隔震分析[J].地震工程与工程振动,2006,26(3):206-209.NI Guowei,ZHANG Yumin,ZHAO Yamin.Analysis of base isolation building system[J].Earthquake engineering and Earthquake engineering vibration,2006,26(3):206-209.
[3]唐家祥,刘再华.建筑结构基础隔震[M].武汉:华中理工大学出版社,1993.TANG Jiaxiang,LIU Zaihua.Base - isolated structures[M].Wuhan:Huazhong University of Technology Press,1993.
[4]邹宏德,蓝宗建,田玉基.三维多层框架隔震结构非线性时程分析[J].工业建筑,2002,(1):10-13.ZOU Hongde, LAN Zongjian, TIAN Yuji. Nonlinear timei history analysis of three-dimensional base isolated multilayer frame structure[J]. Industrial buildings,2002,(1):10 -13.
[5]魏德敏,康锦霞,韩海葳.基础隔震高层建筑地震响应的理论分析[J].地震工程与工程振动,2003,23(1):WEI Demin,KANG Jinxia,HAN Haiwei.Theoretical analysis for seismic response of a base-isolated high-rise building[J].Earthquake Engineering and Earthquake engineering vibration,2003,23(1):140 -144.
[6]陈志华,刘红波,周婷,等.APDL参数化计算与分析[M].北京:中国水利水电出版社,2009.CHEN Zhihua,Liu Hongbo,ZHOU Ting,et al.Computation and analysis of APDL Parameter[M].Beijing:China Water& Power Press,2009.
[7]王亚勇.关于设计反应谱、时程法和能量方法的探讨[J].建筑结构学报,2000,21(1):21 -28.WANG Yayong.A review of seismic response spectra,time history analysis and energy method[J].Journal of Building Structures,2000,21(1):21 -28.
[8]Wen Y K.Equivalent linearization for hysteretic systems under random excitations[J].Journal of Applied Mechnaics,ASME,1980,47(1):151 -154.
[9]周福霖.工程结构减震控制[M].北京:地震出版社,1997.ZHOU Fulin.Engineering structure damping control[M].Beijing:Earthquake press,1997.
[10]GB 50011—2001,建筑抗震设计规范[S].GB 50011—2001,Seismic Design of Buildings[S].

