基于物质灰度正态分布的CT断层图像匹配插值

吴良武 侯建华

（大连测控技术研究所，大连 116013）

引言

断层图像插值是断层图像三维重建的关键技术之一，也是一个研究得比较多的问题。一般情况下，从CT/MRI等扫描设备获得的断层图像，其层间距大于层内像素间距。数据间的这种各向异性，将会影响医学图像分析及辅助治疗系统中人体组织和器官的三维重建效果，也会给放射治疗剂量计算带来困难，因此有必要插值出各向同性的三维空间规则体数据［1］。

断层医学图像插值方法可分为基于灰度的插值方法、基于形状的插值方法和基于小波的插值方法。基于形状的插值结合从指定邻域中提取出来的各种特征，用来计算插值点灰度。该方法通常用于三维重建面绘制技术，通过已知断层图像的形状，直接构造出中间插值图像的轮廓，以方便显示［2］。基于小波的插值算法，通过改变边缘点对应小波系数的位置和强度，对灰度和形状同时插值，以充分模拟生理组织从一幅图像变化到另一幅图像的中间状态［3－4］。

基于灰度的常用插值方法有线性插值、样条插值和克立格（Kriging）插值等，从本质上说都是计算采样点灰度的加权平均，并且都根据插值点和采样点之间的相对距离来调整权值的大小。其中，线性插值是样条插值的特例。假定灰度在3个正交方向上都按样条曲线的趋势变化，用三元三次样条张量积的形式来估计插值点的灰度。由于样条插值预先假定了数据按某种样条曲线变化，当数据的实际变化规律与此有较大偏差时，则会产生不可忽略的错误。克立格插值基于数据的空间分布规律，进行统计意义上的最优无偏估计。灰度插值方法本质上是一种低通滤波，必然会对图像中的高频信息（如图像的边缘等）带来畸变，因此这类处理方式产生的结果图像普遍都存在边缘模糊的问题。

针对传统灰度插值方法所存在的问题，匹配插值的研究得到了人们的重视，比较典型的是Goshtasby等提出的基于对应点匹配的插值方法［5－6］。该方法对于插值图像中的每一个像素，根据插值点的位置选择一系列的对应点对，再通过计算对应点对的特征相似性，选择出最佳匹配点对，最后在最佳匹配点对间线性灰度插值。在Goshtasby方法的基础上，有人提出了一种基于物质分类的匹配插值方法［7］；首先计算各候选匹配点对为同种密度物质的概率S，设置判定匹配点对为同种密度物质的概率阈值，当候选匹配点对的S值大于该阈值时，认为点对中两像素点分布于同种密度物质，可作为匹配插值的进一步候选点对，然后再使用Goshtasby方法进行后续的匹配、插值等运算。匹配插值将使得插值结果图像的边缘变得清晰。还有一种方法是：根据待插值图像与其相邻原始图像的对应像素的相关性，先对像素点进行分类，然后再分别采用样条插值、匹配点线性插值等不同方式，对不同分类点进行插值，并对其进行错误校验［8］。

在当前所看到的文献中，当在匹配点对间计算插值点的灰度值时，无一例外地都采用了以距离倒数作为权值的线性插值方法。笔者基于医学CT断层图像中物质灰度呈正态分布的特性，提出了一种新的插值方法：先分割CT断层图像，在分割过程中去除孤立噪声点，然后筛选匹配点，使得候选匹配点对属于同种物质，为每个插值点搜索出各自的最佳匹配点对，最后在最佳匹配点对间，基于物质灰度的正态分布曲线获取插值权值，用来计算插值点灰度值。

1 CT断层图像分割

CT值表示对X光的吸收程度。当一个像素处于两种物质的交界处，即存在部分体积效应时，由于CT扫描设备分辨率有限，使得该像素的灰度值将位于两种物质的交叉处，如图1所示。采用阈值分割法，CT切片灰度值由低到高，可分割为空气、脂肪与软组织、骨骼3种物质，其中交叉处的像素属于混合物质。为解决部分体积效应的分割问题，吴良武等提出了一种基于邻域的骨骼确定分割算法［9］。

图1 CT切片灰度分布Fig.1 Intensity distribution of CT slices

对于单个像素点，如果在切片内，其8-邻接像素都为其他物质，而且在三维空间中，其6-邻接像素也都为其他物质，该像素将被认为是孤立的噪声点，被标定为邻域中权值最大的其他物质。在切片内，像素被看成小的正方形，8-邻接表示像素间边相连或者角相连。在三维空间中，像素被看成为体素，即小的立方体或长方体，6-邻接表示两体素间面相连。

CT图像分割后，根据文献［5，7］的方法，设定匹配窗口宽度，在匹配窗口中选取属于同种物质的候选匹配点对，分别以匹配点间灰度值的相似度、两点为中心区域的灰度变化的相似度及两点水平坐标接近程度等信息为权值，从候选匹配点对中为每个插值点搜索出各自的最佳匹配点对。

2 基于物质灰度呈正态分布特性的插值方法

把连续CT断层切片的灰度值看作随机量，直方图可以看作其概率密度函数（PDF）的估计p（z）［10］。取一组连续50层的人体头部 CT切片，图2是该组切片的脂肪和软组织灰度直方图、骨骼灰度直方图，可以看出直方图的形状都相似于正态分布曲线。笔者对另外3组医学CT断层切片也分别绘制了脂肪和软组织灰度直方图、骨骼灰度直方图，发现它们的形状也都与正态分布曲线相似。

图2 灰度直方图。（a）脂肪和软组织；（b）骨骼Fig.2 Intensity histogram.（a）Fat and soft tissues；（b）Bones

式中，μ和σ2分别表示均值和方差。

一般来说，如果一个像素全部由同种物质组成，则它的CT值应接近于某 CT0值。交叉像素由于部分体积效应，其CT值将很难稳定在 CT0值附近，使得CT断层切片中同种物质的灰度分布可能呈现出正态分布的特性。人体头部存在大块的脂肪和软组织，其交叉像素所占比例小，方差σ2值小，分布图看起来尖锐；人体头部骨骼由多个小块组成，交叉像素所占比例大，方差σ2值大，分布图看起来平坦。图2所示的灰度直方图正符合这样的解释。

基于上述分析，可认为在医学CT断层切片中，物质灰度呈正态分布特性。

灰度直方图拟合为正态分布曲线，能够去除细节，给出其光顺分布趋势。例如，拟合后，图2（b）中明显的曲线细节将会被光顺。图3显示了另一组脂肪和软组织的灰度直方图，CT扫描设备间隔取值，拟合曲线能去除取值间隔，给出光顺分布曲线。使用共轭梯度爬山法，将能使拟合的均分误差降至最小［10］。

引入约束条件“匹配点对间灰度值的概率分布与该物质的灰度正态分布一致”，由该物质的灰度正态分布定义为［11］正态分布曲线来获取计算插值点的权值，利用这种方法计算出的插值点灰度值将符合该物质的正态分布特性。图4是根据图2（b）绘制的骨骼灰度积分分布曲线，由此容易得到用于计算新插值点灰度值的权值［11］。

图3 另一组脂肪和软组织的灰度直方图Fig.3 Another intensity histogram of fat and soft tissues

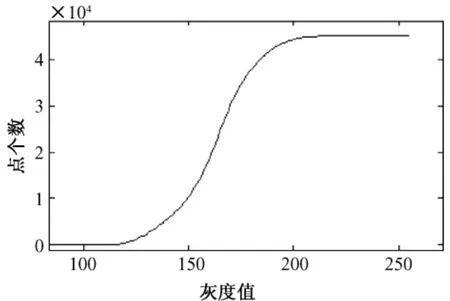
图4 骨骼灰度积分分布Fig.4 Intensity in tegraldistribution of bones

传统的同种物质匹配点对间以距离倒数作为权值的线性插值［5，7］，实际上隐含了这样的假设条件：在匹配点对的连线上，灰度值呈线性规律变化。线性变化的概率密度在统计学中是均匀分布的，其积分分布曲线为直线［11］。均匀分布与物质灰度呈正态分布特性是相矛盾的。如果匹配点对的灰度值相差不大，积分分布曲线在小区段间将可近似为直线。例如，它们都位于正态分布的顶部，或者都位于远离正态分布顶部的同一侧，那么这两点间可近似为均匀分布，此时使用线性插值与使用正态分布插值所得的结果基本没有区别。不失一般性，假设匹配点对的灰度值相差较大，一个位于正态分布顶部，另一个位于远离顶部的一侧（如图5所示），此时计算出来的结果u和v将存在较大的差异。

3 测试

图5 插值点值计算Fig.5 Calculating the value of the interpolating pixel

以上节提及的那组50层连续人体头部CT切片作为测试用例。该组50层切片是从头顶部位向下顺序生成，切片间距为1.84 mm，图6列出了其中的前10幅连续切片，图中采用字母表示切片序号，测试结论将主要针对这10幅连续切片给出。去除切片中与人体头部无关的背景固定物，定义灰度值大于135的像素为确定骨骼，灰度值介于65～115之间的像素为确定脂肪与软组织，灰度值小于45的像素为确定空气，灰度值介于115～135之间及介于45～65之间的像素为不确定像素。

每次测试选取3幅连续切片，从前、后切片中插值新切片，然后与中间原始切片做比对，计算插值与真实值间的偏差。

图6 连续CT头部切片。（a）～（j）为从头顶部位开始的切片序列Fig.6 Continuous CT slices of the head.（a）～（j）The sequences of slices beginning at the top of the head

CT切片分割后，按照文献［5，7］的方法，先为每一插值点搜索属于同种物质的最优匹配点对，然后在最优匹配点对间，分别使用线性插值与正态分布插值，计算插值点的灰度值。只讨论两种方法插值结果灰度值差大于2的插值点，对它们作标记，采用标记点的均偏差对插值结果的优劣进行评价。以N表示每次测试的标记点总数，v表示计算出的标记点插值，v0表示标记点真实值，每次测试的均偏差e定义为

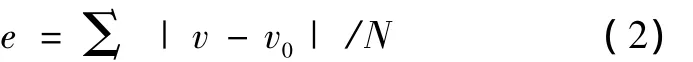
测试分两组进行。第1组测试在确定像素间进行，也就是说，候选匹配点对都为同种物质的确定像素。第2组测试规定只要有一个像素为确定像素，另一个像素如果为该物质的不确定像素，则它们也可以作为候选匹配点对。这样，第2组测试中将包含较多的匹配点对，一个为确定像素，另一个为不确定像素。

4 结果

测试结果如表1和图7所示。表1列出了中间比对切片序号为（b）～（h）的7次测量数值结果。EN1列列出了第1组测试使用正态分布插值的标记点均偏差值，EL1列列出了第1组测试使用线性插值的标记点均偏差值；EN2列列出了第2组测试使用正态分布插值的标记点均偏差值，EL2列列出了第2组测试使用线性插值的标记点均偏差值。

将表1的测试结果绘制于图7中。图7的横坐标表示每次测试的中间比对切片序号，其中的横坐标2对应切片（b），横坐标3对应切片（c），依此类推，纵坐标表示每次测试标记点的均偏差 e。50幅连续切片共进行48次测试，图7列出了其中的前20次测试结果，绘制出了第1组线性插值和正态分布插值的均偏差曲线，以及第2组线性插值和正态分布插值的均偏差曲线。

表1 测试结果Tab.1 Experimental results

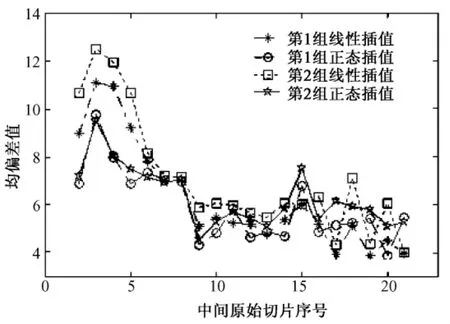
图7 均偏差比较Fig.7 Comparison of average errors

先比较线性插值与正态分布插值的测试结果。从图7可以看出，在前4次测试中，用正态分布插值方法得到的两组均偏差明显都比用线性插值方法的小。表1的数据也说明了这一点：在前4次测试中，第1组正态分布插值得到的均偏差比线性插值得到的均偏差平均减小了21.5％，第2组正态分布得到的均偏差比线性插值得到的均偏差平均更是减小了29.55％。不过，后续的测试结果则很难看出其中的明显差别。图7未列出的后28次测试结果也很难看出明显差别。

查看图6，从（a）～（f）的切片位于头部的顶部，用于测试的前、后两幅切片对应像素的灰度值差别比较大，使得前4次测试所搜索到的最佳匹配点对中，存在灰度值差大的匹配点对较多。例如，在使用切片（a）和切片（c）插值的测试中，可以观察到切片（c）中很多骨骼像素在切片（a）中的对应匹配点的灰度值都比较小，导致最佳匹配点间差值大的插值点增多，这种现象直到中间切片序号为（e）的测试中都有存在。但在后续的测试中，前、后切片相似度比较高，如切片（f）和切片（h）之间的相似性要高很多，导致搜索到的最佳匹配点间差值并没有那么明显。在前4次测试中，因为正态分布插值方法改进了线性插值方法处理匹配点间差值大的情况，使得标记点的均偏差变小，后续测试均偏差没有明显变化，是因为后面的前、后切片相似度比较高，导致搜索到的最佳匹配点间差值大的插值点少。此时，如上节所述，两种插值方法得到的结果没有大的差别。

再比较第1组与第2组的测试结果。从图7可以看出，在前4次测试中，线性插值在第2组测试中得到的标记点均偏差明显比第1组测试增大，从表1可计算出平均增大了14.43％，正态分布插值方法的标记点均偏差在两组测试中则基本保持不变。这说明，随着匹配点间差值大的插值点增多，线性插值方法的标记点均偏差也在变大，而正态分布插值方法的标记点均偏差基本保持不变，表明正态分布插值方法与实际情况更相符。

上述两种测试分析结果都说明，基于正态分布的插值方法改进了当前最佳匹配点对间普遍采用的线性插值方法，正确修正了其中的匹配点间差值大的插值点的插值，从而整体上提高了插值效果。

5 结论

本研究基于CT断层切片同种物质灰度呈正态分布的特性，引入了约束条件“匹配点对间灰度值的概率分布与该物质的灰度正态分布一致”，在最佳匹配点对间，基于物质的灰度正态分布获取权值，计算插值点的灰度值。测试结果表明，这种方法改进了当前匹配点对间普遍采用的线性插值，正确修正了其中的匹配点间差值大的插值点的插值，从而整体上提高了插值效果。对于其他类型的医学断层切片匹配插值，该插值方法应该也具有一定的参考应用价值。

［1］陈武凡，秦安，江少峰，等.医学图像分析的现状与展望［J］.中国生物医学工程学报，2008，27（2）：175－181.

［2］GreveraGJ， Udupa JK. Shape － based interpolation of multidimensional gray-level images［J］.IEEE Trans on Medical Imaging，1996，15（6）：881－892.

［3］黄海赟，戚飞虎，陈剑，等.基于小波的医学图像插值［J］.自动化学报，2002，28（5）：722－728.

［4］胡俊峰，唐鹤云，钱建生.基于小波变换医学图像融合算法的对比分析［J］.中国生物医学工程学报，2011，30（2）：196－205.

［5］Goshtasby A，Turner DA.Matching of tomographic slices for interpolation［J］. IEEE Transactions on Medical Imaging，1992，11（4）：507－516.

［6］缪晓和，邓元木，黄斐增，等.基于对应点匹配的断层图象三维插值方法［J］.中国医学物理学杂志，2000，17（1）：14－16.

［7］张勇，欧宗瑛，秦绪佳，等.基于物质分类的三维空间断层图像匹配插值［J］.计算机辅助设计与图形学学报，2002，14（7）：559－663.

［8］田沄，齐敏，卫旭芳，等.基于像素分类的医学图像层间插值［J］.中国图象图形学报，2008，13（9）：1655－1660.

［9］吴良武，侯建华，张勇，等.用邻域运算从 CT图像中分割骨骼［J］.中国生物医学工程学报，2003，22（3）：199－202.

［10］冈萨雷斯，著.阮秋琦，译.数字图像处理（第2版）［M］.北京，电子工业出版社，2005，489－493.

［11］马洪宽，张华隆，主编.概率论与数理统计［M］.上海：上海交通大学出版社，2005.