信噪比对不同EIT图像重建算法的影响研究及评价

邓 娟 陈素华 沙 洪 赵 舒 任超世*

1（南昌大学信息工程学院电子信息工程系，南昌 330031）

2（中国医学科学院＆北京协和医学院生物医学工程研究所，天津 300192）

引言

电阻抗断层成像以人体组织、器官的阻抗分布或阻抗变化为依据，通过配置于人体体表的电极系统，提取与人体生理、病理状态相关的组织或器官的电特性信息，给出反映组织、器官功能状态及其变化规律的功能性图像结果。国外的EIT研究一直很活跃，一些小组已由实验室研究向临床应用研究过渡［1－3］。国内20世纪90年代末陆续进行EIT系统研究，已建立多个EIT实验装置和研究平台，并在乳腺肿瘤检测和脑、腹部渗血监护和肺功能测量等方面向临床应用研究发展［4－7］。我国的阻抗成像研究起步较晚，与国外的差距依然存在，但现已具备相当的基础，从方法学研究向应用基础和临床应用研究过渡的时机已经成熟［8］。

EIT系统主要包括数据检测系统和图像重构算法两个部分，两者相互依赖，互相补充。以往的EIT方法学研究旨在探索EIT成像原理，希望影响因素最少，通常假设EIT检测系统是理想的，具有最高的检测灵敏度和最佳的信噪比。然而，实用化EIT测量与理想仿真时的条件差别很大。比如，由于检测系统有限的测量精度和动态范围，测量数据精度和噪声的关系十分重要；对于不同位置目标的成像，检测系统信噪比对不同激励-测量模式和图像重建算法应用效果的发挥和影响也有差异。

Rafiei-Naeini和McCann认为，提高EIT检测系统的信噪比，可以有效改善系统的检测灵敏度和空间分辨率，而其中电流激励子系统信噪比的提高对整个系统信噪比的提高将有很大贡献。他们采用模拟和数字电子技术，设计了一种信噪比为80 dB低噪声的电流激励源子系统。该系统输出阻抗达到10 MΩ，激励频率在10 kHz～4 MHz之间变化时产生的漂移较小［9］。Alder等认为，一个优化的EIT检测系统应对场域电导率变化有较好的分辨率，而这个分辨率可以表示为EIT系统的电极数和激励电流幅度、兴趣区电导率变化量、目标位置和大小、激励测量模式和测量噪声的函数。该分辨率正比于与阻抗变化幅度，反比于噪声幅度［10］。鉴于EIT对测量边界的噪声十分敏感，Franciane通过在仿真数据中加入高斯白噪声，研究了相邻激励和相对激励的抗噪性能，发现相邻激励无法较好地解决含噪信号图像重建的问题，而相对激励则能较好地重建且成像误差较小［11］。Wang等提出，在小电压信号测量上，采取比大信号花费更长的采集时间来进行噪声补偿的处理方法［12］。罗辞勇等提出，采用一种交叉测量协议，不单纯采用相邻测量模式，通过增大测量电极间隔，获取测量数据中较大的电压进行图像重建，并从提高EIT检测信号的抗噪性能、改善灵敏度和降低病态性等方面表明了交叉测量模式的实用化效果［13］。在算法方面，Kao等提出Tikhonov和Noser类组合正则化算法，降低噪声影响的同时准确定位目标［14］。

鉴于国内外EIT研究正从方法学研究向应用基础和临床应用研究过渡，为针对具体应用目标构建EIT检测系统，以及评价实用化EIT系统的性能，在不同位置单目标和多目标EIT成像中，探索不同信噪比的实用化EIT系统对不同的重建算法的影响以及相应图像重建效果的定量评价十分必要。

1 方法

笔者通过仿真的方法模拟不同信噪比的实用化EIT检测系统和不同位置的成像目标，比较不同算法的成像结果和性能，因此构建了基于Matlab的EIT-GUI软件研究平台。应用这一研究平台，可进行自适应剖分，EIT问题正向计算和多种算法的图像重建。图像重建过程中，剖分层数、电极数目和激励-测量模式可选。假设EIT图像重建的是圆形场域，应用平台进行7层三角剖分，并在场域表面安置16电极，如图1所示。其中，场域表面编号1～16位置处用于放置电极，图1中表示采用电极对（1，2）进行相邻激励，采用电极对（3，4）进行相邻电压测量，这里假设电极为点电极。

图1 EIT场域电极位置及激励－测量方式Fig.1 The electrodes position and excitementmeasurement pattern of EIT field

1.1 不同信噪比实用化EIT系统的模拟

针对16电极EIT系统，通过仿真获取EIT场域边界电压作为理想EIT系统的采集信号。由于测量数据众多，考虑所有检测数据的影响，将所有数据检测通道视为一个整体，对理想系统所有通道采集的数据整体添加高斯白噪声，模拟一定信噪比的EIT检测系统的测量电压。SNR定义为

式中，i=1，2，…，n，n表示一次图像重建所用的测量数据。voi是理想仿真条件下获得的边界电压信号，vfi是仿真条件含有高斯分布噪声的仿真检测信号。模拟SNR分别为40、60、80 dB的实用化EIT系统。

1.2 EIT图像重建算法

采用5种图像重建算法，分别为反投影算法（lines back projection，LBP）、基于牛顿－拉夫逊（Newton-Raphson）算法的Tikhonov正则化算法（NR Tikhonov）和Tikhonov-Noser组合正则化算法（NR Tikhonov-Noser），以及Landweber二阶迭代算法（Landweber）和Newton-Raphson算法。

LBP是基于反投影理论的算法。Landweber二阶迭代法基于灵敏度系数理论，是最速下降法的一种变形，以迭代的方法逼近灵敏度系数矩阵的逆阵［15］。牛顿-拉夫逊算法是无约束极小化的一种迭代算法，它使用二次函数近似代替目标函数［16］。为解决EIT图像重建的不适定性问题，可以进行正则化。Tikhonov正则化算法采用单位矩阵，作为正则化矩阵，该方法可以很好地去除噪声，但是由于给系数矩阵加入了单位矩阵容易产生伪像［17］。Cheney等采用对角矩阵进行正则化，称为NOSER类正则化，该方法可提供正确的目标位置，但重建时噪声过大［18］。Kao等人于2006年提出Tikhonov和Noser类组合正则化算法，组合正则化方程为

g=（STS+εT×I+εN×diag（STS））－1STz（2）式中，εN代表Noser类正则化参数，而εT代表Tikhonov正则化参数；S代表灵敏度系数矩阵，而I代表单位矩阵；diag（STS）表示由正定阵STS生成的对角矩阵。

1.3 EIT图像质量评价方法

研究表明，同一算法用于不同的成像目标（大小或位置不同），不同算法用于同一成像目标，其重建结果在图像质量、信息量上有较大差异［19］。医学图像质量的评价一般分为主观评价方法和客观评价方法。主观评价方法常根据事先规定的评价尺度或自己的经验，按视觉效果对待测图像质量进行判断，易受到观察者的知识背景、观测目的和环境等影响，难以用数学模型表达，因此无法广泛推广应用。客观质量评价方法依据数学模型给出的量化指标衡量医学图像质量，弥补了主观评价方法的不足，已经成为医学图像质量评价研究的重点［20］。建立客观、定量的EIT图像评价方法，也是目前EIT研究和应用中急需解决的问题之一。EIT通过有限元剖分方法求解，各剖分单元的电导率仍然是通过数值填充来进行显示的。对于这种填充的图像，引入图像重建误差函数ER定量评价图像重建误差，用图像的结构相似度函数SSIM，定量比较和评价重建图像对目标分辨和定位的能力［21－22］。

1.3.1 图像重建均方误差ER

定义EIT图像重建误差函数ER为式中，M为有限元剖分的总单元数，GX（p）为成像模型各单元电导率，GY（p）为重建图像各单元电导率，ER表示图像重建前后每个单元的重建图像电导率和模型电导率的误差。

通过ER可获得重建图像和成像模型之间的差别，可灵敏地反映重建图像的质量。ER值越小，表示成像结果与模型的差别越小，图像重建质量越高。

1.3.2 结构相似度函数SSIM

定义图像X，Y的结构相似度为［23］

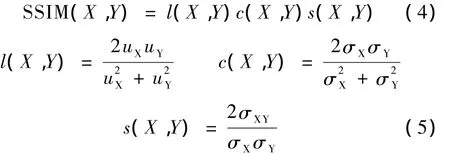
式中，uX，uY，σXY分别表示已有电导率分布的模型图像X和重建的电导率分布图像Y的均值、方差和协方差，图像的均值、方差（标准差）可以看作是对图像亮度、对比度的粗略估计，而协方差则是重建图像相对于成像模型的非线性改变。因此，l（X，Y），c（X，Y），s（X，Y）可以分别看作亮度比较、对比度比较和图像结构比较［23］。在图像中，这3项是独立的，单纯的亮度、对比度改变并不会影响第3项。SSIM为

SSIM（X，Y）∈［0，1］，当 EIT重建图像与检测模型图像完全相同时，SSIM（X，Y）=1，即结构相似度SSIM的值越接近于1，成像质量越好。

2 不同信噪比条件下不同算法的仿真成像

仿真实验中，采用16电极EIT系统，激励电流为1mA，均匀场电导率设置为0.1 Ω－1m－1，成像目标电导率设置为0.01 Ω－1m－1。由于场域中不同位置的成像目标成像结果的差异较大，设放置在成像场域中不同位置的单个目标模型为A、B、C，两个目标模型为D和4个目标模型为E。图2～图4分别为在40、60、和80 dB信噪比EIT系统条件下，采用不同算法对不同目标的仿真成像结果。表1～表3为采用图像重建误差函数ER和结构相似度函数SSIM对图2～图4的定量评价结果。

图2 40 dB EIT系统下不同算法的图像重建结果Fig.2 The reconstruction results of different algorithms when the SNR is 40dB

表1 40 dB EIT系统下用不同算法重建图像的定量评价Tab.1 The quantitative evaluation of reconstruction image of different algorithms when the SNR is 40 dB

图2的成像结果表明，在信噪比为40 dB EIT测量系统条件下，对于场域中心的目标A，仅LBP和NR Tikhonov-Noser可以成像。对所设其他4个目标模型成像，5种算法成像效果的差异较大。采用ER和SSIM定量评价的结果表明，单目标成像中，当目标由场域中心向测量浅表移动（依次是目标A、B、C），5种算法的SSIM都增大，这提示算法对目标的定位能力增大。当目标位置都靠近浅表但个数增加时（依次为单目标C、双目标D和4个目标E），5种算法的ER都呈现出增大的趋势，这表明图像重建的误差随成像目标个数的增加而增大。

图3 60 dB EIT系统下不同算法的图像重建结果Fig.3 The reconstruction results of different algorithms when the SNR is 60 dB

表2 60 dB EIT系统下不同算法重建图像的定量评价Tab.2 The quantitative evaluation of reconstruction image of different algorithms when the SNR is 60 dB

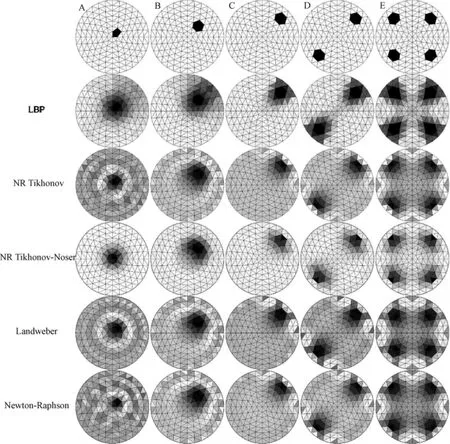
图4 80 dB EIT系统下不同算法的图像重建Fig.4 The reconstruction results of different algorithms when the SNR is 80 dB

通过定量评价结果对5种成像算法的性能进行分析发现，无论目标位于何处，NR Tikhonov-Noser算法都可以有效成像，且成像结果都具有最大的SSIM，除在对目标B的成像中其ER略大于LBP外，还具有最小的ER，其成像效果最好。LBP算法的ER仅次于NR Tikhonov-Noser算法，提示其成像误差较小；但同时其SSIM值也是最小，表明其重建图像对目标的分辨和定位能力较差，虽然能识别目标，但往往有干扰目标识别的成像噪声存在。尽管如此，LBP能对场域中心的目标A成像，这一优势也是除NR Tikhonov-Noser算法外其他3种算法所不能及的。NR Tikhonov、Landweber和Newton-Raphson算法的成像效果接近，其ER和SSIM值互相交叉，它们的成像效果明显不如NR Tikhonov-Noser正则化算法的成像效果。对于它们可成像的目标（除目标A外），其成像误差ER比LBP大，但结构相似度SSIM也大，各有可取之处。

EIT测量系统信噪比达到60 dB时，图3的结果表明仅NR Tikhonov和Landweber二阶迭代算法不能对场域中心的单目标A成像，5种算法对各个目标的成像效果相对于40 dB时也有较大改善。表3采用函数ER和SSIM定量评价，发现目标由场域中心向测量浅表移动时5种算法的SSIM都增大。当目标个数增加，5种算法的ER都呈现出增大的趋势，这与40 dB时类似。根据表3的评价结果来比较5种算法的性能，发现NR Tikhonov-Noser算法的优势仍然较为明显，对所有成像目标的图像重建结果都有最小的ER，除目标B的SSIM略小于Landweber算法外还具有最大的SSIM，成像效果是最好的，尤其是靠近浅表的目标C、D、E。NR Tikhonov、Landweber和Newton-Raphson算法的成像效果相近，成像和定量评价的结果表明，它们的成像质量相对于40 dB时改善较大，提示EIT系统信噪比的提高对这3种正则化算法成像效果的改善具有较好的作用。在40 dB信噪比测量系统下，LBP算法可对所有目标成像且其ER较小，但在60 dB下优势已不明显。

表3 80 dB EIT系统下用不同算法重建图像的定量评价Tab.3 The quantitative evaluation of reconstruction image of different algorithms when the SNR is 80dB

图4和表3的结果表明，当系统信噪比达到80 dB时，5种算法均可对设定的5个目标有效成像。其中，NR Tikhonov和Landweber算法获得了最为明显的改善，对中心目标A实现了有效成像。相对于60 dB下的图像重建，NR Tikhonov-Noser算法的重建效果略有提高，改善不大。对于同一目标的成像，相对于60 dB时LBP的ER明显减小，SSIM增大，重建效果获得了较大的改善。Newton-Raphson的图像重建也获得了更优的结果。提示具有80 dB信噪比这一参数的EIT系统足以保证本研究采用的5种算法对不同成像目标有好的成像效果。对于NR Tikhonov-Noser算法，再继续提高EIT系统的信噪比性能，通过算法来获得成像效果改善的可能性不大。

3 讨论与结论

笔者立足于实用化EIT测量与理想的仿真成像的差异，仿真研究了不同位置单个目标和多个目标的成像中信噪比对5种图像重建算法性能的影响，发现EIT系统的信噪比不足将影响成像算法的应用效果。在40、60、80 dB信噪比下，对不同算法的图像重建结果和评价结果综合分析如下：

1）无论系统信噪比是40、60还是80 dB，在单目标成像中，当目标由场域中心向测量浅表移动（依次是目标A、B、C），5种算法的仿真成像图与目标模型图的结构相似度都增大，提示算法对目标的定位能力增大；当目标位置都靠近浅表但个数增加时（依次为单目标C、双目标D和4个目标E），5种算法的ER都呈现出增大的趋势，表明图像重建的误差随成像目标个数的增加而增大。

2）在5种算法中，NR Tikhonov-Noser算法表现出较大的优势。一方面，体现在该算法可在信噪比较差的EIT系统下有效成像；另一方面，在同样的信噪比EIT系统和相同成像目标条件下，该算法的成像质量更高。究其原因，主要是算法加入了单位矩阵提高了抗噪性，加入了对角矩阵能减少单位阵带来的伪像，提高了算法对目标的分辨和定位能力，从而提高了成像质量。

3）对于场域中心的目标A，Newton-Raphson算法在40 dB信噪比时无法成像，NR Tikhonov，Landweber在40和60 dB时均不能获得有效图像。究其原因，一方面，是目标靠近场域中心，形状也不是完全的中心对称，而这些算法都采用了灵敏度系数矩阵，由灵敏度系数理论可知，场域边界灵敏度较高且电极附近灵敏场变化剧烈，而中心区域灵敏度低且变化缓慢；另一方面，NR Tikhonov-Noser算法也基于灵敏度系数矩阵，而40 dB即可对A成像，这三种算法抗噪性不及NR Tikhonov-Noser算法；再者，实验中将所有通道的测量数据视为一个整体加入高斯白噪声，也可能是导致无法成像的一个因素。事实上，由于方法和实验实际情况的差异，在研究过程中研究者们加入和定义信噪比的方法不尽相同。如罗辞勇等人在研究不同测量方法的抗噪性的过程中，就定义信噪比为最大测量电压的信噪比，他们在40 dB时即获得了对场域中心的圆形规则目标的有效成像结果［13］。这些因素和影响有待于实际EIT检测系统实验的进一步验证。

4）不同的图像重建算法和不同成像目标对成像系统的信噪比要求不一致。本仿真结果可指导实用化EIT系统的构建过程中系统信噪比指标的设计，应根据其应用对象（如检测目标位置）和拟采用的算法，避免造成信噪比不足无法有效成像，或避免过高的信噪比给硬件设计带来难度。对于NR Tikhonov-Noser算法，40 dB的信噪比即可对场域内目标成像，60 dB的信噪比足够获得场域中心处较高质量的图像。Newton-Raphson算法在60 dB信噪比的系统中时可对场域中心目标成像，而对于NR Tikhonov和Landweber算法80 dB才能实现这一目标。对于已经构建好的系统，可根据实际成像结果估计其信噪比，从而对一定的成像目标选择更适合的图像重建算法。NR Tikhonov-Noser算法可作为一般情况下的首选算法。除NR Tikhonov-Noser算法外，系统信噪比在40 dB左右或者40～60 dB时可选择LBP。低于60 dB的系统，对于场域中心目标的成像，不建议选择NR Tikhonov、Landweber和Newton-Raphson算法。在80 dB时，虽然LBP算法相对于40和60 dB时自身性能有所改善，但相对于其他算法成像效果不够理想，所以不建议选择，除此之外的其余4种算法均可选。

EIT方法学研究采用理想化的测量系统，然而实用化EIT系统的信噪比总是有限的。在EIT检测系统信噪比一定的情况下，系统往往缺乏必要的数据分辨能力，影响算法应用效果的发挥。不同的算法由于各自的原理和抗噪性能不同，在不同的信噪比条件下表现出不同的性能，得到不同的图像重建结果。在构建EIT检测系统时，信噪比指标应根据其应用目标和拟采用的算法进行设计。已经构建好一定信噪比的系统，应根据具体成像目标，选择更适合的图像重建算法。

本研究仅探索了不同的EIT检测系统信噪比对不同图像重建算法应用效果的影响。在实际情况下，除了噪声引起的误差，电极间不匹配也会引起的误差；实际电极也不是点电极，而是具有一定大小的面，电极与皮肤的接触阻抗也将引起误差；电极位置移动，也会给成像引入伪差；检测系统灵敏度的不足，也会影响到图像重建的效果，等等。这些都是EIT走向实用化的过程中必须解决的关键问题，有待于深入研究。

［1］Trokhanova OV，Okhapkin MB，Korjenevsky AV.Dualfrequency electrical impedance mammography for the diagnosis of non-malignant breast disease［J］.Physiol Meas，2008，29（6）：S331－S344.

［2］Demidenko E.An analytic solution to the homogeneous EIT problem on the 2D disk and its application to estimation of electrode contact impedances［J］.Physiol Meas，2011，32（9）：1453－1471.

［3］Chakraborti KL，Selvamurth W.Clinical application of Electrical Impedance Tomography in the Present Health Scenario of India［J］.Journal of Physics：Conference Series，2010，224（1）：69－72.

［4］徐桂芝，王明时，李有余，等.医用电阻抗成像系统的模块化设计［J］.天津大学学报，2006，39（S1）：133－137.

［5］Sha Hong，Wang Yan，Zhao Shu，et al.Integrated data collection in electrical impedance tomography［C］.//Scharfetter H，Merva R，eds.IFMBE Proceedings.Berlin：Springer，2007：348－351.

［6］史学涛，霍旭阳，尤富生，等.颅内出血电阻抗成像系统及初步动物实验［J］.航天医学与医学工程，2007，20（1）：24－27

［7］刘丹丹，乌日图，王超，等.基于医学阻抗技术的乳腺癌检测方法［J］.电子测量技术，2008，31（4）：60－64.

［8］任超世，李章勇，王妍，等.电阻抗断层成像应用基础与临床应用的一些研究进展［J］.中国生物医学工程学报，2010，29（2）：300－304.

［9］Rafiei-Naeini M，McCann H.Low-noise current excitation subsystem for medical EIT ［J］.Physiol Meas，2008，29（6S），173－184.

［10］Adler A，Gaggero P，Maimaitijiang YS.Distinguishability in EIT using a hypothesis-testing model［J］. Journal of Physics：Conference Series，2010，224（1）：56 － 59.

［11］Franciane CP，Luis PSB.Somenumerical results on the inuence of measurement strategies and load patterns in the EIT inverse problem ［J］.Journal of Physics：Conference Series，2010，224（1）：145－148.

［12］Wang W，Brown BH，Leatilard AD，et al，Noise equalisation within EIT images［J］.Physiol Meas，1995，15（S2A）：211 －216.

［13］罗辞勇，陈民铀，王平.电阻抗成像交叉测量模式的抗噪性能研究［J］.仪器仪表学报，2009，1（1）：1－6.

［14］Kao TJ，Isaacson D，Newell JC，et al.A 3D reconstruction algorithm for EIT using a handheld probe for breast cancer detection［J］.Physiol Meas，2006，27（5）：1 － 11.

［15］Yang WQ，Spink DM，York TA，et al.An image reconstruction algorithm based on Landweber iteration method for electrical capacitance tomography［J］.Meas Sci Technol，1999，10（11）：1065－1069.

［16］Yorkey TJ，Webster JG，Tompkins WJ.An improved peurtbration technique for electrical impedance imaging with some criticisms［J］.IEEE Trans Biomed Eng，1987，BME － 34（11）：898 －901.

［17］Vauhkonen M，Vadasz D，Kaejalainen PA，et al.Tikhonov regularization andpriorinform ationin electricalimpedance tomography［J］.IEEE Trans on Medical Imaging，1998，17（2）：285－293.

［18］Cheney M，Isaacson D，Newell JC，et al.NOSER：an algorithm for solving the inverse conductivity problem.International Journal of Imaging Systems and Technology［J］.1990，2（2）：66 － 75.

［19］董秀珍，秦明新，付峰，等.生物电阻抗断层成像技术的研究进展［J］.第四军医大学学报，1999，20（3）：252－255.

［20］段影影，马建华，陈武凡，等.改进的结构相似医学图像质量评价方法［J］.计算机工程与应用，2010，46（2）：145－149.

［21］吕婧华，宫伟彦，王妍，等.基于梯度误差电阻抗断层成像技术的图像评价［J］.中国组织工程研究与临床康复，Vol 12，2008（52）：10277－10280.

［22］Wang Yan， ShaHong， RenChaoshi. Optimum designof electrode structure and parameters in electricalimpedance tomography［J］.Physiol Meas，2006，27（3）：291 – 306.

［23］Wang Z， Bovik AC， Sheikh HR， etal. Image quality assessment：from error measurement to structural similarity［J］.IEEE Trans on Image Processing，2004，13（4）：600 －612.