CCM模式下非理想Buck变换器的建模与仿真*

宣 传，徐慧芳，解光军

(合肥工业大学电子科学与应用物理学院，合肥230009)

随着DC-DC变换器技术的迅猛发展，对开关电源的建模方法提出了更高的要求。电路中的很多非理想因素都要考虑，为了能用理想变换器的建模方法，建模前的一些理想化处理变得非常重要。考虑滤波电容串联等效电阻后，会在控制-输出传递函数上附加一个高频零点，这个高频零点会影响开关调节系统的稳定性，所以必须引入补偿网络，对这个高频零点进行抵消。

1 非理想Buck变换器等效电路

Buck变换器考虑其非理想寄生参数［1-3］的等效电路如图1所示，其中有源开关功率MOSFET等效为开关S和导通电阻RS的串联，二极管D等效为开关D、正向压降VD和导通电阻RD的串联，RL、RC分别为滤波电感L、滤波电容C的等效串联电阻。假设开关元件S的开关周期为TS，导通时间为Ton，则占空比D=Ton/TS。

图1 考虑寄生参数的非理想Buck变换器等效电路

对于CCM模式下考虑电感电流纹波影响的非理想Buck变换器，流过电感以及两个开关管上的电流波形如图2所示。

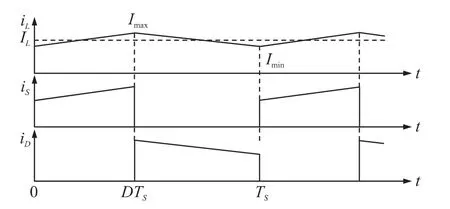
图2 CCM模式下Buck变换器各电流波形

设电感电流iL(t)在一个开关周期内的最大值为Imax，最小值为Imin，则电感电流iL(t)可以表示为:

设电感电流在一个开关周期内的平均值为IL，则有:

电感电流纹波为:

则电感电流在一个开关周期内的有效值为:

电感等效串联电阻RL的导通损耗功率为:

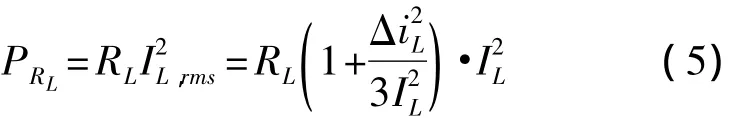
所以，根据能量守恒原理，电感等效串联电阻RL在一个开关周期内的等效电阻为:

用相同的方法便可以得到有源功率开关管S的导通电阻RS和续流二极管D支路中寄生电阻RD折算到电感支路中的等效平均电阻

将续流二极管D支路中寄生电压VD折算到电感支路中的等效平均电压为:

电感L本身的等效串联电阻为RL，最后将电感支路上三个串联等效寄生电阻合并，得到电感支路上总的等效平均电阻为:

至此，已经根据能量守恒原理，求出两个开关元件寄生参数的等效平均值，并将他们折算到电感支路中，此时的Buck变换器等效电路模型如图3所示。

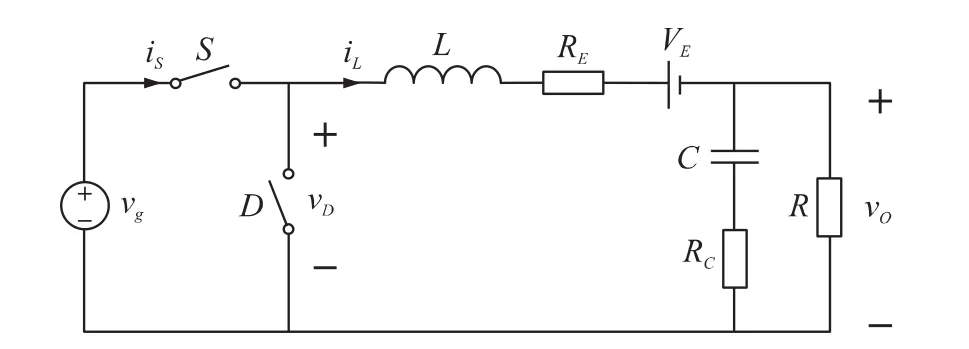
图3 等效变换后的CCM模式下非理想Buck变换器等效电路模型

2 用开关网络平均模型法建模

图3可以用理想的开关管Q1和二极管D1分别来代替电路中的开关S、D，就可以得到非理想Buck变换器等效电路模型［4-7］，如图4所示。

图4 用理想开关器件代替开关S、D后的Buck变换器

变换器中包含的Q1和D1两个理想开关元件组成了一个开关网络，形成一个二端口，如图4中虚线框所示，端口电压电流分别为vg、is、vD、iL。选择iL与vg作为二端口的独立变量，is与vD作为非独立变量。当变换器满足低频假设与小纹波假设时，非独立变量的平均变量可以用独立变量的平均变量表达为

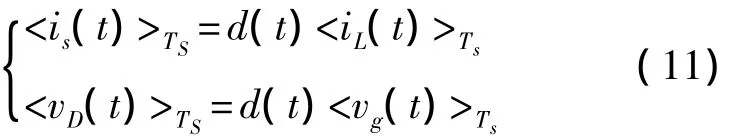
由式(11)可以建立由受控源构成的变换器的平均等效电路，即变换器的大信号等效电路，如图5所示。

图5 非理想Buck变换器平均变量等效电路

令图5中的各平均变量等于其对应的直流分量，得到其直流等效电路，其中的一对受控源的作用相当于一个理想变压器(可以变换直流)，再使电路中的电感短路、电容开路，电路中的瞬时值变量用其直流量表示，就可以得到非理想Buck变换器直流等效电路，如图6所示。

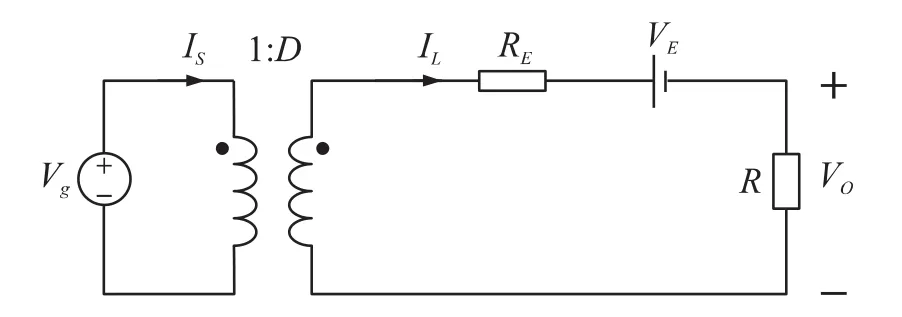
图6 非理想Buck变换器的直流等效电路模型

由图6所示电路，以及式(9)、式(10)，可得

因此，若要提高变换器的效率，必须满足RE≪R，VE≪Vo，即选择导通电阻RS较小的有源开关功率MOSFET，正向压降VD和导通电阻RD都较小的二极管D。对于式(12)和式(13)，若不考虑非理想寄生参数，则Vo=DVin，η=100%，即为理想Buck变换器。

在图5的基础上，对开关网络平均变量等效电路中的各平均变量分离扰动，分解为相应的直流分量和交流分量之和，忽略其中的高阶微小量，并消去相应的直流量，可以得到开关电源的交流小信号等效电路，如图7所示。

图7 CCM模式下非理想Buck变换器的交流小信号等效电路模型

对于图7所示的交流小信号等效电路，对各参数s进行域变换，计算出输出电压(s)对控制变量(s)的传递函数Gvd(s):

3 带电压反馈的非理想Buck变换器

开环系统会因为输入电压或者负载的变化出现不稳定现象，所以在图7基础上增加一个电压反馈回路［8-9］，如图8所示，它是一个单环自动调节系统，这种控制方式简单、稳定、易于设计，也可以保证很好的稳压精度。

图8 具有反馈环的Buck变换器小信号模型

因此，其开环传递函数为

根据式(14)，在非理想情况下，考虑了滤波电容C的等效电阻后，会引入一个零点，其零点频率为ωz0，为了抵消其带来的影响，我们在补偿网络中就必须引入一个极点。在实际设计变换器中，PID补偿器在低频时，增大低频环增益，实现输出电压低频分量的精确调节;高频时(增益交越频率附近)，改善相位裕度。因此，采用图9所示的PID补偿网络。

图9 PID补偿器网络(C2≫C1，R1≫R3)

根据电路图可以写出补偿网络的传递函数及有关公式

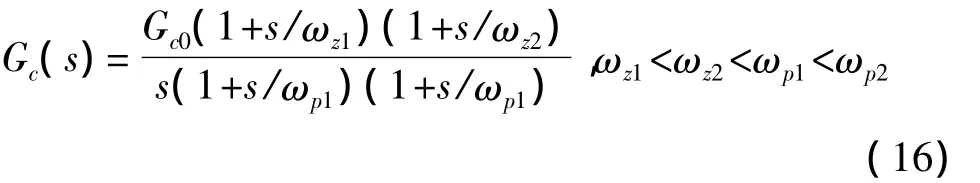
则补偿后的开环传递函数为:

4 电路参数设计与仿真分析

本文选用的设计实例中Buck变换器各参数为:Vg=15 V，Vo=10 V，R=10 Ω，L=127 μH，RL=0.72 Ω，C=247 μF，RC=20 mΩ，RS=10 mΩ，RD=30 mΩ，V0=0.45 V，Vref=5 V，电感电流纹波 ΔiL=0.06 A，开关频率fs=50 kHz，PWM输出的峰值Vm=1 V。

由式(10)和式(12)算出模型的各个参数为:IL=1 A，D=0.7240，RE=0.7346 Ω。为了提高穿越频率，设加入补偿器后开环传递函数的穿越频率fc是开关频率fs的1/5，即

第1步 选择采样网络

由于H(s)V0≈Vref，若Vref=5 V，则

第2步 计算主电路的传递函数

根据式(14)计算得到

其中Gd0=13.97，ωz0=202400 rad/s，ωp0=5844 rad/s，Q=0.9194。

第3步 补偿网络的参数确定

将H(s)，VM代入得补偿后的开环传递函数为

为了抵消控制对象传输函数中双重极点引起的相位滞后，设置补偿网络的两个零点均为

第1个极点fp1用来抵消输出电容ESR引起的零点fp0，则有

第2个极点fp2用来增加高频衰减率，其值取为

由|T(jωc)|dB=0 dB 得

得

因此，系统开环传递函数为:

5 仿真分析

为了验证非理想基本变换器在连续工作模式(CCM)下的电路平均建模方法的正确性，并将其与原有建模方法进行定量比较，利用 MATLAB软件［10］对实际Buck变换器进行了系统的小信号特性仿真研究，如图10所示，①、②、③分别对应以下情况:①.RE=0.74 Ω，RC=0.02 Ω，即考虑变换器所有的寄生参数;②.RE=0，RC=0.02 Ω，即只考虑滤波电容的等效串联电阻;③.RE=0，RC=0，即考虑变换器理想情况。由式(14)和图10得，RE增大，占空比D增大，Gvd曲线的转角频率ωp0增大，品质因数Q减小，谐振峰值减小，振荡环节的相角变化减慢。验证了Buck变换器在连续工作模式(CCM)下开关网络平均建模方法的正确性，揭示了考虑寄生参数建模的必要性。

图10 CCM模式下Buck变换器传递函数波特图(点状线、虚线、实线分别对应①、②、③三种情况)

再对变换器补偿前后进行仿真，如图11所示。其中虚线代表补偿前的图形，实线代表补偿后的图形。根据仿真结果补偿前的穿越频率ω'c=22202 rad/s，相位裕量 ρ'm=23.36°＜45°，从表面上看，系统是稳定的，但是如果系统的参数稍有变化，体统可能变得不稳定，且穿越频率太低，系统的响应速度很慢。加入了PID补偿网络后穿越频率 ωc=62712 rad/s，相位裕量 ρm=56.85°，所以元件稍有变化，穿越频率只会稍稍偏离，对相位裕量影响较小。而且在低频段，补偿前的曲线是一条水平线，所以系统的稳态误差很大，由于补偿网络在直流处提供了一个极点，因此补偿后的曲线稳态误差等于零。高频段，补偿后的曲线是-40等于dB/dec的斜率下降，能够有效地抑制高频干扰。因此设计的补偿电路基本符合要求。

图11 补偿前、后传递函数Bode图(实线、虚线分别对应补偿后、补偿前的情况)

6 结论

本文主要介绍了运用基本的能量守恒定律将非理想Buck变换器经过换算变化后，适用于用理想的模型来解决建模问题的一个方案。由仿真结果可以得到引入补偿器后，系统的稳态增益、带宽、相位裕量增大，稳态精度、瞬态响应速度、稳定性得到提高，抗负载扰动和抗输入电压扰动的抑制能力得到加强。验证了模型的正确性及建模对电路设计的指导意义。

［1］张卫平.开关变换器的建模与控制［M］.北京:中国电力出版社，2006.

［2］Czarkowski D，Kazimierczuk M K.Energy-Conservation Approach to Modeling PWM DC-DC Converters［J］.IEEE Trans Aerosp Electron Syst，1993，29(3):1059-1063.

［3］Davoudi A，Jatskevich J.Realization of Parasitics in State-Space Average-Value Modeling of PWM DC-DC Converters［J］.IEEE Trans Power Electronics，2006，21(4):1142-1147.

［4］张卫平.DC/DC变换器稳态建模的教学方法［J］.电气电子教学学报，2008，5:101-104.

［5］Lineykin S，Ben-Yaakov S.Unified SPICE Compatible Model for Large and Small-Signal Envelope Simulation of Linear Circuits Excited by Modulated Signals［J］.IEEE Trans.Industrial Electronics，2006，53(3):745-751.

［6］Lin J L，Chang C H.Small-Signal Modeling and Control of ZVTPWM Boost Converters［J］.IEEE Trans.Power Electronics，2003，18(1):2-10.

［7］Nisha Kondrath，Marian K Kazimierczuk.Comparison of Wide-Frequency and High-Frequency Duty Ratio-to-InductorCurrent Transfer Functions of DC-DC PWM Buck Converter in CCM［J］.IEEE Transactions on Industrial Electronics，2011(3):1-4

［8］程心.非理想DC-DC开关变换器的建模分析与仿真［D］.合肥:合肥工业大学，2009.

［9］Young Ik Son，In Hyuk Kim.Complementary PID Controller to Passivity-Based Nonlinear Control of Boost Converters With Inductor Resistance［J］.IEEE Transactions on Control Systems Technology，2011(4):1-9

［10］(英)Marty Brown，著.徐徳鸿，沈旭，杨成林，等译.开关电源设计指南(原书第二版)［M］.北京:机械工业出版社，2004:54-149.