二维正方晶格光子晶体的带隙研究*

袁秀娟，潘 鸣，曹 威

(1.杭州电子科技大学电子学院，杭州310018;2.中国电子科技集团公司第五十研究总体部，上海200063;3.西安外事学院工学院，西安710077)

太赫兹(THz，1 THz=1012Hz)这一概念是Fleming在1974年提出来的，泛指频率在0.1 THz～10 THz这一波段内的电磁波［1］。该段电磁波，在电磁波谱上位于微波和红外波之间，被称为亚毫米波和远红外波。1 THz光子的等效温度为48 K，因此自然界广泛存在THz射线。由于THz的低能性，高透性，以及其丰富的指纹谱性［2-4］，THz已经引起了科学界的广泛关注［5］。THz特性的研究及其开发利用与各种操控THz波的光学器件密不可分，THz研究的不断发展对这些器件提出了很大的需求。在这种情况下，“光子晶体”这一特殊材料应运而生。光子晶体的概念，于1987年由S.John和E.Yablonovitch分别提出，是指由两种或两种以上介质周期排列所构成的人造晶体［6-7］。光子晶体最重要的特征就是具有光子禁带，凡是频率落在禁带中的光，不论其波矢和偏振方向如何，都会被严格禁止传播。利用这一特性可以将其应用于THz波段的电磁波传输和滤波，且具有色散小、损耗低等优点，可以制作出多种品质优良的THz器件。

本文利用平面波展开法［8-11］(PWM)分析研究了正方晶格THz光子晶体的禁带特性。平面波展开法主要是将电磁场在倒格矢空间以平面波叠加的形式展开，将Maxwell方程化成一个本征方程，然后求解本征值即可得到传播光子的本征频率，从而获得光子晶体的光子禁带。

1 理论和计算方法

THz波在二维正方晶格光子晶体中的传输特性可用Maxwell方程来描述。传播方程如下:

图1(a)为介电常数为εa的介质圆柱嵌在介电常数为εb中材料中所构成的二维正方晶格光子晶体的截面图。介质柱半径为r，晶格常数为a。图2为正方晶格的第1 Brilliouin区。二维光子晶体中，入射电磁波可以分解为E偏振和H偏振，即电场平行于介质柱的TM模和磁场平行于介质柱的TE模。

图1 二维正方晶格光子晶体

由二维光子晶体的周期性，可以把ε-1(x11)，H3(x11，ω)展开成傅里叶级数

其中K是被限制在第1 Brillouin区域的波矢量。

首先考虑H偏振，此时H和E可写成:

其中x11为坐标轴所构成的平面上的矢量。把式(5)和式(6)代入式(2)，消去E1和E2，可以得到H3的表达式:

再把式(3)和式(4)代入式(7)可得:

由式(8)可看出，对TE偏振的电磁波在光子晶体中的传播问题就变成了求解对称矩阵的本征值和本征函数的问题。

同理可得E偏振的方程如下:

式(8)和式(9)分别是对无限多个倒格矢的求和。文中采用N个倒格矢的和来近似代替。因此这两个方程分别变成含有2N×2N个矩阵元的本征值方程，可以采用数值计算的方法来求解。

考虑到每个原胞都分别由介质为εa和εb的两种材料组成，因此上两式中的系数可表示为:

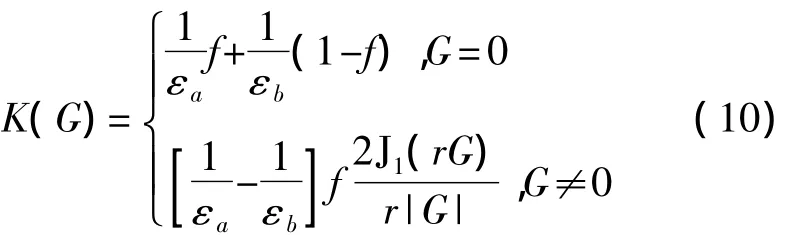
其中J1为一阶贝塞尔函数;f为填充因子，表明介质柱或空气柱占整个晶胞的百分比，对于正方晶格，f的表达式为:

将式(10)代入式(9)和式(8)，即可求出H偏振和E偏振的本征频率。

2 数值计算结果与分析

计算采用的模型如图1所示，介质柱的相对介电常数为εa，背景的相对介电常数为εb。计算时，采用441个平面波进行展开。

2.1 介质柱半径对光子带隙的影响

选用的晶格常数为a=0.1 mm，介质的相对介电常数为εa=11.6，背景的相对介电常数为εb=1，在固定介电常数和晶格常数不变的情况下，改变介质柱的半径，使其半径从0.2a变化到0.4a，通过大量仿真数据，分析TM模式和TE模式下光子晶体的带隙变化规律。图2(a)、2(b)以及2(c)分别为r=0.2a，r=0.3a，以及r=0.35a时，光子晶体TM模式下的带隙分布图。图3(a)、3(b)以及 3(c)分别为r=0.2a，r=0.3a以及r=0.35a时光子晶体TE模式下的带隙分布图。

图2 TM模式下正方晶格光子晶体带隙分布图(εa=11.6保持不变)

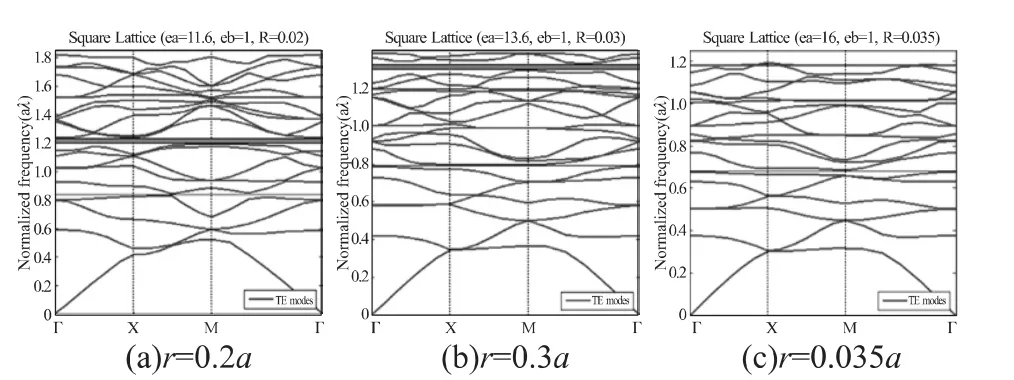
图3 TE模式下正方晶格光子晶体带隙分布(εa=11.6保持不变)

从表1中给出的数据可以看出，在TM模式下，当保持介质柱相对介电常数不变时，随着介质柱半径的增大，第1带隙的带宽慢慢变小;随介质柱半径的增大，带隙的数量增多，出现第2、第3等多个带隙，且第2带隙的宽度将慢慢超过第1带隙;随介质柱半径的增大，所有带隙都往频率低端移动。

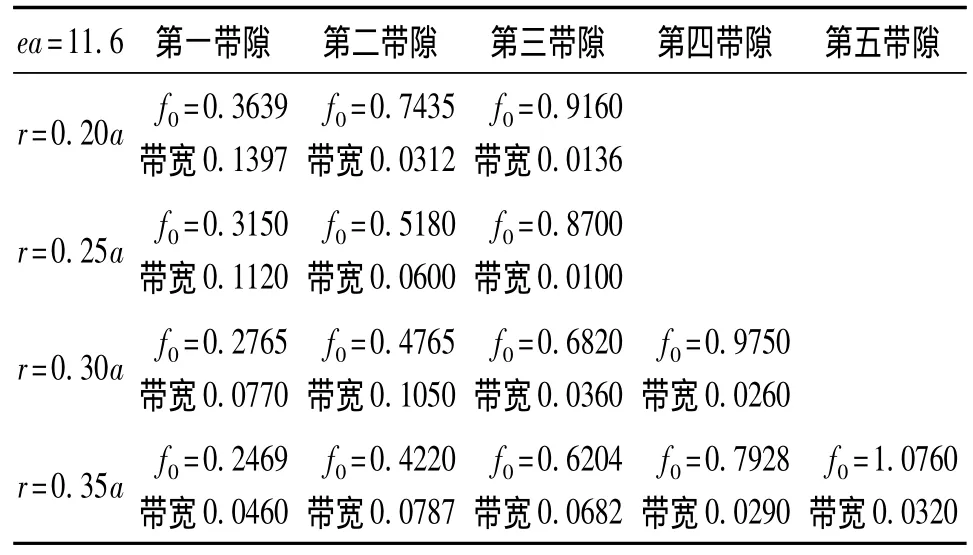
表1 TM模式下不同介质柱半径的光子晶体的带隙分布THz

从表2中给出的数据可以看出，在TE模式下，当保持介质柱相对介电常数不变时，随着介质柱半径的增大，第1带隙的带宽慢慢变小;随介质柱半径的增大，带隙的数量慢慢减少;随介质柱半径的增大，第1带隙往频率低端移动。

表2 TE模式下不同介质柱半径的光子晶体的带隙分布THz

比较TM模式和TE模式可以发现，TM模式比较容易出现带隙，出现带隙的数量差别比较大;在TM模式情况下，带隙数量随着介质柱半径的增大而增多，而TE模式情况下，带隙数量随着介质柱半径的增大而减少;在TM模式下，带隙的带宽较宽，比较容易实现带内滤波的功能。

2.2 介电常数对光子带隙的影响

选用的晶格常数为a=0.1 mm，介质柱的半径r=0.2a，介质的相对介电常数为分别选取了εa=11.6，εa=13.6，εa=16和εa=20共四组数据，固定晶格常数和介质柱半径不变的情况下，改变介质柱的相对介电常数，使其值从εa=11.6变化到εa=20，通过大量仿真数据，分析TM模式和TE模式下光子晶体的带隙变化规律。图4(a)、4(b)和4(c)分别为 εa=11.6，εa=13.6和εa=16时光子晶体TM模式下的带隙分布图。图5(a)、5(b)和5(c)分别为εa=11.6，εa=13.6和εa=16时光子晶体TE模式下的带隙分布图。

图4 TM模式下正方晶格光子晶体带隙分布图(r=0.2a保持不变)

图5 TE模式下正方晶格光子晶体带隙分布图(r=0.2a保持不变)

从表3中给出的数据可以看出，在TM模式下，当介质柱的半径保持不变时，随着介质柱相对介电常数的增大，第1带隙的带宽慢慢增大;随介质柱相对介电常数的增大，带隙的数量增多，出现第2、第3多个带隙，但第1带隙的宽度仍是最大的;随介质柱相对介电常数的增大，所有带隙都往频率低端移动。

表3 TM模式下不同介质柱相对介电常数的光子晶体的带隙分布 THz

从表4中给出的数据可以看出，在TE模式下，当介质柱的半径保持不变时，随着介质柱相对介电常数的增大，带隙的数量慢慢减少;随介质柱相对介电常数的增大，所有带隙都往频率低端移动;随介质柱相对介电常数的增大，最大带隙的带宽慢慢减小;中心频率最高的带隙为主要带隙，带宽最大。

表4 TE模式下不同介质柱相对介电常数的光子晶体的带隙分布 THz

比较TM模式和TE模式可以发现，TM模式比较容易出现带隙;在TM模式情况下，带隙数量几乎不变，而TE模式情况下，带隙数量随着介质柱半径的增大而减少;在TM模式下，带隙的带宽较宽，比较容易实现带内滤波的功能。

3 结论

本文研究了THz波段的二维正方晶格光子晶体，理论研究发现，在特定的晶格常数下，改变介质柱的参数如介质柱的半径大小或者介质柱的相对介电常数，都会引起光子带隙的带宽、中心频率以及带隙数量的相应改变，且呈现一定的规律性。这一结论对制作特定波段的光子晶体滤波器、波导等器件，具有实际应用价值。

［1］Fleming J W.High-Resolution Submillimeter-Wave Fourier-Transform Spectrometry of Gases［J］.IEEE Transactions on Microwave Theory and Techniques，1974，22(12):1023-1025.

［2］许景周，张希成.太赫兹科学技术和应用［M］.北京:北京大学出版社，2007.

［3］王少宏，许景周，汪力，等.THz技术的应用及展望［J］.物理，2001，30(10):612-615.

［4］张存林，张岩，赵国忠，等.太赫兹感测与成像［M］.北京:国防工业出版社，2008.

［5］姚建铨，路洋，张百刚，等.THz辐射的研究和应用进展［J］.光电子·激光，2005，16(4):503-510.

［6］John S.Strong Localization of Photonic in Certain Disordered Dielectric Superlattices［J］.Phys.Rev.Lett.，1987，58(23):2486.

［7］Yablonovitch E.Inhibited Spontaneous Emission in Solid-State Physics and Electronics［J］.Phys.Rev.Lett.，1987，58(20):2059-2062.

［8］Plihal M，Maradudin A A.PhotonicBand StructureofTwo-Dimensional Systems:The triangular latticce［J］.Phys.Rev.B，1991，44(16):8568-8571.

［9］Ho K M，Chan C T，Soukoulis C M.Existence of a Photonic Gap in Periodic Dielectric Structures［J］.Phys.Rev.Lett，1990，65(25):3152-3155.

［10］Gassagne D，Jouanin C，Bertho D.Hexagonal Photonic-Band-Gap Structures［J］.Phys.Rev.B，1996，53(11):7134-7142.

［11］Kazuaki Sakoda.Optical Transmittance of a Two-Dimensional Triangular Photonic Lattice［J］.Phys.Rev.B，1995，51(7):4672-4675.