基于Matlab的小波去噪算法研究

齐 敏，黄世震

(福州大学福建省微电子集成电路重点实验室，福州350002)

信号去噪［1-2］是信号分析中的一个重要组成部分。传统的数学工具是短时傅里叶变换，是建立在传统傅里叶变换上的滤波方法，这种方法在提高信噪比和提高空间分辨率这两项信号分析的指标上存在矛盾。而小波分析［3-12］在时频分辨率特征、多分辨率分析、小波包、突变信号检测、快速小波分析等方面有独特的表现。

1 小波变换的定义及性质

1.1 小波变换的定义

小波分析就是将原始信号展开成一族小波基函数的加权和，这族基函数由一个由带通函数经过平移和变化比例得到。

在连续的情况下，小波函数的定义为:

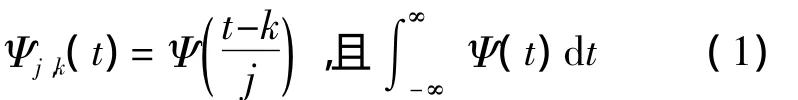
其中Ψ(t)称为基小波，j为伸缩因子，k为平移因子。Ψa，b(t)为基小波有平移、缩放构成的小波信号。

因此，对于连续信号f(t)的连续小波变换公式为:

其反变换的定义为:

在离散的情况下，小波函数的定义为:

设函数 φj，k(k)∈L2(IR)，对于任意一个平方和积函数f∈L2(IR)，其二进制小波变换定义成函数序列{W2jf(k)}k∈Z}，其中

小波变换系数W2j(k)给出了f(x)的尺度2j在位置k住的逼近。其反变换的定义为:

1.2 多分辨率分析与Mallat算法

在实际应用中，为了提高小波变换的计算速度，经常采用的方法是基于多分辨率分析的Mallat快速算法。多分辨率分析的实质是将信号分解到一系列不同频率的空间上，信号在不同的尺度上的多分辨分析，可以显示信号不同频率的特征。每次分解都将信号分解成低频和高频两个部分。对低频部分再进行分解，得到更高尺度上的低频和高频部分。分解的尺度越高，分解得到信号的频率就越低。以信号的3层分解为例，如图1所示。由此得到信号S=ca3+cd3+cd2+cd1。可以看到，多分辨分析的实质就是对低频空间做进一步分解，最终让频率的分辨率越来越高。

图1 信号的三层小波分解示意图

Mallat算法的小波分解公式为:

其中，n=0，1，2，…，N-1，N为输入序列的长度，cmj是分解得到的低频分量，是分解得到的高频分量;j表示第j级小波分解，j=0，1，2，…，M，其中必须满足2M＜N。特别，当j=0时，cn0表示的就是输入序列fn;m为每次小波分解后低频与高频分量的长度，m、n伴随小波分解级数j的增加逐渐减小;hn-2m为多分辨率分析的尺度系数，gn-2m为多分辨分析的小波系数。

由式(7)、式(8)可得，输入的离散序列cn0与固定系数hn-2m和gn-2m进行m次乘积累加之后得到的是第1级分解的低频分量cm1和高频分量dm1，然后cm1作为第2级分解的输入序列，经过分解后得到cm2和，依此类推得到第M级分解后的cmM和dmM。小波重构与小波分解在过程上正好是相反的。

2 基于阈值的小波去噪

由于在实际的工程应用中，有用信号通常为低频信号。噪声信号通常为高频信号。所以信号经过小波分解之后，噪声信号基本包含在 cd1、cd2、cd3中。因此，通过多分辨率分析得到的高频率的小波系数，经过门限阈值等新式进行相应处理，再重新构造出输入序列，就可以实现信号去噪的效果。

一般而言，一维信号的小波去噪可通过以下3个步骤实现。

(1)将一维信号进行小波分解 选择合适的小波分解层次N，对输入信号s(i)进行N层的小波分解;

(2)小波分解的高频系数阈值量化 选择一个适当的阈值对第1层至第N层的小波高频系数进行阈值量化处理;

(3)一维小波重构 由得到第N层的低频小波系数与量化之后的第1层至第N层高频小波系数经过小波重构后得到去噪后的一维信号。

上述3个步骤中，直接对信号去噪有重大影响的，就是阈值的选择以及如何进行阈值的量化两个方面。

2.1 传统的阈值量化方法

传统的阈值处理方法通常有两种:

硬阈值法:

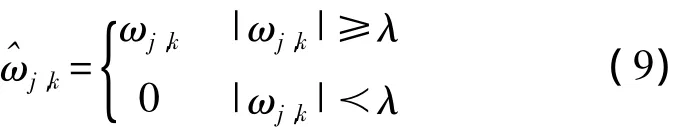
软阈值法:

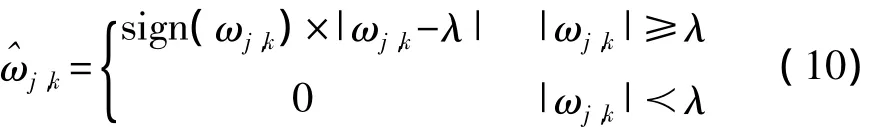
其中，ωj，k为小波系数，为量化后的小波系数，λ为阈值，一般的。图2和图3分别表示硬阈值方法和软阈值方法。两种方法在实际中虽然都得到较多的应用，同时也取得了较好的去噪效果，但是依然存在许多问题。例如，在硬阈值法中，在λ处不是连续的，所以在信号重构过程中可能使重构信号产生振荡;在软阈值法中，虽然量化得到具有较好的连续性，但当||＞λ时，与ωj，k存在一个恒定的偏差，这也使得重构信号与真实信号的近似性有一定的影响。所以，就需要有一种新的阈值处理方法，既可以改正上述两种方法的不足之处，又可以进一步提高信号的去噪效果。

图2 硬阈值法

图3 软阈值法

2.2 改进的阈值去噪方法

要达到改进上述两种阈值方法，只需要在阈值函数中引入一个参数α即可:

上式即称为软硬阈值折衷法的阈值函数。特别当α分别取0和1时，上述方法即分别变换成为硬阈值方法和软阈值方法。所以，当取0＜α＜1时，由该方法量化得到的的数值介于硬、软两种方法之间。此方法模型如图4所示。

图4 软、硬阈值折衷法

该方法思路简单，去噪效果好。通过分析图4不难发现，单纯使用软阈值方法量化得到^ωj，k的绝对值比 ωj，k小 λ(|ωj，k|≥λ)。所以在实际应用中就要减少这一偏差，如果这个偏差减小到0(即使用硬阈值方法处理)，也不能实现最好的去噪效果，因为ωj，k本身由有用信号的高频部分和噪声信号组成，可能会由于噪声信号的影响导致重构信号产生更大的偏差。因此，在量化函数中引入一个参数α，使量化结果介于硬阈值量化和软阈值量化之间，就可以让重构信号更接近真实信号。所以基于这一思想，只要适当调整α的取值，就可以得到很好的去噪效果。

3 基于Matlab的实验仿真

为了更加直观的比较不同阈值方法的去噪效果，引入信噪比定义:

其中，f(i)为真实信号，s(i)为含噪信号，L为信号长度。

在仿真实验中，选用雷达回波信号［13-15］作为实验信号，噪声采用的是高斯白噪声与服从相关对数-正态分布的随机数两种组合，模拟实际中雷达测距的噪声，选取db4小波作为小波基，小波分解尺度为4，α取0.65。通过对比不同阈值处理方法的信噪比来比较不同方法去噪的效果。

由于雷达信号的特殊性，即回波信号与噪声信号大致相当。因此在选择噪声时，使用服从相关对数-正态分布的随机数模拟雷达信号噪声中的地物噪声，用高斯白噪声模拟实际雷达系统中的热噪声。图5是忽略系统内部热噪声的去噪效果比较，图6则是综合考虑所有噪声的去噪效果比较。从表1中可以看到，软硬阈值折衷法进行去噪后在信噪比上要明显优于单纯使用软阈值法或硬阈值法。

图5 添加随机数噪声的去噪结果

图6 添加白噪声和随机数噪声的去噪结果

表1 各阈值去噪方法的信噪比的比较

本实验的λ选择方式是采用极大值极小值原理选择信号消噪的阈值，产生一个最小均方误差的极值。这里λ的选取方式虽然不是最优的，如果λ选取方式更加恰当，就更加可以体现出改进的方法的优越性。

4 结束语

本文介绍了小波阈值降噪的基本原理和实现的具体步骤。讨论了软、硬阈值法以及改进的阈值去噪方法，并且通过实验对上述三种方法的去噪效果进行了比较。可以看到在改进的阈值去噪方法的去噪效果要好于传统的去噪方法。同时，由于本文选取的λ值并非最佳，如λ选取得当，即可得到更好的结果。不过，本文通过实验已经可以发现，不论λ取值如何，折衷法的计算结果都要由于软阈值与硬阈值各自独立的方法。

［1］王嘉梅.基于Matlab的数字信号处理与实践开发［M］.西安:西安电子科技大学出版社，2007.

［2］张德丰.MATLAB数字信号处理与应用［M］.北京:清华大学出版社，2010.

［3］胡昌华.基于Matlab的系统分析与设计——小波分析［M］西安:.西安电子科技大学出版社，1999.

［4］Stephane Mallat.信号处理的小波导引［M］.第2版.北京:机械工业出版社，2002.

［5］王亚，吕新华，王海峰.一种改进的小波阈值降噪方法及Matlab实现［J］.微计算机信息，2006，22(6):259-261.

［6］赵海英，纪超辉.小波变换降噪技术及其在Matlab中的实现［J］.兵工自动化，2006，25(2):54-55.

［7］李祥兵，肖合林.基于Matlab的小波阈值折衷去噪算法研究［J］.电脑开发与应用，2009，22(6):4-6.

［8］史振江，安建龙，赵玉菊.基于 Matlab的小波小赵仿真实现［J］.石家庄铁路职业技术学院学报，2008，7(1):63-66.

［9］Quan Pan.Two Denoising Methods by Wavelet Transform［J］.IEEE Transaction on Signal Processing，1999，47(12):3401-3405.

［10］李佳升，黄文清，戴瑜兴.基于自定义阈值函数的小波去噪算法［J］.电力系统保护与控制，2008，25(2):21-24.

［11］郭晓霞，杨慧中.小波去噪中软硬阈值的一种改良折衷法［J］.智能系统学报，2008，3(3):222-225.

［12］Dong Yongsheng，YI Xuming.Wavelet De-Noising Based on Four Improved Functions for Threshold Estimation［J］.Journal of Math，2006，19(2):534-540.

［13］Mahafza B R，Elsherbeni A Z.MATLAB Simulations for Radar Systems Design［M］.北京:电子工业出版社，2009.

［14］许小剑，黄培康.雷达系统及其信息处理［M］.北京:电子工业出版社，2010.

［15］刘波，文忠，曾涯.MATLAB信号处理［M］.北京:电子工业出版社，2006.