基于相对速度偏角的舰空导弹三维制导律设计
赵永涛,胡云安,耿宝亮,戴卫祥
(1.海军航空工程学院 控制工程系,山东 烟台264001;2.92060部队 军械教研室,辽宁 大连116000)
舰空导弹的飞行末端一般采用比例导引律,但当目标做大机动飞行时,会产生较大的脱靶量.而修正比例导引律、最优导引律和微分对策导引律为达到尽可能小的脱靶量,需要引入各种准确的测量信息,尤其需要的是目标机动加速度、导弹剩余飞行时间等信息,这大大增加了导引律在工程实现上的复杂性[1~4].
鉴于变结构控制对外界干扰和参数摄动的强鲁棒性,很多文献都对变结构导引律进行了研究,且选取弹目视线角速度或弹目相对距离作为滑模面[5~8].考虑到视线角速度随相对距离的减小会急剧变化,并且采用视线角速度或相对距离作为零化目标的导引算法不能适用于任意初始导弹和目标方位角,为此,文献[9~11]针对平面拦截情况,在平面内选择导弹与目标的相对速度偏角作为零化目标,设计了基于零化相对速度偏角的二维末制导律,但未对基于零化相对速度偏角的空间制导律进行研究.本文针对舰空导弹空间拦截掠海大机动目标问题,在建立三维空间导弹拦截目标相对运动模型的基础上,对空间拦截情况下的相对速度偏角进行了定义,并选取空间相对速度偏角作为滑模面,设计了一种基于零化相对速度偏角的空间三维变结构末制导律,并给出了导引指令信息解算模型,仿真结果验证了在对抗目标大机动和低空目标视线角速度量测噪声等方面,所设计导引律比传统的空间末制导律具有更强的鲁棒性.
1 三维空间导弹拦截目标模型的建立
三维空间中导弹拦截目标的相对运动关系如图1所示.

图1 三维拦截几何图
图1中,MXcYcZc为参考坐标系(简称c系),MXmYmZm为导弹弹道坐标系(简称 m系),TXtYtZt为目标弹道坐标系(简称t系),MXLYLZL为视线坐标系(简称L系).(εL,βL)是参考坐标系到视线坐标系转换的欧拉角,即视线高低角和视线方位角;(εm,βm)是视线坐标系到导弹弹道坐标系转换的欧拉角;(εt,βt)是视线坐标系到目标弹道坐标系转换的欧拉角;M和T分别代表导弹和目标,R为导弹与目标之间的相对距离.
假定导弹和目标均作质点运动,vm和vt分别为导弹与目标的速度(用vm,vt分别表示其数值大小);am,at分别为导弹与目标的加速度.
由图1,建立导弹和目标相对运动的空间矢量方程:
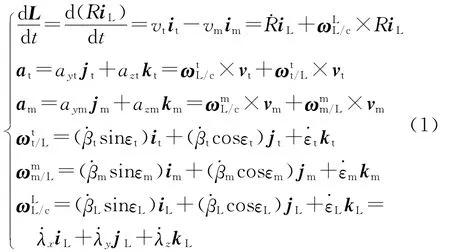
式中:i,j,k为坐标系各轴对应的单位矢量;ω为视线角速度矢量,L/c表示L系相对c系旋转,上标L表示在L系的投影;ayt,azt分别为目标加速度at在t系jt轴和kt轴的投影;aym,azm分别为导弹加速度am在m系jm轴和km轴的投影.
对式(1)的矢量方程进行变换和推导后[2],可以得到三维空间导弹拦截目标的相对运动学关系:

2 基于零化相对速度偏角的三维变结构末制导律设计
2.1 空间拦截相对速度偏角定义
设导弹与目标的相对速度用vr表示,定义为vr=vt-vm.建立相对速度坐标系MXrYrZr(简称r系):原点为导弹质心;MXr轴指向相对速度的正向;MYr轴在包含MXr轴的铅垂面内,垂直于MXr轴,向上为正;MZr轴垂直于MXrYr平面,其方向按右手定则确定.相对速度坐标系与视线坐标系的关系如图2所示.
图2中,εr称为相对速度偏角高低角,定义为相对速度vr与其在视线坐标系MXLYL的投影之间的夹角,若相对速度在MXLYL面之上,则εr为正,反之为负.βr为相对速度偏角方位角,定义为相对速度vr在视线坐标系MXLYL的投影与视线坐标系MXL轴之间的夹角.由MXL轴逆时针方向转至相对速度在视线坐标系MXLYL的投影线时,βr为正,反之为负.

图2 相对速度坐标系和视线坐标系
视线坐标系到相对速度坐标系转换矩阵CrL为

2.2 导引律设计
假设导弹与目标相对加速度为ar,由相对速度的定义,相对加速度空间矢量方程为

由图2,得:


将式(11)和式(12)代入到式(10),并令ar=(arxaryarz)T,可得:

由式(10),有

式中,

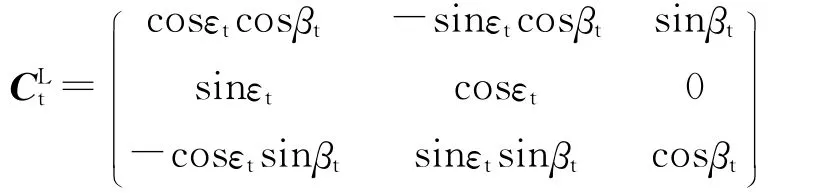
式(13)~式(15)即为相对速度偏角角速度与导弹和目标加速度之间的关系表达式.
选取滑模面:

选取趋近律为

式中,k1>0,ζ1>0,k2>0,ζ2>0.
对式(16)求导,并由式(13)和式(15),结合式(18),得:

式中,

对式 (17)求导,由 式 (14)、式 (15),并结合式(19),得:
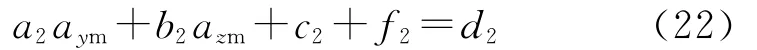
式中,

由式(20)和式(22),并将目标加速度和方位信息视为干扰量,解得导弹俯仰通道指令aym和偏航通道指令azm分别为

2.3 指令信息解算模型
由2.2节的导引指令式(24)和式(25)可见,实现基于零化相对速度偏角的三维制导律需要(,,,εm,βm,vr,εr,βr)信 息.其 中 ,(,,)由 末制导雷达导引头提供,而(εm,βm,vr,εr,βr)需要通过解算获得.下面给出(εm,βm,vr,εr,βr)信息的解算模型.
选取参考坐标系为地面坐标系OXdYdZd(简称d系).其定义为:与地球固联,原点取飞行器质心在水平面上的投影,OXd轴在水平面内,指向目标为正;OYd轴与地面垂直,向上为正;OZd轴按右手定则确定.εL,βL由末制导雷达导引头提供;θm,ψvm分别为导弹弹道倾角与弹道偏角,由弹载惯性测量装置提供.导弹速度视线坐标系的投影为
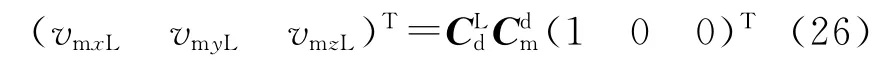
式中,

εm和βm的解算如下:
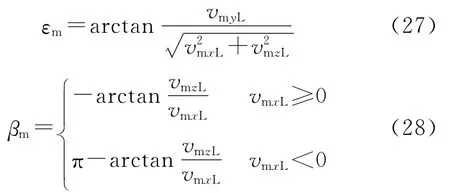
设相对速度矢量vr在视线坐标系的投影为(vrxLvryLvrzL)T,由相对速度的定义得:
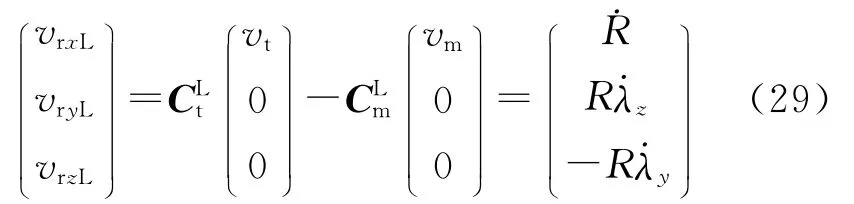
由式(29),可得相对速度:

相对速度偏角高低角:

相对速度偏角方位角

3 仿真分析
设定仿真参数为:导弹初始位置(xm,ym,zm)为(0,3 000,0)(单位:m),初始弹道倾角θm1=-10°,初始弹道偏角ψvm=-4°;目标初始位置(xt,yt,zt)为(20 000,5,1 000)(单位:m),以600m/s的速度匀速平飞,侧向加速度azt=100cos(0.5t)m/s2.
将导弹视为一阶延迟环节,速度变化规律为vm=1 500cos(0.03t)m/s,依据导引指令信息解算模型,对设计的基于零化相对速度偏角的三维变结构末制导律(VVSG)与增广比例导引律(APNG)进行仿真,其中,增广比例导引律的指令见文献[2].仿真结果如图3~图7所示.
图3为导弹与目标空间相对运动轨迹,目标在侧向平面内作幅值为800m,周期为7 000m的蛇行机动;图4和图5为滑模面S1和S2随时间变化的曲线;图6为导弹在弹道坐标系的纵向过载ny随时间变化的曲线;图7为导弹在弹道坐标系的侧向过载nz随时间变化的曲线.

图3 导弹-目标相对运动
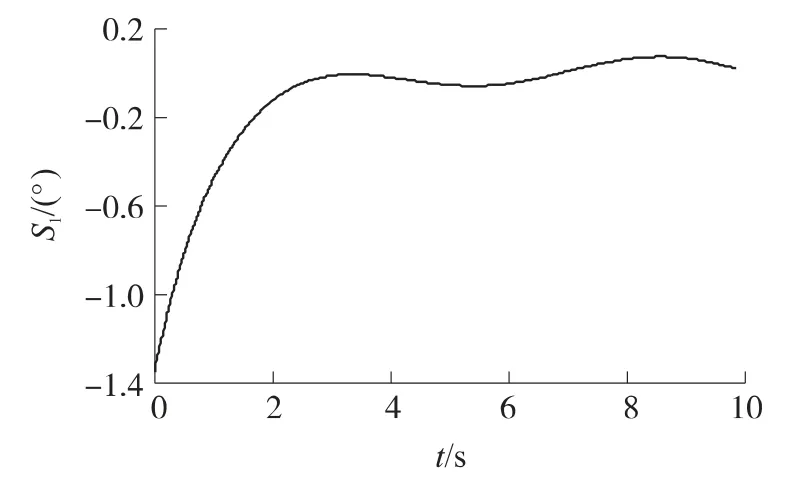
图4 滑模面S1变化曲线

图5 滑模面S2变化曲线

图6 导弹纵向过载ny变化曲线

图7 导弹侧向过载nz变化曲线
由图3可见,导弹弹道平滑,精确命中目标.由图4和图5可见滑模面S1和S2在制导初始时刻迅速趋于零,随着目标的机动,滑模面一直在零附近来回趋近,使得导弹与目标相对速度一直指向目标,确保精确命中目标.由图6和图7可见,采用所设计的基于零化相对速度偏角的空间变结构导引律,在减小末端需用过载方面优于增广比例导引律.
选取不同的视线角速度测量噪声均值,比较采用基于零化相对速度偏角的变结构导引律和增广比例导引律2种导引规律时导弹的飞行时间与脱靶量.仿真结果见表1,表中,E为噪声均值,t为导弹飞行时间,D为脱靶量.
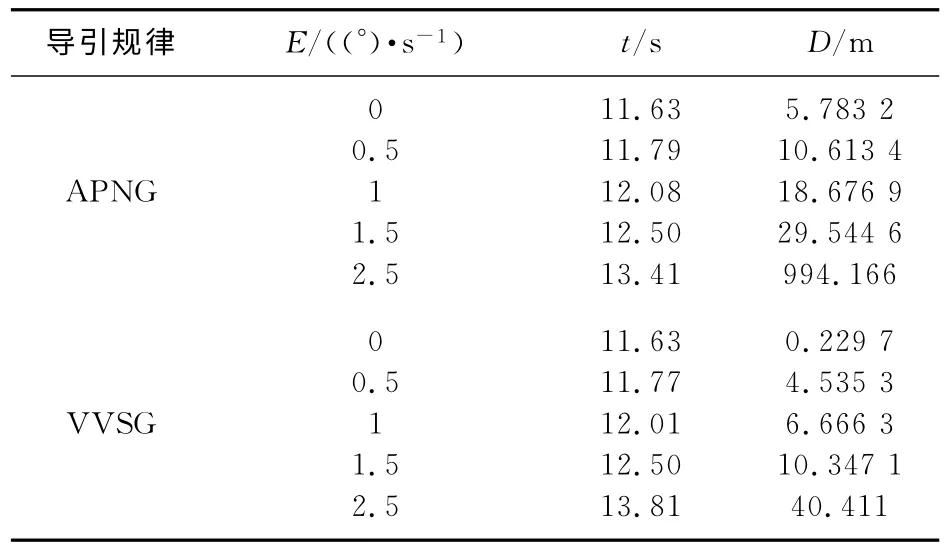
表1 视线角速度量测噪声对导弹飞行时间与脱靶量的影响结果
由表1的仿真结果可见,所设计基于零化相对速度偏角的变结构末制导律对视线角速度测量噪声较增广比例导引律具有更强的鲁棒性.
综上,图3至图7和表1的仿真结果不仅表明了所设计基于零化相对速度偏角的三维末制导律和指令信息解算模型的正确性,还验证了此末制导律对目标大机动和视线角速度测量噪声具有的强鲁棒性.
4 结束语
本文针对舰空导弹末端拦截掠海飞行目标问题,在空间选取导弹和目标的相对速度偏角作为零化目标,设计了一种基于零化相对速度偏角的三维变结构导引律,仿真结果验证了在对抗目标大机动和低空目标视线角速度量测噪声等方面,所设计导引律比传统的空间末制导律具有更强的鲁棒性,对基于零化相对速度偏角的导引算法设计思想在空间的推广具有一定的理论和借鉴价值.
[1]周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.ZHOU Di.Novel guidance law for homing missile[M].Beijing:National Defense Industry Press,2002.(in Chinese)
[2]张友安,胡云安.导弹控制和制导的非线性设计方法[M].北京:国防工业出版社,2003:154-162.ZHANG You-an,HU Yun-an.Nonlinear design approaches for missile control and guidance[M].Beijing:National Defense Industry Press,2003:154-162.(in Chinese)
[3]BYUNG S K,JANG G L,HYUNG S H.Biased PNG law for impact with angular constraint[J].IEEE Transactions on Aerospace and Electronic Systems,1998,34(1):277-288.
[4]TAL S.Optimal cooperative pursuit and evasion strategies against a homing missile[J].Journal of Guidance,Control and Dynamics,2011,34(2):414-425.
[5]宋建梅,张天桥.带末端落角约束的变结构导引律[J].弹道学报,2001,13(1):16-20.SONG Jian-mei,ZHANG Tian-qiao.The passive homing missile’s variable structure proportional navigation with terminal impact angular constraint[J].Journal of Ballistics,2001,13(1):16-20.(in Chinese)
[6]YU Xing-huo,MAN Zhi-hong.Fast terminal sliding mode control design for nonlinear dynamical systems[J].IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2004,49(2):261-265.
[7]TAL S,MOSHE I,ODED M G.Sliding mode control for integrated missile autopilot-guidance[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.Providence,Rhode Island:AIAA,2004:1-18.
[8]JONGKI M,KISEOK K,YOUDAN K.Design of missile guidance law via variable structure control[J].Journal of Guidance,Control and Dynamics,2001,24(4):659-664.
[9]张友安,胡云安,苏身榜.一种基于变结构控制的鲁棒制导算法设计[J].系统工程与电子技术,2001,23(4):61-63.ZHANG You-an,HU Yun-an,SU Shen-bang.A robust guidance algorithm design using variable structure control[J].Systems Engineering and Electronics,2001,23(4):61-63.(in Chinese)
[10]郭鸿武,林维菘,刘明俊.基于相对速度偏角的变结构导引律[J].宇航学报,2001,22(3):33-37.GUO Hong-wu,LIN Wei-song,LIU Ming-jun.A variable structure guidance law based on relative velocity deflection angle[J].Journal of Astronautics,2001,22(3):33-37.(in Chinese)
[11]林嘉新,赵永涛,胡云安.一种基于零化相对速度偏角的变结构末制导律设计[J].海军航空工程学院学报,2009,24(6):646-650.LIN Jia-xin,ZHAO yong-tao,HU Yun-an.Design of a variable structure terminal guidance law based on relative velocity deflection angle[J].Journal of Naval Aeronautical and Astronautical University,2009,24(6):646-650.(in Chinese)

