变结构空间飞行器发射过程的姿态研究
刘 赟,王 浩,季晓松,孙继兵
(1.南京理工大学 能源与动力工程学院,南京210094;2.南京炮兵学院,南京211132)
飞行器按照期望完成指定的飞行任务,如定向飞行、空间对接、打击目标等,都需要飞行器具有稳定及合理的姿态.为了保证飞行器的正常工作,研究人员对飞行器的姿态控制非常重视并进行了大量的研究.PEREIRA等[1]提出并验证了一种能够估计飞行器绝对姿态的简单算法,JING等[2]针对一类天文观测卫星的姿态控制率进行了研究,邵晓巍等[3]针对高超飞行器的特点建立了稳定有效的控制方案,乔洋等[4]提出了某小型再入航天器的初制导律.而某些飞行器并不具有姿态控制系统,或者姿态控制系统未能工作,对这类飞行器的研究有利于针对工作中出现的可能运动状态,提出相应的应对方案.随着空间技术的飞速发展,空间飞行器的结构日益复杂[5],经常要做大位移的运动,肖宁聪等[6]对卫星太阳翼的展开机构运动进行了可靠性研究,张华等[7]对空间飞行器的对接分离过程进行了地面模拟实验仿真研究,戈新生等[8]建立了自然坐标系下的空间机械臂动力学研究模型.这类空间飞行器的结构变化对姿态稳定是一种巨大考验.本文将研究一类由空间站释放的变结构空间飞行器在无控发射过程中的姿态变化.
该变结构飞行器包含动力装置、展开机构及防护罩三部分,主体结构如图1(a)所示.动力装置由释放火箭发动机和旋转火箭发动机及其连接件组成,展开机构包括伸缩杆、径向杆及支撑座等,防护罩则为圆锥形薄壳,与动力装置连接,包覆在展开机构外部.未展开前展开机构在轴向和径向都处于折叠状态,在头部动力装置作用下,展开机构轴向展开到位,触发径向展开条件,尾部的径向杆展开到位后,飞行器动力装置二次工作令其自旋,自此飞行器进入自由飞行阶段.在整个发射过程中飞行器经历2次结构变化,分别如图1(b)、图1(c)所示.飞行器发射过程姿态的变化对其之后的工作起着至关重要的作用,不良姿态将导致飞行器在自由飞行阶段不能正常工作,因此研究飞行器展开姿态有利于对飞行器自由飞行阶段的预测和分析.

图1 变结构飞行器结构变化
1 变结构飞行器数学模型
采用多体系统动力学方法对变结构飞行器进行数学建模.基本假设:飞行器各部件为刚体,部件理想加工装配,不考虑空气动力影响.
①发射惯性坐标系[9]O-xyz.在飞行器发射时支撑座质心所在位置建立发射惯性坐标系,如图2所示,Ox轴沿飞行器轴线方向指向头部为正,Oz轴指向地心为正,Oy轴与前两轴构成右旋正交系.
②空间飞行器部件固联系Oi-xiyizi.各部件的连体坐标系,原点固连于部件质心,坐标轴沿几何体的惯性主轴方向.以支撑座为例进行说明,原点固连在飞行器支撑座质心位置,初始时刻与发射惯性坐标系重合,坐标系随支撑座同时运动,文中没有特别说明均指在飞行器部件固联系下.

图2 飞行器坐标系
1.1 各部件运动模型
以一对相邻部件为单元,一个部件为参考物,另一部件的运动可由该部件的运动及单元间的相对运动等进行描述,采用规则标号法根据文献[10]建立各刚体部件质心关于发射惯性坐标系的一般运动模型:

式中,riii分别为刚体质心相对发射惯性坐标系的矢径、速度和加速度;下标i,k,l为部件编号为广义通路矢量,h1为支撑座移动矢径;ωkk为刚体相对发射惯性系的角速度及角加速度;ωL(l)为第l刚体的内接刚体相对发射惯性系的角速度;Tli为描述物体拓扑结构的参数,具体表达式详见文献[10];υrl,rl分别为连接铰Hl相对内接部件参考系的相对速度和相对加速度.
1.2 飞行器动力学模型
1.2.1 各部件动力学模型

式中,Δ为部件i的虚速度;ρiii分别为部件质心关于系统质心的矢径、速度和加速度;mi为部件质量;ms为系统总质量;下标j为部件编号;δij为克罗内克符号;Fi为作用于部件i质心的外力主矢;Δωi为部件i的虚角速度变化量;Ji为部件i关于质心的惯量张量;Mi为系统外力作用于部件i质心的主矩;ΔP为部件间相互作用的内力和各部件非理想约束力对系统任意虚速度所作的元功率之和.
1.2.2 发动机推力及力矩
发动机推力Ft存在偏角α和β.α为初始时刻推力在发射惯性系Oxz平面内的投影与Ox轴的夹角,规定在Ox轴上方为正;β为推力在Oxy平面内投影与Ox轴的夹角,规定沿Ox正向观测,在Ox轴左侧为正.则有推力Ft的坐标阵表达式:

式中,Ftx,Fty,Ftz分别为推力在3个坐标轴下的分量.
推力力矩Mt的坐标阵表达式:

式中,Mtx,Mty,Mtz分别为推力力矩在3个坐标轴下的分量;lx,ly,lz分别为推力作用点在释放火箭发动机连体基上的坐标分量.同理可建立旋转火箭发动机的推力及力矩模型.
1.2.3 重力梯度
在空间飞行器轨道上,重力本身非常小,因而轨道运动的离心力与重力相平衡,使飞行器成为失重状态,这就使哪怕很小的一点力矩的作用都会造成明显影响.因此,建立飞行器的重力梯度力矩Mg的坐标阵表达式[11]:


图3 飞行器发射过程时序工作流程
式中:μ为地球引力常量;R为飞行器系统质心距地心距离;Jx,Jy,Jz分别为飞行器绕3个惯性主轴的转动惯量;Jxy,Jxz,Jyz为惯性积;φ,θ分别为飞行器的滚转角和俯仰角.
飞行器几何对称,质量分布均匀,在系统质心上沿惯性主轴建立固连系,则方程中的刚体惯性积为零,式(7)化简为
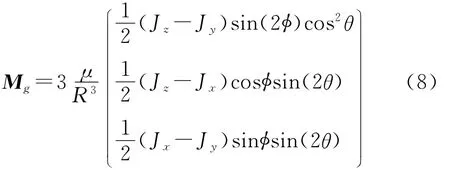
2 数值计算结果与分析
假设空间站位于1 000km太空轨道,飞行器沿发射惯性系Ox轴方向发射,释放火箭发动机产生推力范围为0~1 000N,稳定工作推力为320N,旋转火箭发动机产生扭矩范围为0~10.4N·m,稳定工作扭矩为8.75N·m.变结构空间飞行器发射过程从释放火箭发动机工作开始计算,至旋转火箭发动机工作结束,充分考虑了动力装置的时序工作误差,定义0.8s为飞行器的发射时长.飞行器发射过程的时间流程如图3所示.
2.1 飞行器理想发射运动研究
不考虑发射过程中的各种扰动,发射倾角为0°.图4和图5是理想发射情况下飞行器的运动变化曲线.图4中,x为展开机构轴向展开位移.为了表现小范围内飞行器的运动变化情况,图4进行了曲线截断处理,截断部分的曲线与截断前后曲线的变化状态一致.从图4可以看出,伸缩杆4在动力装置带动下开始沿轴向即沿Ox正向运动,依次带动轴向杆3和杆2运动,0.094s飞行器展开机构轴向展开到位,即完成第一次结构变化,图中0.094~0.1s之间曲线处于平台段,说明4根轴向杆保持展开形态不变.
图5中的δ为径向杆角位移,ω为飞行器的自转角速度.如图所示,0.097s径向杆开始运动,快速径向展开到位并保持不变,此时飞行器完成了第2次结构变化,图中0.12s附近的波动是径向杆的2次反弹,试验证明这种现象是存在的;0.1s时,飞行器与发射装置解除约束,所以图4中4根杆沿Ox轴同时运动,且速率相同.图6的姿态角,即滚转角φ,俯仰角θ,偏航角ψ,全部为零,说明飞行器仅沿x方向直线飞行,0.4s时旋转火箭发动机工作,飞行器开始自转,图6的滚转角开始增大;飞行器转速从0增加到1 280(°)/s并保持不变,如图5所示.
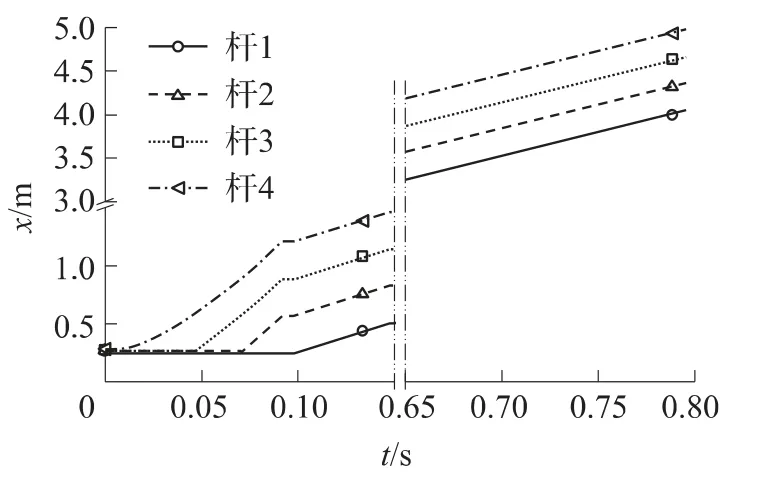
图4 展开机构轴向展开位移
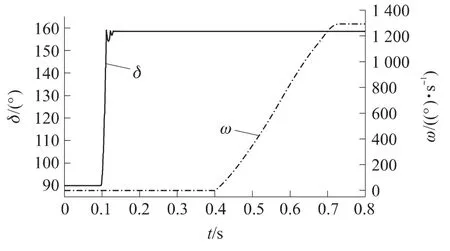
图5 径向杆角位移和飞行器角速度曲线

图6 飞行器姿态角随时间历程
对变结构飞行器进行了地面展开发射验证试验,虽然地面试验有大气的参与,但是在极短的发射时间内,飞行器受到发动机推力及自身结构剧烈变化的作用远大于空气动力对其产生的影响,因此试验结果是有效的.表1为试验结果与计算结果的部分参数对比,表中,ta为轴向杆拉开时间,tr为径向杆展开时间,td为旋转火箭发动机延迟时间,tc为飞行器接触约束时间.结果显示该变结构飞行器的多体系统动态求解模型能够很好地预测飞行器的运动过程.

表1 飞行器部分运动参数计算结果与试验结果的对比
2.2 推力偏心发射过程姿态
实际发射不能保证飞行器是绝对的理想状态,只能尽可能减小对发射产生不利影响的可能性.头部的动力装置由于装配及加工等因素的影响,产生的发动机推力不可能与Ox轴完全重合,因此采用相同发射动力下的飞行器理想发射模型,取沿Ox轴正向的释放火箭发动机推力偏向Oy轴正向1°,2°和3°,发射倾角0°.3种状态下飞行器的滚转角和俯仰角同图6,偏航角变化如图7所示.

图7 偏航角随时间历程
滚转角完全重合并且与理想状态一致,说明推力偏心对飞行器绕自身轴线的自转运动是没有明显影响的;释放火箭发动机的工作时间为0.21s,在飞行器自旋之前停止工作,因此飞行器推力偏心不会随着自转而在Oz轴产生分量,这是俯仰角变化为零的原因;偏航角在0.1s前保持零值不变,0.1s飞行器解除与发射装置的约束后,受到发动机推力在Oy轴正向产生的分力,该分力使得飞行器运动轨迹在发射惯性坐标系的xOy平面沿Oz轴发生偏移,即产生偏航角.当0.21s发动机停止工作后,飞行器将保持之前的运动趋势继续运动,偏航角随时间逐渐增大,并且随推力偏心角度的增加而增大.发射结束时3种状态中最小的1°推力偏心造成了23.8°的偏航角,飞行器已经产生了明显的沿Oz轴的翻滚,这对飞行器将来的稳定运动是非常不利的.由于采用无重力梯度模型,且飞行器为几何、质量分布均匀对称的轴对称系统,推力偏心偏向Ox轴和Oy轴具有相似性,偏向Ox轴将会造成俯仰角增大,偏向Oy轴则导致偏航角增大.
2.3 扭矩偏转发射过程姿态
采用相同发射动力下的飞行器理想发射模型,取沿Ox轴正向的旋转火箭发动机扭矩方向偏向Oy轴正向1°,2°和3°,发射倾角0°,得到的飞行器俯仰角和偏航角变化如图8所示,滚转角变化同图6.

图8 扭矩偏转下姿态角随时间历程
3种状态下的滚转角重合并且与理想状态一致,俯仰角和偏航角在0.4s即旋转火箭发动机开始工作后有变化.俯仰角随时间逐渐增大,并且在发射结束时有下降的趋势,偏航角先增大后减小.该阶段飞行器做类似陀螺运动,即存在与飞行器轴线有一定夹角的旋转轴.飞行器绕自身轴线自转的同时绕该轴旋转,从图中可以看出扭矩偏转同时影响俯仰角和偏航角,这是由于偏转角在发射坐标系下随飞行器的转动而变化,在Oy轴和Oz轴都有分量,使得飞行器的俯仰角和偏航角都改变,并且扭矩偏转角越大,改变越大.
2.4 重力梯度力矩对发射过程姿态的影响
采用相同发射动力下考虑重力梯度力矩的飞行器发射模型.为了更好地描述重力梯度力矩对飞行器姿态运动的影响,将飞行器沿发射惯性坐标系Oz轴正向偏转1°,2°和3°进行数值计算,即飞行器存在1°,2°和3°的发射倾角,得到飞行器的滚转角和偏航角变化同图6,俯仰角变化如图9所示.
3种状态下的滚转角和偏航角重合并且与理想状态一致,俯仰角保持初始发射角,无明显变化.因此,在发射过程中,小角度的发射倾角对飞行器发射阶段姿态的影响是可以忽略的.但是之后的自由飞行阶段,飞行器将一直受到重力梯度力矩的作用.飞行器在受到复杂空间力矩的作用下,将会改变飞行状态,其正常运动受到严重影响,这甚至会危及到控制系统的有效工作[12].因此重力梯度力矩对飞行器长时间工作的影响还需要进一步研究.
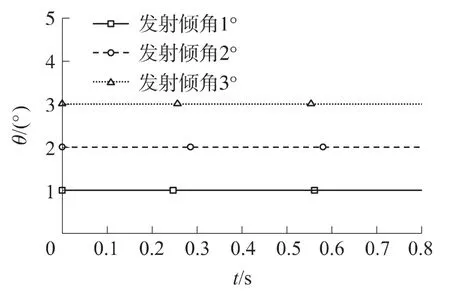
图9 俯仰角随时间历程
3 结论
①本文基于多体系统动力学方法,建立了变结构飞行器的动态研究模型,采用无干扰模型的数值计算结果与试验结果对比分析,该方法可以准确描述飞行器的运动历程.
②采用干扰模型分别对飞行器考虑推力偏心、扭矩偏转及重力梯度力矩3种情况进行了数值研究.数值计算结果表明:文中所研究飞行器的滚转角在3种小角度干扰情况下没有明显变化;推力偏心和扭矩偏转会造成飞行器偏离初始姿态,严重时可能产生沿非自旋轴的翻滚,扭矩偏转同时影响俯仰角和滚转角;重力梯度力矩对飞行器姿态角的影响在短时间小发射倾角范围内可以忽略.
③文中发射阶段姿态的研究为飞行器自由飞行阶段的姿态发展提供了研究基础,确立了初始条件,同时也为姿态控制研究人员提供相应参考.
[1]PEREIRA G A S,ISCOLD P,TORRES L A B.Airplane attitude estimation using computer vision:simple method and actual experiments[J].Electronics Letters,2008,44(22):1 303-1 305.
[2]JING W X,XIA X W,GAO C S,et al.Attitude control for spacecraft with swinging large-scale payload[J].Chinese Journal of Aeronautics,2011,24(3):309-317.
[3]邵晓巍,张军,牛云涛.高超飞行器的非线性预测姿态控制[J].弹道学报,2009,21(4):42-46.SHAO Xiao-wei,ZHANG Jun,NIU Yun-tao.Nonlinear redictive attitude control of hypersonic vehicle[J].Journal of Ballistics,2009,21(4):42-46.(in Chinese)
[4]乔洋,陈刚,徐敏,等.机动再入飞行器神经网络闭路初制导研究[J].弹道学报,2007,19(2):1-4.QIAO Yang,CHEN Gang,XU Min,et al.Initial guidance law of closed-from neural network for maneuverable reentry vehicle[J].Journal of Ballistics,2007,19(2):1-4.(in Chinese)
[5]赵艳彬,王萍萍,王本利,等.挠性飞行器姿态稳定鲁棒变结构控制[J].动力学与控制学报,2005,3(3):1-6.ZHAO Yan-bing,WANG Ping-ping,WANG Ben-li,et al.Application of variable structure robust attitude controller to flexible spacecraft[J].Journal of Dynamics and Control,2005,3(3):1-6.(in Chinese)
[6]肖宁聪.卫星太阳翼展开机构的可靠性分析方法研究[J].宇航学报,2009,30(4):1 704-1 710.XIAO Ning-cong.Reliability analysis method of deployment mechanism of a satellite solar arrays[J].Journal of Astronautics,2009,30(4):1 704-1 710.(in Chinese)
[7]张华,肖余之.空间飞行器的对接分离与地面模拟实验的仿真分析研究[J].宇航学报,2008,29(6):1 761-1 765.ZHANG Hua,XIAO Yu-zhi.Analysis study on separation of aerospace vehicle and ground simulation test[J].Journal of As-tronautics,2008,29(6):1 761-1 765.(in Chinese)
[8]戈新生,刘延柱.基于自然坐标的自由浮动空间机械臂动力学分析[J].力学与实践,2001,23(3):39-42.GE Xin-sheng,LIU Yan-zhu.On synamics analysis of space manipulator based on the fully cartesian coordinates[J].Mechanics in Engineering,2001,23(3):39-42.(in Chinese)
[9]胡小平,吴美平,王海丽,等.导弹飞行力学基础[M].长沙:国防科技大学出版社,2006.HU Xiao-ping,WU Mei-ping,WANG Hai-li,et al.The basics of missile flight mechanics[M].Changsha:National University of Defence Technology Press,2006.(in Chinese)
[10]洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,1999.HONG Jia-zhen.Computational dynamics of multibody systems[M].Beijing:Higher Education Press,1999.(in Chinese)
[11]刘暾,赵钧.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社,2003.LIU Tun,ZHAO Jun.Spacecraft dynamics[M].Harbin:Harbin Institute of Technology Press,2003.(in Chinese)
[12]隋起胜,袁建平,姜宇.重力梯度力矩引起的自旋稳定卫星姿态摄动[J].飞行器测控学报,2010,30(5):1-5.SUI Qi-sheng,YUAN Jian-ping,JIANG Yu.Attitude perturbation of spin-stabilized satellites caused by gravity gradient moment[J].Journal of Spacecraft TT & C Technology,2010,30(5):1-5.(in Chinese)

