多约束条件下导弹协同作战制导律
王晓芳,林 海
(北京理工大学 宇航学院,北京100081)
导弹防御系统的不断发展使导弹的突防能力和攻击能力面临着严峻的挑战.多导弹协同作战能够有效地提高导弹的突防能力、战场生存能力和对目标的打击能力.而多弹协同作战制导律是导弹实现协同作战的关键技术之一,对它的研究具有重要意义.
在导弹协同作战的过程中,通常对多枚导弹攻击目标时的攻击角度和攻击时间进行约束.对于具有攻击角度约束的制导律,国内外研究得比较多[1~3],而对于具有攻击时间约束的制导律的研究相对较少[4,5].近年来,学者们对于同时具有攻击角度和攻击时间约束的制导律也进行了一定的研究[6~8].文献[6,7]分别基于最优控制理论、滑膜控制理论提出了可同时控制多枚导弹攻击角度和攻击时间的制导律,文献[8]则采用反演控制方法和偏置比例导引法设计了一种具有攻击角度和时间约束的、适用于反舰导弹攻击固定目标的制导律,但文中并没有对制导律参数的取值进行研究.另外,在设计适用于导弹协同作战的制导律时,除了考虑攻击角度和攻击时间的约束,还需要考虑其他约束,如导弹自身的过载约束、弹道收敛性约束等.
本文在综合考虑攻击角度和攻击时间约束、导弹自身过载约束、弹道收敛性约束等因素的前提下,基于比例导引律设计了适用于多枚导弹协同作战的四维制导律,并采用自动控制理论和变系数比例导引律理论对制导律中参数的取值进行了理论分析,并给出了仿真算例.
1 具有攻击角度和攻击时间约束的制导律
某导弹和目标在三维空间的相对运动关系如图1所示.

图1 导弹目标相对运动图
图中:M代表导弹,M′代表导弹在水平面的投影,T代表目标;AXYZ为地面坐标系;MXMYMZM,M′XM′YM′ZM′,TXTYTZT为地面坐标系的平移坐标系,原点分别为M,M′,T;vM,θM,ψVM分别为导弹的速度、弹道倾角和弹道偏角;vT,θT,ψVT分别为目标的速度、竖直航向角和水平航向角;R为弹目距离;qy和qz分别为俯仰和偏航方向的视线角;q*y和q*z分别为俯仰和偏航方向的理想攻击角.假设导弹的速度大小不变,ay和az分别为导弹俯仰和偏航方向垂直于速度的加速度,则其运动模型为

式中,xM,yM,zM分别为导弹质心在地面坐标系中的坐标,g为重力加速度.为了实现对攻击角度和攻击时间的控制,可在纯比例导引律的基础上附加一个与角度差(实际视线角与理想攻击角之差)成正比的偏置量和一个与时间差(预估的攻击时间与理想攻击时间之差)成正比的偏置量,形成同时具有攻击角度和攻击时间约束的四维制导律,即

式中,Ky,at,Kz,at,Ny,a,Nz,a,Ny,t和Nz,t为 比 例 系数;t*为设定的理想攻击时间;t′为预估的攻击时间,它等于当前时刻t与导弹剩余飞行时间tgo(可通过任一种剩余飞行时间估算方法求得)之和.当qy和qz逐渐趋近于q*y和q*z,且t′逐渐趋近于t*时,此制导律逐渐变为纯比例导引律.在如式(2)所示的制导律中,系数Ky,at,Ny,a,Ny,t等的取值至关重要,它们直接关系到制导律的精度和导弹的弹道特性,需要综合考虑攻击角度和攻击时间约束、导弹的可用过载约束、弹道的收敛性约束等多个因素来取值.
2 多约束条件下制导律参数的选取
多枚导弹协同作战攻击的目标通常是具有强防御火力的高价值固定或慢速移动目标,因此,不失一般性,可假定目标为固定目标.为了研究同时具有攻击角度和攻击时间约束的制导律系数的取值,先分析只具有攻击角度约束的制导律系数的取值,即在式(2)中,令Ny,t=Nz,t=0.以俯仰平面的制导律为例,描述导弹目标之间的视线角和导弹弹道倾角变化的方程为
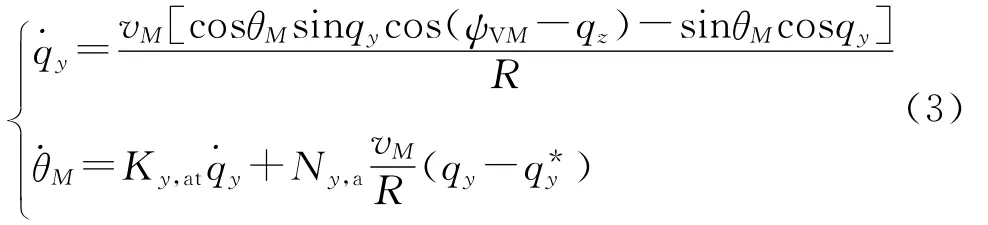
由于攻击的目标为固定目标,而且存在中制导,因此ψVM-qz不会太大,可认为cos(ψVM-qz)≈1,这时式(3)中的第一式变为
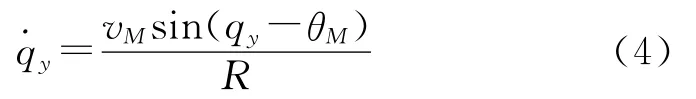
在qy-θM不大的前提下,有sin(qy-θM)≈qy-θM,再把近似后的y代入式(3)的第二式,则式(3)变为

由式(5)可看出,此时的导弹可看作q*y为输入、(qyθM)为状态变量的时变线性系统,如选qy作为输出,则可得到从q*y到qy的传递函数:
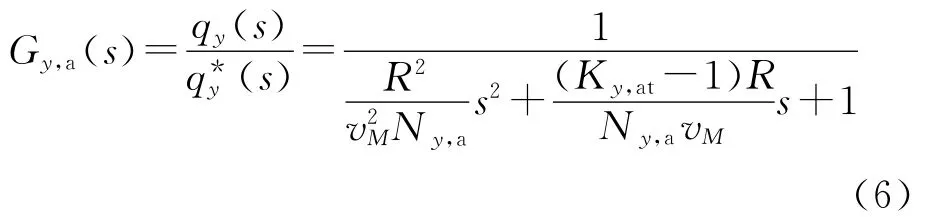
式中,s为复变量.由式(6)可知,它为一个传递系数kMy=1,时间常数,阻尼系数ξMy=
的二阶系统.如果系统稳定,qy将趋近于q*y.采用霍尔维茨判据来判断系统的稳定性,知系统稳定的充要条件为且,即

接下来分析制导律中的比例系数对系统动态特性的影响.从阻尼系数的表达式可知:当Ky,at确定后,阻尼系数只与Ny,a有关,Ny,a越大,阻尼系数越小;反之则阻尼系数越大.另外,由于导弹的速度vM不变,因此当弹目距离R一定时,系统的时间常数随着Ny,a的增大而减小.由此可见,Ny,a的取值对系统的动态特性有重要的影响.当要求导弹以某一角度命中目标即为常数时,相当于给式(6)所示的系统施加了一个阶跃输入.综合考虑过渡过程时间和超调量,根据自动控制理论可知,阻尼系数选在0.7左右,即0.5到1.0范围内时系统的过渡过程比较快,而且超调量也不大[9].因此可设定理想的阻尼系数<1.0),然后确定:

对于式(2)所示的同时具有攻击角度和攻击时间约束的制导律,类似于具有攻击角度约束的制导律的分析.经过简化和整理,描述视线角和导弹弹道倾角变化的方程为

根据式(9)求出以为输入、qy为输出的传递函数:

对比式(10)和式(6)可以发现:它们均是一个二阶系统,而且时间常数和阻尼系数的表达式也相同,不同的地方在于传递系数,式(10)中的传递系数包含了与攻击时间差有关的项.当t′→t*时,传递系数趋近于1.qy的变化不仅与时间常数、阻尼系数有关,还与攻击时间的控制项有关.如果t′越快地趋于t*,则Gy,at(s)越快地趋近于Gy,a(s),此时qy对的响应主要取决于时间常数和阻尼系数.由式(10)可知,此时系统的稳定条件同式(7),Ny,a仍然可按照式(8)来取值.
导弹在飞行过程中要受到自身可用过载的约束,可根据过载的约束决定Ny,t的取值.需要说明的是:当t′>t*时,导弹预估的飞行时间大于理想飞行时间,此时很难控制导弹以理想飞行时间命中目标,这时令Ny,t=0;当t′<t*时,偏置量起作用.以下分析当t′<t*时Ny,t的取值情况.将具有攻击角度和攻击时间约束的制导律式(2)的第一式代入式(1)的第二式后可得:


当t′<t*即导弹预估的飞行时间小于理想飞行时间时,根据比例导引律的特点,应有 ΔKy,t<0(Ny,t和y同号),使等效比例系数减小、导弹弹道抬高、导弹的飞行时间变长,以逐渐趋近于t*,实现对攻击时间的控制.在导弹协同作战初期,可充分发挥导弹的机动能力,以达到攻击时间和角度上的协同;在飞行弹道末段,则应使弹道收敛,以完成攻击目标这个主要任务.因此,在协同作战开始时,不妨设导弹达到了可用过载±ny,max(ny,max>0).则当y≥0时,n=-ny,max;y<0时,n=ny,max;即导弹的弹道形状与原弹道形状相反,以延长飞行时间.这时,在Ky,at和Ny,a已确定的前提下,可得:

式中:Ny,t0为导弹达到可用过载时Ny,t的临界值;y,qy,R,t′为初始时刻的值.协同作战开始时,导弹达到可用过载或以可用过载飞行一段时间,这时Ny,t的取值为

式中,k为系数.
为了确保导弹能够命中目标,在飞行弹道后段(命中目标前Δtl时间段内),要求弹道收敛.既然如式(2)所示的制导律可看作比例系数为K*y,at的变系数比例导引律,则可效仿传统比例导引律弹道收敛性的分析来研究它的收敛性.对式(3)的第一式求导,并整理可得:
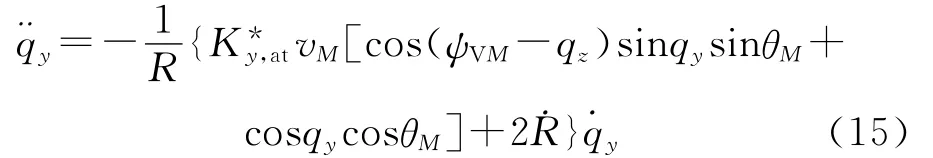
则弹道收敛的条件为
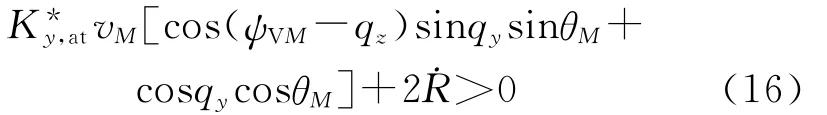
当ψVM-qz较小时,式(16)方括号中的值约等于cos(qy-θM),而在弹道末段,通常有|qy-θM|<90°,因此方括号中的值通常大于零,那么保证弹道收敛的K*y,at的取值范围即为

则

为弹道收敛的临界等效比例系数.导弹协同作战过程中,对攻击时间的控制相对攻击角度的控制显得更重要一些.如果导弹能够做到同时命中目标,即使攻击角度和设定的攻击角度有些误差,对攻击效果的影响也不会太大.因此,在弹道末段,保持Ny,t不变,而根据弹道收敛的条件改变Ny,a.将K*y,at的表达式代入式(17),则得到在弹道收敛前提下的Ny,a的取值范围:
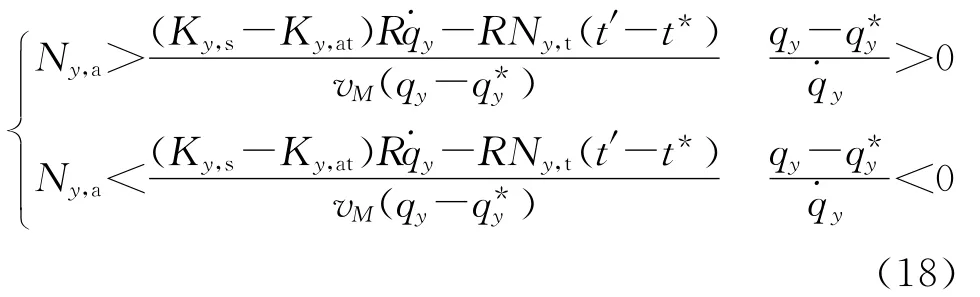
经过以上分析,综合考虑导弹的动态过程、可用过载的约束以及弹道收敛性等因素,可按照以下原则选取制导律中的系数:
①根据经验首先选取Ky,at∈[2,6].
②基于式(8)根据设定的理想阻尼系数ξM*y计算Ny,a.
③根据Ky,at和Ny,a,按照式(13)和式(14)设定弹道初始段导弹按可用过载飞行时的Ny,t.
④在导弹飞行末段,当tgo<Δtl时,保持Ky,a和Ny,t不变,如Ny,a满足不等式(18),则其保持不变;否则Ny,a由式(18)进行修正.当导弹攻击固定目标且弹道收敛时,导弹的需用过载会逐渐趋于零.
偏航方向制导律的分析类似于俯仰方向,受篇幅局限,在此不再叙述.
3 仿真结果及分析
假设3枚导弹采用爬升—平飞—俯冲弹道协同攻击敌军舰,导弹在平飞段对目标进行搜索,当其中一枚导弹发现目标后通知其他导弹,然后3枚导弹进入末制导,对目标进行协同攻击.通过考虑导引头的最大识别距离来设定导弹目标的初始位置.设军舰的位置为(8 775,0,2 000)(单位:m),3枚导弹的初始参数如表1所示.表中XM,YM,ZM分别表示导弹质心在地面坐标系中的坐标;nmax表示导弹在俯仰和偏航方向的可用过载.

表1 3枚导弹的初始参数
设3枚导弹的理想攻击角度()分别为(-35°,-50°)、(-45°,10°)和(-45°,70°),理想攻击时间t*=54s.对于俯仰方向的制导律,比例系数Ky,at=4,理想阻尼系数=0.8.Ny,t取如式(13)所示的临界值的k倍,此处k=5.末段弹道收敛时间Δtl=3s,当tgo<Δtl时,如弹道不收敛,保持Ky,at和Ny,t不 变,对Ny,a进 行 修 正.根 据式(18)知弹道收敛要求下Ny,a的临界取值为

Ny,a的修正方法为

为了在保证弹道收敛的前提下尽量对攻击角度进行较强的控制,修正时Ny,a取较Nly增大或减小10%的值,正如式(19)所示.偏航方向制导律中系数的取值方法同俯仰方向.仿真结果如图2和图3所示,图2中的q表示视线角,qyi和qzi(i=1,2,3)表示第i枚导弹俯仰和偏航方向的视线角.

图2 3枚导弹视线角变化曲线
由图2和图3可看出,3枚导弹以要求的攻击角几乎同时命中目标.需要说明的是,弹道末段的修正对攻击角度的控制有一定影响,但影响并不大.本算例中,在俯仰方向,3枚导弹的实际攻击角与理想攻击角之差最大为0.7°,修正前后的攻击角的最大差别不超过1°.偏航方向上,实际攻击角与理想攻击角之差最大为1.9°,修正前后攻击角的差别也不超过2°.攻击时间方面,3枚导弹的实际攻击时间与理想攻击时间的最大偏差为0.7s,3枚导弹的实际攻击时间最大偏差为1.4s.这些说明制导律具有良好的精度.以导弹1为例,画出其过载变化图和末段弹道修正前后的视线角速度变化图,如图4和图5所示.图中,n为过载,为视线角速度.

图3 3枚导弹弹道图
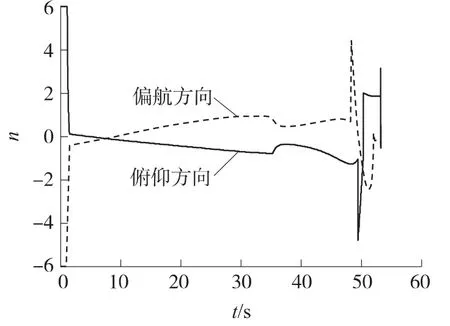
图4 导弹1的过载变化
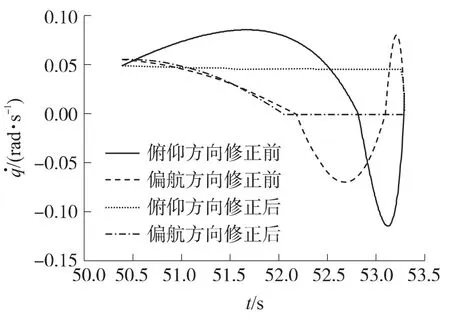
图5 末段修正前后导弹1的视线角速度变化曲线
由图4可知,导弹按可用过载飞行一段时间之后,需用过载就小于可用过载.在导弹飞行末段,过载发生突变是由于视线角速度的符号发生变化导致制导律中控制攻击时间的部分符号突变,过载因此发生突变.由图5可看出,根据弹道收敛性约束对制导律中的系数进行修正后,视线角速度逐渐收敛,有利于有效地攻击目标.
4 结束语
本文研究了多枚导弹协同作战时多约束条件下的制导律问题,所做工作具有以下特点:
①将与攻击角度和攻击时间约束有关的偏置量附加到纯比例导引律信号中,形成对导弹攻击角度和攻击时间进行控制的制导律.
②基于控制理论研究了保证导弹系统稳定和攻击角度响应具有良好动态特性的制导律参数的选择;基于变系数比例导引律理论,研究了保证末段弹道收敛的制导律系数;综合考虑导弹可用过载的约束,给出了制导律参数的取值方法.仿真算例验证了制导律的有效性.
需要说明的是,对于多导弹协同攻击慢速直线运动目标的情况,本文对制导律中系数取值的推导方法仍然适用.制导律中的理想攻击时间的取值比较关键,它与导弹目标的初始位置、导弹的可用过载、目标的运动状态等都有关系,因此,它的合理设定以及制导律的应用范围是下一步要研究的内容.
[1]OHLMEYER E J,PHILIPS C A.Generalized vector explicit guidance[J].Journal of Guidance,Control,and Dynamics,2006,29(2):261-268.
[2]RATNOO A,GHOSE D.State dependent riccati equation based guidance law for impact angle constrained trajectories[J].Journal of Guidance,Control,and Dynamics,2009,32(1):320-326.
[3]顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计[J].飞行力学,2006,24(2):43-46.GU Wen-jin,LEI Jun-wei,PAN Chang-peng.Design of the climbing trajectory using virtual target’s proportional navigation method with the control of terminal azimuth of a missile[J].Flight Dynamics,2006,24(2):43-46.(in Chinese)
[4]JEON I S,LEE J I,TAHK M J.Impact-time-control guidance law for anti-ship missiles[J].IEEE Transactions on Control Systems Technology,2006,14(2):260-266.
[5]张友安,马国欣,王兴平.多导弹时间协同制导:一种领弹-被领弹策略[J].航空学报,2009,30(6):1 109-1 118.ZHANG You-an,MA Guo-xin,WANG Xing-ping.Time-cooperative guidance for multi-missiles:a leader-follower strategy[J].Acta Aeronautica et Astronautica Sinica,2009,30(6):1 109-1 118.(in Chinese)
[6]LEE J I,JEON I S,TAHK M J.Guidance law to control impact time and angle[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):301-310.
[7]HARL N,BALAKRISHNAN S N.Impact time and angle guidance with sliding mode control[C].AIAA Guidance,Navigation,and Control Conference.Chicago,Illinois:AIAA,2009:1-22.
[8]JUNG B,KIM Y.Guidance laws for anti-ship missiles using impact angle and impact time[C].AIAA Guidance,Navigation,and Control Conference and Exhibit.Keystone,Colorado:AIAA,2006:1-13.
[9]吴麒.自动控制原理[M].北京:清华大学出版社,1998:138-139.WU Qi.Principles of automatic control[M].Beijing:Tsinghua University Press,1998:138-139.(in Chinese)

