侵彻制导武器BTT末制导奇异性控制策略
温求遒,李 然,何 镜
(1.北京理工大学 宇航学院,北京100081;2.中国兵器工业集团公司,北京100081)
现代战争中,对目标实施有效的远程精确打击已成为战争的首选方案.新一代空地制导武器,如美国的小直径炸弹(SDB)、联合防区外武器(JSOW),普遍采用非原截面升力体外形及可折叠弹翼,实现对目标的远程高精度打击;战斗部上采用大长径比侵彻战斗部,具备打击深层硬目标的能力[1].因此在控制上使用BTT(Bank-to-Turn)控制技术以保证导弹具有足够的机动能力,并消除气动耦合影响[2];同时使用以弹道成型制导律为代表的多约束最优制导律替代比例导引,满足侵彻战斗部对导弹高落点精度、大落角及落速的要求.
BTT控制技术在战术导弹中的应用主要集中在初中制导方案转弯或航路跟踪段,此时导弹飞行过程较平稳,制导指令变化小[3].而在末制导段,仍然存在着诸多问题,如何消除BTT控制奇异性是其中的一个关键问题.BTT控制奇异性是指在滚转控制指令转换过程中,俯仰、航向制导指令微小的变化带来滚转的剧烈震荡的现象,滚转角指令变化幅度甚至可达到±90°.一旦进入奇异性,滚转控制回路极易出现饱和,同时快速滚转会诱发大的气动与运动学耦合,严重影响到弹体稳定控制及制导精度[4].
奇异性问题的产生与导弹俯仰、偏航通道制导指令密切相关[4],这决定了必须根据回路中采用的制导律,总结其指令变化规律,并结合存在的计算不确定性与噪声,设计相应的控制策略,才能达到最优的效果.
本文针对空地侵彻制导武器BTT末制导奇异性控制问题,首先基于BTT-90指令转换逻辑,分析了奇异性产生的机理及主要影响因素;结合理论分析与弹道仿真计算,给出了制导回路指令特点及奇异性产生的原因;以此为基础,提出了包含控制区域划分及滚转指令平滑算法的奇异性控制策略;最后通过仿真证明控制策略的有效性.
1 BTT控制奇异性问题
1.1 BTT制导控制原理
BTT控制方式下制导控制系统工作原理框图如图1所示,根据惯性导航系统或导引头提供的弹目相对信息按照制导律生成惯性坐标系内的俯仰、偏航制导指令ayc,azc;经指令转换环节,计算俯仰控制指令aybc和滚转控制指令γc.在导弹转弯过程中,偏航驾驶仪侧向过载指令azbc取零,以保证零侧滑角,起到协调转弯的作用.
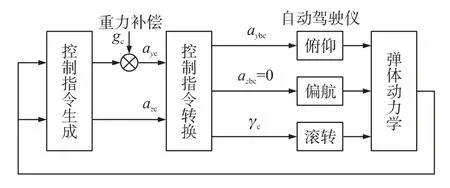
图1 BTT制导控制回路工作原理
在末导段,除最大过载外,侵彻制导武器对正负攻角通常没有限制;同时考虑空地导弹以俯仰平面为主要机动面,因此取滚转指令范围为±90°,并通过aybc符号正负变化实现在全平面的机动,又称为BTT-90逻辑,计算模型为

式中,sign为符号函数.
1.2 BTT制导奇异性分析
为计算γc对其自变量ayc,azc变化的敏感程度,分析奇异性产生的机理,引入偏导数的概念,其物理意义是表示函数关于自变量的变化快慢程度.由式(1)不难得到γc关于ayc,azc的偏导:
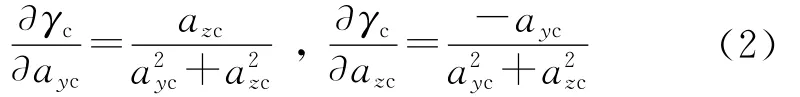
当ayc及azc取不同值时,∂γc/∂ayc,∂γc/∂azc变化曲线如图2~图3所示.不难得出如下变化规律:∂γc/∂ayc与ayc呈反比关系,ayc越小,∂γc/∂ayc越大;当ayc接近0时,∂γc/∂ayc达到最大,这表明γc对ayc在零附近的变化非常敏感.∂γc/∂azc的变化取决于ayc,azc的大小相对关系,当|ayc|>|azc|时,∂γc/∂azc随ayc增大而减小;而当|ayc|<|azc|时则反之;当|ayc|=|azc|时,∂γc/∂azc有最大值.这表明纵向指令ayc越小,γc对ayc变化敏感度越大;侧向指令azc越小,∂γc/∂ayc,max,∂γc/∂azc,max数值越大,即γc变化的幅度越大.

图2 ∂γc/∂ayc随ayc变化曲线

图3 ∂γc/∂azc随ayc变化曲线
图4给出了azc取不同值时滚转指令随ayc变化曲线.ayc越小,γc随着ayc变化越剧烈,特别在ayc过零前后,γc出现±90°跳变.
以上分析表明,在BTT-90逻辑中,俯仰指令ayc为小量,是导致BTT控制奇异性的主要原因,特别在过零附近,滚转指令的变化幅度最大.

图4 azc取不同值时,γc随ayc变化曲线
2 制导律指令变化规律分析
以侵彻制导炸弹为例,偏航制导回路主要是修正离轴投放带来的初始速度偏差并消除飞行过程中各种干扰,全程采用比例导引制导律.因此,如果在末端不出现大的干扰(如风切变),偏航指令azc非常小,近似为小量.
为满足侵彻所需的末端多约束条件,俯仰制导回路采用基于落角及落点约束的弹道成型制导律[4]:

式中,vr为弹目相对速度,为弹目视线角速度,q为弹目视线角,tgo为剩余飞行时间,qF为装订的期望落角值.为简化量纲,在本文的分析中角度均采用弧度单位.
为便于研究过载指令在制导过程中的变化规律,对于任意时刻t,式(3)可写为关于弹目初始相对位置y0、末端法向速度F、制导时间tF的表达形式[5]:

式(4)由以下3部分组成,其对应的物理意义如下.
由初始位置偏差引起的制导指令:

由初始法向速度引起的制导指令:

由末端法向速度约束引起的制导指令:
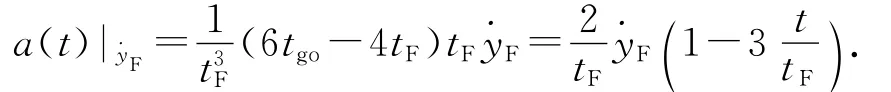
由于该制导问题是在初始弹目线系下进行研究的[6],所以一般情况下初始位置偏差y0=0,即a(t)|y0=0.而在小角度假设下,初始法向速度可用沿弹目视线方向上的相对接近速度vr与初始时刻速度指向误差角ε表示,即0=vrε;而终端法向速度可用vr与期望落角值qF表示,即F=vrqF.故以初始速度指向误差角ε和终端落角qF表述的制导指令变化规律为

为研究方便,取初始速度指向误差角ε和期望落角qF的关系k=ε/qF.显然相对角度比k在物理上反映了制导过程需要完成的角度修正,因而制导过程付出的制导指令大小与其密切相关.取无量纲时间=t/tF,代入式(5),得到无量纲过载表达式:

取空地武器典型投弹高度为4~10km,射程范围为10~40km,可得初始误差角ε取值范围为-10°~-40°;侵彻战斗部末端落角要求为不低于-60°,取落角值范围为-60°~-80°,不难计算得到k取值为0.1~0.8.
图5给出了k取不同值时对应的制导律无量纲过载曲线.弹道成型制导律过载指令随时间变化近似于线性递减的关系.初始时刻出现最大正过载,目的是使弹道上抬;之后逐渐减小,待过零后转为负过载下压,使弹道低头,从而获得较大落角;过载指令在命中点处达到负最大值.因此不同于比例导引末端过载指令逐渐收敛至零,弹道成型制导律在制导末端过载指令很大,且在多数制导时间内也均为大指令,小指令只存在于制导中段过零阶段附近短时间内.
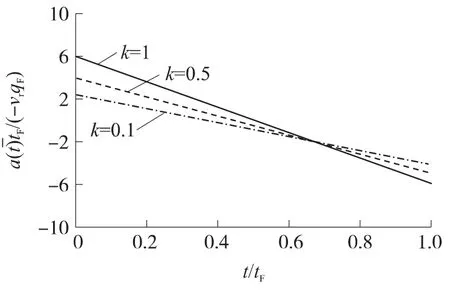
图5 不同k值对应的无量纲加速度曲线
在制导中,纵向重力补偿及控制回路动力学滞后都会影响指令变化,因此还需通过实际仿真计算证明理论分析结论.图6给出了H=6km投放,分别取装订落角值qF=-1.04rad,-1.22rad,-1.40rad(分别对应-60°,-70°,-80°),攻击R=20km目标时纵向弹道及过载指令仿真曲线,与理论分析的结果基本是一致的,只是过零段时间更接近制导末端.综合前文分析,对采用弹道成型制导律的BTT末制导,只需要在俯仰过载指令过零阶段采用奇异性控制.

图6 不同装订落角对应弹道及过载指令曲线
3 奇异性控制策略
3.1 控制区域划分与切换条件设计
根据制导段弹道特点与两通道指令变化规律,将BTT滚转角指令计算划分为正常控制区和奇异性控制区,在不同的区域选取对应计算策略.即在非奇异性区域采用标准BTT-90策略,在奇异性区域采用指令平滑算法以减小滚转角指令出现大幅跳变或震荡的情况.
由于俯仰指令ayc变化是诱发奇异性的主要原因,因此选择以此作为控制区域切换条件.定义ayc,0为切换量,当|ayc|<ayc,0时,由正常控制区切换至奇异性控制区.在实际飞行过程中,随机风、导引头信号噪声等干扰因素都会导致ayc存在计算噪声及一定的不确定性,这可通过引入阈值系数c,如图7所示,通过增加切换面厚度的方式防止在正常控制区和奇异控制区间误切换,即

式中,ayc,1=ayc,0+c.
ayc,0取值通常不能太大,以尽量减小对制导的影响;同时可根据azc值不同范围确定多个ayc,0值,azc值越小,相应的ayc,0取值越大.阈值系数c可通过对ayc噪声水平统计来确定.

图7 正常控制区与奇异控制区切换示意图
3.2 滚转指令平滑算法
由于弹道成型制导律下ayc在过零段符合线性单调递减规律,且过零段基本处于制导中末段,此时偏航指令azc基本为零,因此若假设在奇异性控制区进入切换点ayc,0,有滚转指令γc,0,则退出切换点ayc,1对应的滚转指令γc,1是可估计的,且有γc,1≈-γc,0.已知控制区两端的节点(ayc,0,γc,0),(ayc,1,γc,1),以ayc为变量,得到γc线性插值平滑计算函数:

式(7)中,对边界点滚转指令预估值γc,1的设计十分重要.γc,1值过大会使得奇异区内滚转角指令随ayc变化过于缓慢,虽能较好地消除BTT控制奇异性的影响,但会造成滚转角实际指令与期望指令之间的偏差较大,对退出到正常控制区后制导带来较大的影响;γc,1值过小会使得奇异区内的滚转角指令关于ayc的变化斜率过大,导致滚转角指令平滑变化程度不足.-γc,0只给出了一个近似参考值,实际设计时还需根据弹道仿真情况进行修正,以兼顾平滑效果与制导精度.滚转指令平滑计算示意图如图8所示.
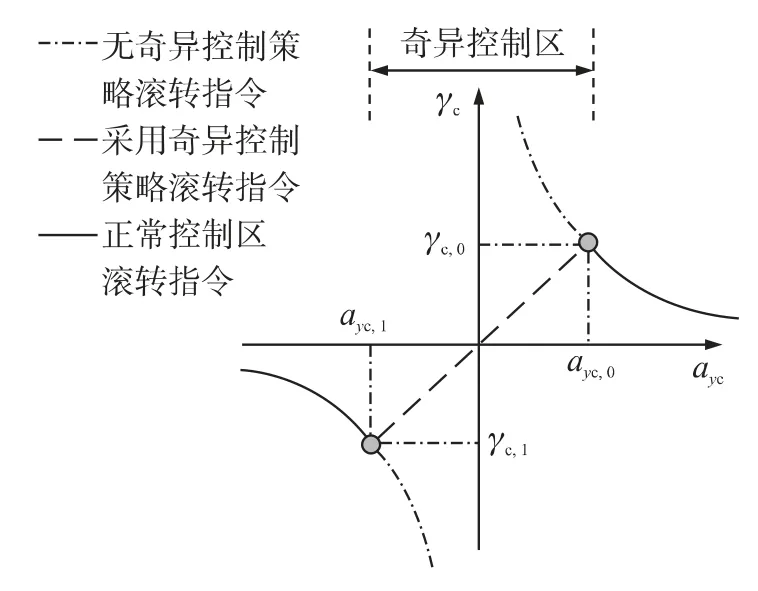
图8 滚转指令平滑计算示意图
在计算滚转指令的同时,俯仰指令依然保持原计算方法不变.
4 仿真结果
取投弹高度H=6km,射程R=30km,离轴发射角15°,采用包含随机干扰及导引头量测噪声的六自由度模型进行仿真[7].如图9所示,在干扰的作用下,俯仰及偏航过载指令中存在均方差σ=0.1g的噪声.

图9 纵、侧向过载指令
图10给出了有、无奇异性控制策略滚转角指令对比曲线,在正常控制区域内,两者是相同的.而在过零段,未采用奇异性控制时,滚转角指令剧烈震荡,滚转舵饱和,如图11所示;而采用奇异性控制有效消除了滚转角指令跳变现象,滚转舵资源消耗小,转出到正常控制后,滚转指令无大的变化,对末端制导影响小.

图10 有、无奇异性控制,滚转角指令对比曲线
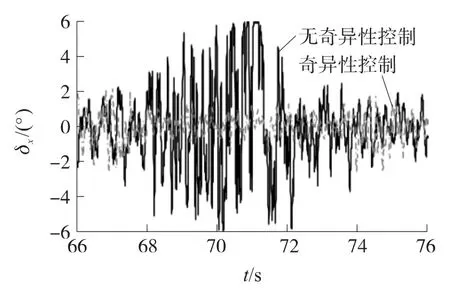
图11 有、无奇异性控制,滚转舵偏角对比曲线
5 结论
BTT控制方式下,根据惯性系下俯仰、偏航制导指令,采用反正切的方法计算所需的滚转控制指令,因此不可避免地出现计算的奇异性.通过基于偏导的灵敏度分析可知,两通道处于小指令是导致滚转指令计算奇异性的根本原因,且以俯仰指令影响程度最大.针对末制导采用的弹道成型制导律,推导了过载指令随制导时间变化解析表达式并进行了无量纲化.结合实际弹道仿真结果,证明了奇异性仅存在于过载指令过零阶段,且指令在过零段具有单调递减特性;以此为基础,提出一种将BTT控制划分为正常控制与奇异性区域,并在奇异性控制区采用滚转指令平滑算法的奇异性控制策略,给出了控制区切换条件,有效地抑制了奇异性的产生.
[1]石艳霞,郝丽萍.国外钻地武器的技术特点及发展趋势[J].导弹与航天运载技术,2003,264(4):50-53.SHI Yan-xia,HAO Li-ping.Characteristic and development of penatration weapon abroad[J].Missile and Space Vehicles,2003,264(4):50-53.(in Chinese)
[2]孙宝彩.巡航飞行导弹BTT自动驾驶仪设计方法研究[D].北京:北京理工大学,2007.SUN Bao-cai.Study of BTT autopilot design based on cruise missiles[D].Beijing:Beijing Institute of Technology,2007.(in Chinese)
[3]张友安,杨旭,崔平远,等.倾斜转弯飞航导弹的制导与控制问题研究[J].宇航学报,2000,21(4):71-75.ZHANG You-an,YANG Xu,CUI Ping-yuan,et al.Research of guidance and control for BTT winged missile[J].Journal of Astronautics,2000,21(4):71-75.(in Chinese)
[4]张飞宇.BTT导弹利亚普诺夫制导律的工程应用[J].弹道学报,2011,23(1):80-83.ZHANG Fei-yu.Engineering application of Lyapunov guidance law on bank-to-turn missile[J].Journal of Ballistics,2011,23(1):80-83.(in Chinese)
[5]ZARCHAN P.Tactical and strategic missile guidance[M].Washington D C:AIAA,2002.
[6]VINCENT C L.Circular guidance laws with and without terminal velocity direction constraints.AIAA 2008-7 304[R].2008.
[7]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2003:46-50.QIAN Xing-fang,LIN Rui-xiong,ZHAO Yan-an.Missile flight mechanics[M].Beijing:Beijing Institute of Technology Press,2003:46-50.(in Chinese)

