基于一种改进CA模型模拟双辊连续铸轧纯铝微观组织

陈守东，陈敬超，彭 平

(昆明理工大学，稀贵及有色金属先进材料教育部重点实验室，云南省新材料制备与加工重点实验室，昆明650093)

基于一种改进CA模型模拟双辊连续铸轧纯铝微观组织

陈守东，陈敬超，彭 平

(昆明理工大学，稀贵及有色金属先进材料教育部重点实验室，云南省新材料制备与加工重点实验室，昆明650093)

基于枝晶生长的基本传输过程和元胞自动机(Cellular Automaton，简称CA)-有限元(Finite Element，简称FE)模型基本原理，建立了适应双辊连续铸轧纯铝薄带工艺特点的凝固过程形核和晶体生长的数学模型.模型耦合了宏观温度场和微观组织模拟计算，考虑了溶质扩散、曲率过冷和各向异性等重要因素的影响，定义了界面单元捕获规则，能够模拟凝固过程中枝晶生长的形态.应用本模型对双辊连续铸轧纯铝薄带凝固过程中等轴晶生长、等轴晶多晶粒生长及柱状晶生长、柱状晶向等轴晶演化进行模拟并与实验结果进行对比，模拟结果与实验结果吻合较好，验证了模型的正确性.

纯铝;双辊连续铸轧;凝固微观组织模拟;元胞自动机-有限元方法;枝晶形貌

双辊薄带连铸技术是冶金及材料领域内的一项前沿技术，其特点为:简化生产工序，缩短生产周期，减少设备投资，降低生产成本等方面，具有巨大的技术和经济潜力.虽然国内外在双辊薄带连铸凝固过程的数值模拟方面已进行了大量的研究［1-5］，但对薄带凝固组织形成的微观模型研究还非常少，尤其是薄带凝固过程中枝晶生长模型的研究.

铸件微观组织决定着铸件的最终机械性能和力学性能［6］，对铸坯质量有重要影响，是冶金、材料、铸造企业关注和研究的重点问题.采用计算机仿真方法研究金属凝固组织的形成过程，可以快速预测金属凝固组织的形成以及工艺参数对凝固组织形成的影响，通过模拟计算可以分析微观组织界面形态、枝晶结构转变，能从理论上解释枝晶演化和微观组织形成的本质原因，预测铸轧工艺参数、物性参数和凝固参数对凝固组织的影响，从而对铸件性能改性提供理论基础［7-8］.在凝固微观组织模拟技术中，元胞自动机(CA)方法以过程的随机性为基础，结合了形核的物理机制和晶体生长动力学理论，同时具有随机性方法和确定性方法的共同优点，近年来应用广泛，发展较快.

在国外，Beltran-Sanchez和 Stefanescu［9-10］基于CA方法，建立了低Peclet数的二元合金中由溶质扩散控制的枝晶生长微观模型，该模型考虑了网格的局部曲率、凝固分数、捕获原则和各向异性等对枝晶生长形貌的影响，同时减小了网格划分对模拟结果的影响.Raghavan等［11］采用一种改进的CA模型模拟了包晶合金的凝固显微组织，提出了模拟包晶反应第二固相的形核和两个固相竞争生长的算法.在国内，李强等［12］采用CA方法对单个枝晶在凝固过程中的显微偏析和枝晶形貌进行了模拟，考虑了固/液两相的溶质传输问题.朱鸣芳等［13］应用一种改进的二维CA-传输耦合模型，对流场作用下的Al-3%Cu合金枝晶的非对称生长进行了模拟研究.Wang等［14］应用二维和三维CA模型对镍基高温合金的定向凝固过程进行了模拟，研究了枝晶生长速度的扰动对一次枝晶臂间距和枝晶尖端过冷的影响.但是，目前大规模多晶粒的三维微观组织模拟仍较少见，而针对双辊连续铸轧纯铝薄带凝固微观组织演化的模拟研究更是鲜有报道.

本文基于一种改进的CA方法及枝晶生长的基本传输过程，建立了双辊连续铸轧纯铝薄带凝固过程中枝晶形核生长的数学模型，该模型耦合了宏观温度场和微观溶质场计算，同时考虑了成分过冷、曲率过冷和各向异性等重要因素对枝晶形貌的影响.该模型能够模拟双辊连续铸轧纯铝薄带凝固过程中枝晶的复杂形貌.通过对双辊连续铸轧纯铝薄带凝固过程中等轴晶、等轴晶多晶粒以及柱状晶向等轴晶演变的模拟结果表明，本模型具有较好的理论和应用价值.

1 数理模型

1.1 宏观温度场模型

对双辊连续铸轧纯铝薄带凝固过程进行数值模拟的前提就是建立铸轧区、铸轧辊和环境之间的传热模型.根据双辊连续铸轧工艺的特点，计算主要是基于不稳定导热偏微分方程的基本数学模型［15］.

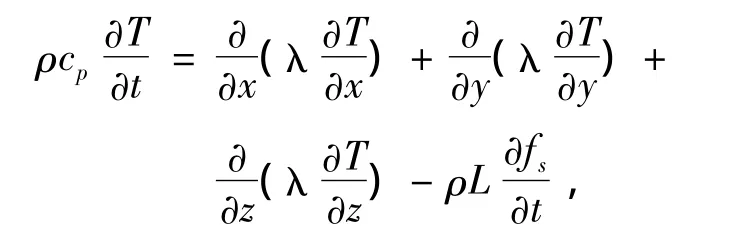
式中:ρ为合金密度;cp为定压比热容;T为温度;t为时间;λ为热导率;L为结晶潜热;fs为质量固相率;x，y，z分别为3个坐标轴方向上的坐标.

1.2 异质形核模型

针对双辊连续铸轧纯铝薄带的特点来说，通常在铸轧区的熔体中加入晶粒细化剂进行变质处理，其原理就是在铝熔体中加入Al-Ti-B丝材，反应生成大量弥散分布的高熔点TiAl3相和TiB2相，这样可以作为非均匀形核的质点，以达到细化晶粒的作用，本文采用Rappaz等［16-17］提出的基于高斯分布的连续性异质形核模型，在某一过冷度ΔT时所形成晶粒密度n(ΔT)可由该分布曲线的积分求得

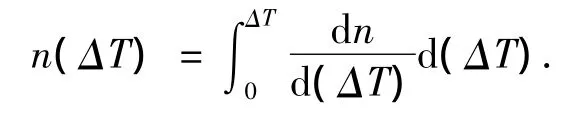
取高斯分布得

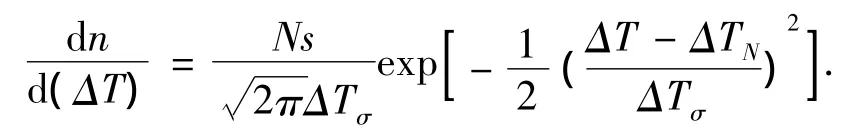
式中，fs为固相分数.鉴于双辊连续铸轧的工艺特点，对铸轧辊面和铸轧区内分别采用两种不同的形核分布函数，采用不同的形核密度.

1.3 枝晶尖端生长动力学模型

晶体的生长过程一般是通过采用枝晶尖端半径和生长速度两个因素来描述的.采用Kurz［18］和Rappaz等［19］描述枝晶尖端生长的动力学模型(KGT)，该模型考虑了溶质分配系数、扩散系数及相图参数的影响.

式中:n(ΔT)为过冷度ΔT时的晶核密度，ΔT=TL-T(TL为液相线温度);Ns为总的初始形核质点密度;ΔTN，ΔTσ为合金的最大形核过冷度和标准方差过冷度.

鉴于晶粒生长对形核位置的消减作用，形核密度n(ΔT)将变为

为能获得枝晶尖端生长速度v和枝晶尖端生长半径R，LANGER等［20］引入了R=λC作为稳定界面理论的限制条件，其中λC为最小标准扰动波长.

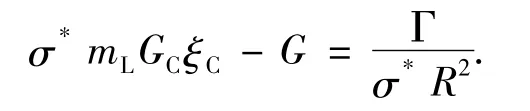
式中:mL为液相线斜率;GC为枝晶尖端液相溶质浓度梯度;ξC为溶质浓度的贝克利系数的函数;G为温度梯度;σ*为定常系数，σ*=1/(4π2);Γ为Gibbs-Thompson系数;R为枝晶尖端半径.

立方晶系的金属晶体的择优生长方向为［100］方向，凝固过程中枝晶尖端前沿过冷度ΔT由4部分组成:

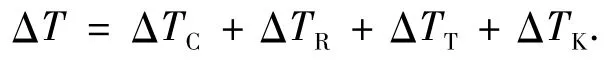
式中:ΔT为枝晶尖端过冷度;ΔTc为成份过冷度; ΔTR为曲率过冷度;ΔTT枝晶尖端动力学过冷度; ΔTK为溶质扩散过冷度.

鉴于双辊连续铸轧是亚快速凝固(冷却速度102～103℃/s)过程的原因，因此相对于快速凝固过程的枝晶生长速度不是很高.因为生长动力学系数很大，枝晶尖端生长动力学过冷度可以忽略.此外，由于凝固在准平衡状态下进行，可以认为合金的平衡分配系数、液相中溶质的扩散系数保持不变.因此可对KGT模型进行修正，修正后的KGT模型为

式中:C0为合金初始质量浓度;K0溶质平衡分配系数;σ为界面能;ΔSf为溶液体积熵;Pe为溶质浓度的贝克利系数;Iv(pe)为pe的伊万卓夫函数.

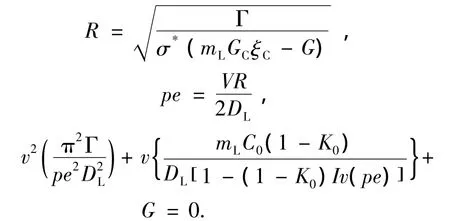
通过上述公式求解可以获得枝晶生长速度v和枝晶尖端半径R，故可以采用修正的KGT模型来描述枝晶生长过程.

1.4 溶质分布模型

为了揭示溶质再分配与微观组织演变过程的关系，必须考虑模拟计算域内的溶质分布问题.因此本文在改进的三维CA模型中加入了溶质场计算模型.固/液界面作为连接两相的边界条件来处理.为减少计算量，溶质浓度场的计算可以直接在微观元胞内完成，对溶质分配进行必要的简化处理.采用刘永刚等［21］提出溶质扩散方程来描述:

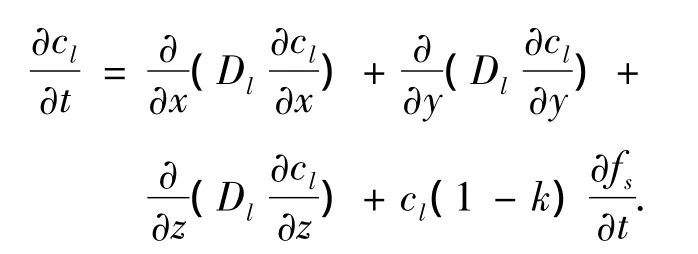
固液相界面平衡浓度的控制方程为

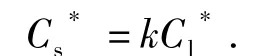
式中:k为溶质分配系数;Cs*，Cl*分别为固/液界面上固相和液相的平衡浓度.

固相份数为fs的元胞的界面曲率控制方程为

式中:N为邻位元胞数量，a为元胞尺寸.

2 元胞自动机-有限元模型

2.1 基于CA的双辊连铸凝固组织的仿真模型

结合现有的随机性与确定性方法，借鉴Gandin和 Rappaz等［16，17］提出的元胞自动机(Cellular Automaton)模型，就可以实现对双辊薄带连铸凝固组织形成的动态模拟.

将凝固区域划分为四边形或六边形网格，然后将每个网格单元划分成更细而均匀的节点，所有节点在凝固前置为液态Pi=0(表示液态)，选取时间步长δt.当单元温度低于液相线时，开始形核，在δt时间内温度下降δT，过冷度相应增加δT，(这时δT/δt的值可通过宏观的工艺条件加以控制)，此时熔体内新生晶核的密度为

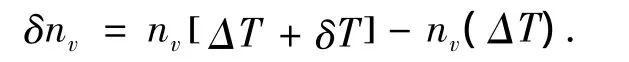
nv的值可通过Oldfield的连续形核模型得到，这些新的晶核在所有CA单元上随机分布，其形核率为

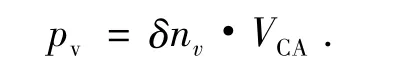
式中，VCA为单个CA单元的体积.在δt时间内，每个CA单元被赋予一个随机数r(0≤r≤1)，如果一个单元仍为液态，当满足r≤Pv，该单元变为固态，其qi值被赋予一个正整数(该数对应一个晶向指数，表明生长的各向异性).形核后按一定规律生长，假定其按枝晶尖端动力学规律生长，晶粒的最大生长方向与CA单元中的X轴夹角为θ，那么t时刻晶粒的半径即四边形的半对角线长:

枝晶尖端的生长规律v［ΔT(t')］可以根据KGT模型得出.图l为CA模型示意图，从tA时刻到tB，由A节点形核长大的四方形晶粒接触到四个相邻单元B1、B2、B3、B4.这时晶粒半对角线长LtB与lθ=(cosθ+|sinθ|))相等，l为CA网格单元间距.

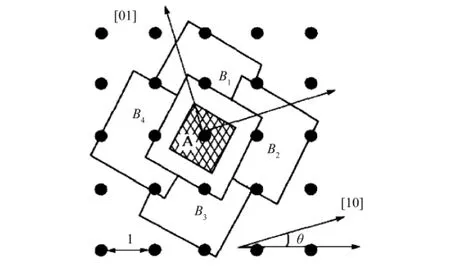
图1 Cellular Automaton模型示意图

CA模型规定此时单元B1～B4凝固，其索引值qi被赋予一个与原始节点A相同的整数.这样晶核就开始长大，并通过不断捕获周围的液态单元而成为最终的晶粒.B的4个单元节点继续长大，将在下一时刻捕获B周边的8个节点，依此类推.晶粒按照枝晶的尖端长大速率而增大.但在晶粒长大过程中，晶粒偏离了原始晶向，所以在每一步模拟中还要对枝晶长大方向进行校正.

2.2 宏观温度场有限元计算模型

双辊连续铸轧纯铝工艺示意图如图2所示［22〛.因为采用水平式同径双辊铸轧进行模拟实验，因注水口的宽度几乎等于铸辊的宽度，可以将双辊薄带连铸过程的模拟简化为二维问题.铸轧区域是对称分布的，为了减少有限元计算量，只需要计算对称面的一半即可.应用元胞自动机模型模拟连续铸轧过程中金属凝固过程需要和有限元法相耦合.一个简单的有限元网格模型如图3所示.有限元网格被分割为m×n个网格，网格中的每个节点的坐标为(i，j)，当元胞状态是液态时被赋予0，当元胞状态是固态时被赋予1.

图2 铝双辊连续铸轧示意图

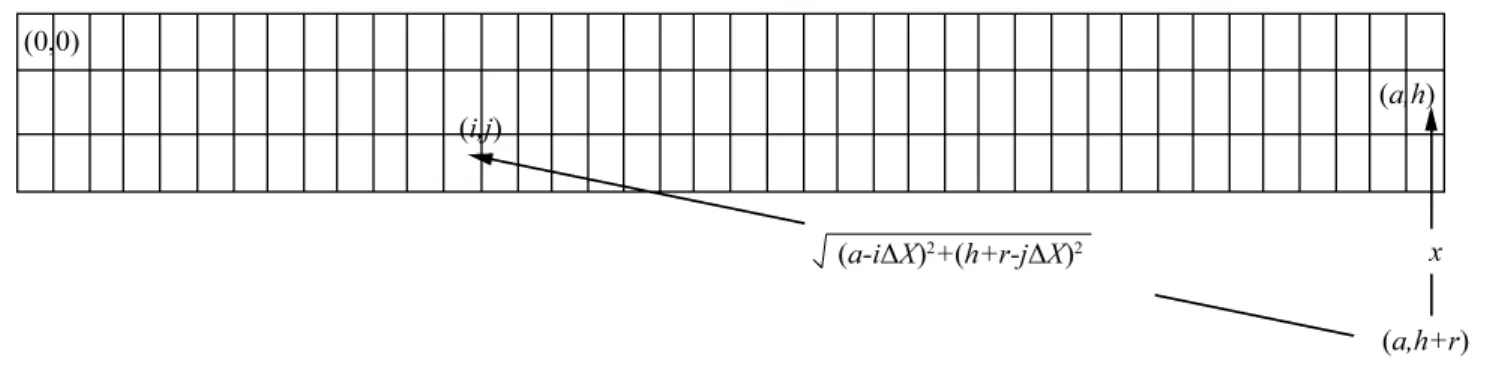
图3 计算元胞模型

随着金属凝固过程的进行，固相率ΔfS(i，j)不断发生变化.利用二维m×n网格来表示每个元胞的固相率fS(i，j)和固相率增量ΔfS(i，j).随着凝固微观组织的形成，各个元胞的固相率在逐渐增加，当元胞的固相率fS(i，j)≥1时，液相将转化为固相.凝固组织的形成和凝固动力学演变可以通过元胞状态的改变来获得.当网格节点(i，j)和(a，h+r)之间的距离满足下式时，节点(i，j)可以作为计算区域的节点.

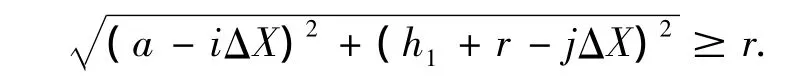
式中:a为铸轧区长度;2h1为出口铝带坯厚度;r为铸轧辊半径;ΔX为正方形元胞的边长.其中，

根据上述方程，只要网格数量m×n确定，如输入a，r和h1等参数到操作程序中就可以再现双辊连续铸轧薄带凝固微观组织演变过程和晶粒大小及分布.

3 模拟结果与讨论

为验证所建数学模型的可行性，对双辊连续铸轧工业纯铝在不同工艺条件下的凝固过程进行进行了模拟研究.模拟计算模型如图4所示［23］，对铸轧区域内的宏观温度场的计算模型采用如图3所示的网格划分.无特别说明外，所有模拟采用的形核参数如表1所示，环境温度为20℃，铸轧薄带的厚度为6mm.计算模拟所需工业纯铝的物性参数如表2所示.

表1 CA－FE模拟用的形核参数

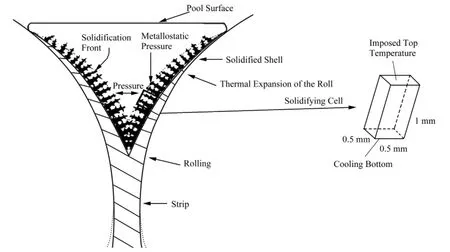
图4 双辊连铸薄带凝固组织模拟计算示意图

表2 工业纯铝的物性参数

3.1 铸轧速度对双辊连续铸轧纯铝凝固微观组织的影响

在其他条件不变的情况下，对于不同的铸轧速度采用移动边界法，铸轧区与铸辊表面的传热采用相应的函数来处理.对三种不同的铸轧速度对双辊连续铸轧工业纯铝的凝固晶粒组织进行了相应的模拟.不同铸轧速度的模拟方案如表3所示.

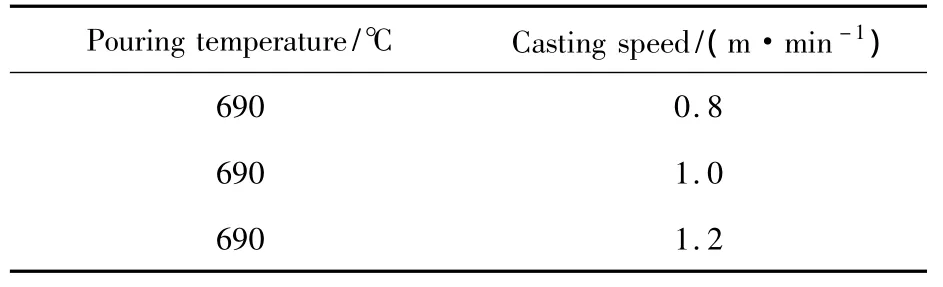
表3 不同铸轧速度的模拟方案

不同铸轧速度下，双辊连续铸轧纯铝的三维凝固组织及纵向凝固组织如图5、6所示.

图5 不同铸轧速度下三维凝固组织a－c铸轧速度分别为0.8，1.0，1.2m/min

从图5、6可知，铸轧速度越低时，铸轧区与铸 轧辊的接触时间长，散热时间长，相当于铸轧区与铸辊表面的换热系数很大，因此铸轧辊表面形成的晶粒很细小，表层细晶区很薄，不是很明显，柱状晶的比例较大，且其一次枝晶较粗.随着铸轧速度的增大，表面等轴晶逐渐变得粗大，熔体的温度梯度降低，不利于柱状晶的生长，将会较早发生柱状晶向等轴晶的转变;同时由于冷却速度增大，最终获得含有细小的柱状晶和等轴晶的混合凝固组织.可见，提高铸轧速度是获得细晶的一种很好的方法.

图6 不同铸轧速度下y=0.25mm截面的凝固组织a－c铸轧速度分别为0.8，1.0，1.2m/min

3.2 形核速率分布标准方差对双辊连续铸轧纯铝凝固微观组织的影响

形核速率分布标准方差是指形核过冷度范围的宽窄，形核速率分布标准方差越大，表示发生形核的过冷度范围越大.在给定最大形核密度时，随着形核速率分布标准方差的减小，说明开始形核的过冷度增大，形核结束时的过冷度减小，发生形核过冷度的范围由宽变窄，这样有利于形成细小而均匀的凝固晶粒组织.参考梁作俭等［24］的研究，本文对四种不同的形核速率分布标准方差对双辊连续铸轧工业纯铝的凝固晶粒组织进行了相应的模拟.不同形核速率分布标准方差的模拟方案如表4所示.

表4 不同形核速率分布标准方差模拟方案

不同形核速率分布标准方差下，双辊连续铸轧纯铝的三维凝固组织及纵向截面上的凝固组织分别如图7、8所示.

从图可知，形核速率分布标准方差的改变对凝固晶粒组织的影响很小.凝固组织是由柱状晶和等轴晶组成的混晶组织，晶粒大小均匀.可能是因为采用随机性形核模型，形核速率分布标准方差会在一定范围内变化，从而对最终形成的凝固晶粒组织影响甚微.

图7 不同形核速率分布标准方差下的三维凝固组织a－d形核速率分布标准方差分别为0.8，1.0，1.4，2.0K

4 实验验证

以双辊连续铸轧工业纯铝为研究对象，采用水平式同径双辊铸机进行实验验证，因注水口的宽度几乎等于铸轧辊的宽度，同时采用侧封板绝热和加热装置，可以将双辊薄带连续铸轧过程的模拟简化为二维问题.同时和相同条件下的实验结果进行比较，以验证所建立的微观数学模型的可靠性.在浇注温度为690℃、铸轧速度1.0m/min、熔池高度40mm时铸轧出的纯铝薄带凝固组织如图9所示.

对比模拟结果和实验结果可以看出，无论从晶粒形貌、表层细晶区和柱状晶区域的大小，还是柱状晶向等轴晶的演变来看，模拟结果都基本与实验结果吻合.从模拟和实验结果还能看出，凝固过程中并没有得到穿晶组织，有中心等轴晶的出现，这主要是由于模型底部的换热系数较小，降低了中心熔体的温度梯度，使中心熔体的过冷区域和过冷度都增大，阻碍柱状晶的继续长大，有利于形成中心等轴晶.说明建立的CA-FE模型可以模拟和预测双辊连续铸轧工艺参数对凝固微观组织的影响，对于优化连续铸轧工艺参数和提高铸轧产品质量具有重要的理论和实践意义.

图8 不同形核速率分布标准方差下y=0.25mm截面的凝固组织a－d形核速率分布标准方差分别为0.8，1.0，1.4，2.0K

图9 浇注温度为690℃、铸轧速度1.0m/min、熔池高度40 mm时的实验条件下啮合点前铸轧纯铝薄带凝固组织(a)横向晶粒组织; (b)纵向晶粒组织

5 结论

(1)建立了双辊连续铸轧纯铝薄带凝固过程的数学物理模型，采用一种改进的元胞自动机(CA)法，对双辊连续铸轧纯铝薄带进行了凝固微观组织模拟.

(2)耦合了宏观温度场、三维溶质场计算及微观组织模拟计算，考虑了溶质扩散、曲率过冷和各向异性等重要因素对枝晶生长的影响，定义了界面单元捕获规则，能够模拟凝固过程中枝晶生长的形态.可以再现凝固过程中晶粒组织的形成及转化.

(3)模拟了连续铸轧工艺参数(浇注温度、铸轧速度)对双辊连续铸轧纯铝薄带凝固微观组织的影响规律，对于指导生产有实际意义.

(4)以双辊连续铸轧工业纯铝为研究对象，对特定实验工艺条件的凝固过程进行了微观组织模拟和实验对照，模拟结果与金相观察符合较好.

［1］ 张纬栋，任三兵，杜锋，等.双辊薄带连铸布流系统的数理模拟［J］.过程工程学报，2010，10(z1):256 -259.

［2］ 王波，张捷宇，张胤，等.双辊薄带连铸过程数学物理模拟研究［J］.内蒙古科技大学学报，2008，27 (1):67-72.

［3］ BAE J W，KANG C G，KANG S B.Mathematical model for the twin roll type strip continuous casting of magnesium alloy considering thermal flow phenomena［J］.Journal of Materials Processing Technology，2007，191 (1-3):251-255.

［4］ FANG Yuan，WANG Zhenmin，YANG Qingxiang，el at.Numerical simulation of the temperature fields of stainless steel with different roller parameters during twin-roll strip casting［J］.International Journal of Minerals，Metallurgy and Materials，2009，16(3):304-308.

［5］ ZHAO Hu，LI Peijie，HE Liangju.Coupled analysis of temperature and flow during twin-roll casting of magnesium alloy strip［J］.Journal of Materials Processing Technology，2011，211(6):1197-1202.

［6］ FLEMINGS M C，CALM R W.Organization and Trends in Materials Science and Engineering Education in the US and Europe［J］.Acta Materialia，2000，48(1):371 -383.

［7］ BOETTINGER W J，CORIELL S R，GREER A L.Solidification Microstructures:Recent Developments，Future Directions［J］.Acta Materialia，2000，48(1):43 -70.

［8］ 许庆彦，冯伟明，柳百成，等.铝合金枝晶生长的数值模拟［J］.金属学报，2002，38(8):799-803.

［9］ BELTRAN-SANCHEZ L，STEFANESCU D M.Growth of solutal dendrites:A cellular automaton model and its quantitative capabilities［J］.Metallurgical and Materials Transactions A，2003，34(2):367-382.

［10］ BELTRAN-SANCHEZ L，STEFANESCU D M.A quantitative dendrite growth model and analysis of stability concepts［J］.Metallurgical and Materials Transactions A，2004，35(8):2471-2485.

［11］ RAGHAVAN S，KRANE M J M，JOHNSON D R.Modeling of Casting［C］\Modeling of Casting，Welding and Advanced Solidification Processes-X，Destin:TMS，2003: 107-111.

［12］ 李 强，李殿中，钱百年.枝晶凝固过程中的溶质浓度分布模拟［J］.金属学报，2004，40(11):1215 -1220.

［13］ 朱鸣芳，戴 挺，李成允，等.对流作用下枝晶生长行为的数值模拟［J］.中国科学E，2005，35(7): 673-688.

［14］ WANG W，LEE P D，MCLEAN M.A model of solidification microstructures in nickel-based superalloys: predicting primary dendrite spacing selection［J］.Acta Materialia，2003，51(10):2971-2987.

［15］ XIONG Shoumei，XU Qingyan，KANG Jinwu.Modeling and Simulation Technology in Casting Process［M］.Beijing:China Machine Press，2004:140-145.

［16］ GANDIN C A，RAPPAZ M.A coupled finite elementcelluar automaton model for the prediction of dentritic grain structures in solidification processes［J］.Acta Materialia，1994，42(7):2233-2246.

［17］ PAPPAZ M，GANDIN C A.Probabilistic modelling of microstructure formation in solidification processes［J］.Acta Metallurgica et Materialia，1993，41(2): 345-360.

［18］ KURZ W，GIOVANOLA B，TRIVEDI R.Theory of microstructural development during rapid solidification［J］.Acta Metallurgica，1986，34(5):823-830.

［19］ RAPPAZ M，THEVOZ P H.Solute diffusion model for equiaxed dendritic growth:Analytical solution［J］.Acta Metallurgica，1987，35(12):2929-2933.

［20］ LANGER J S，MULLER-KRUMBHAAR J.Stability effects in dendritic crystal growth［J］.Journal of Crystal Growth，1977，42:11-14.

［21］ 刘永刚，陈军，潘冶，等.Al-4.5%Cu合金凝固过程显微组织的数值模拟①［J］.中国有色金属学报，2002，12(6):1130-1135.

［22］ LIU Xiaobo，XU Qingyan，JING Tao，et al.Simulation of microstructures in solidification of aluminum twinroll casting based on CA［J］.Transactions of Nonferrous Metals Society of China，2009，19(2):422-427.

［23］ WANG Bo，ZHANG JieYu，LI XiangMei，et al.Simulation of solidification microstructure in twin-roll casting strip［J］.Computational Materials Science，2010，49:S135–S139.

［24］ 梁作俭，许庆彦，李嘉荣，等.单相合金凝固过程微观组织的三维数值模拟［J］.金属学报，2004，40 (4):439-444.

Numerical simulation of microstructures evolution of aluminum twin-roll continuous casting based on a modified CA method

CHEN Shou-dong，CHEN Jing-chao，PENG Ping
(Key Laboratory of Advance Material of Rare Precious and Nonferrous Metals of Education Ministry of China，Key Laboratory of Advanced Materials of Yunnan Province，Kunming University of Science and Technology，Kunming 650093，P.K.China)

A new mathematic model for the nucleation and dendritic growth of twin-roll continuous casting pure aluminum thin strip during solidification process was developed，which was based on cellular automaton(CA)-finite element(FE)method and the classical transfer equations during dendritic growth.The model coupled the temperature field calculation and microstructure simulation.The solute diffusion，curvature undercooling and anisotropy were also considered in the model，all of which have significant influence on the dendrite evolution.By setting up the CA cell capturing rules，the dendritic growth morphology can be simulated.Applications of the model in equiaxed dendritic growth，multiple equiaxed dendritic growth，and columnar grain growth，transformation of columnar dendrite to equiaxed dendrite in solidification of twin-roll continuous casting pure aluminum thin strip solidification were presented.The microstructure simulation results were compared with the experimental results and they were in good agreement in dendritic morphology，which validated the correctness of the proposed model.

pure aluminum;twin-roll continuous casting;solidification microstructure simulation;cellular automaton(CA)-finite element(FE)method;dendrite morphology

TG249.7;TG244.3;TB115 文献标志码:A 文章编号:1005-0299(2012)06-0073-08

2011-12-30.

新国家自然科学联合基金(u0837601)，新国家基金号(50874054)，云南省创新团队(2009CI003)，云南省自然科学基金(2008CD087).

陈守东(1987-)，男，硕士.

陈敬超，E-mail:chenjingchao@kmust.edu.cn

(编辑 张积宾)