静电纺丝运动轨迹的建模与仿真研究

杜海英，王 兢，王 娟

(1.大连理工大学电子科学与技术学院，辽宁大连116023;2.大连民族学院机电信息工程学院，辽宁大连116600)

静电纺丝运动轨迹的建模与仿真研究

杜海英1，2，王 兢1，王 娟2

(1.大连理工大学电子科学与技术学院，辽宁大连116023;2.大连民族学院机电信息工程学院，辽宁大连116600)

静电纺丝作为一种简单而有效的方法，广泛应用于纳米纤维的制备.本文以静电纺丝过程中带电溶液为对象，将带电溶液模拟成多个离散化的带电粒子，对带电粒子进行受力分析，建立带电粒子的分子动力学模型.基于Runge-Kutta算法，对带电粒珠的运动轨迹进行了数值计算，并利用MATLAB软件进行了仿真.改变静电纺丝工艺参数，得到了带电粒珠的不同运动轨迹的仿真图像.在相同的工艺条件下进行了纺丝实验，实验所制备的纳米纤维轨迹与仿真图像相一致.分析结果表明，静电纺丝过程中，改变工艺参数可以实现纳米纤维的运动轨迹的可控.

静电纺丝;纳米纤维;仿真;分子动力学模型

随着纳米纤维的广泛应用，其制备技术也得到了业界的广泛关注，成为纳米材料的研究热点.纳米纤维的制备方法有很多，主要有提拉法［1］、模板聚合法［2］、相分离法［3-5］、水热合成法［6，7］、自组装法［8］、静电纺丝法［9］等.静电纺丝法是一种简单而有效的通过静电力作用制备纳米纤维的方法［10，11］.通过静电纺丝法制备的纳米纤维具有非常优异的物理特性，在过去的几十年里，静电纺丝技术主要用来合成有机高分子聚合物［12］，近年来，静电纺丝技术也被用于合成无机纳米材料，例如 SnO［13，14］，InO［15，16］，TiO［17］，WO［18］，

22323 ZnO［19］，Co3O4［20］，BaTiO3［21］等.此外，通过控制静电纺丝工艺参数，可以制备出不同形貌的纳米纤维，包括纳米线［22］、纳米管［23］、纳米带［24］、纳米棒［25］等新颖结构.

静电纺丝装置通常由三部分组成:高压电源，带喷丝头的容器，收集装置.喷丝头和收集装置作为高压电源的两极，如图1所示.在静电纺丝过程中，首先将配置好的有机溶液注入带有喷丝头的容器中，调节溶液的黏度和流动速度，打开电源，在喷丝口与接收装置之间形成梯度电场，喷丝口处的溶液液滴会在重力、电场力、表面张力、粘弹力、库仑力等几个力的相互作用下在喷丝口形成“泰勒锥”［26］，当电场强度超过某一阈值时，电场力将会克服表面张力，在喷丝口处产生纤维式的喷射细流.在纤维向收集装置运动过程中，由于一系列弯曲不稳定过程和静电拉伸过程，纤维逐渐劈裂，同时溶剂挥发，直径不断减小，随后干燥的聚合物纳米纤维无序的沉积到收集装置上，形成无纺布式的二维纳米结构.

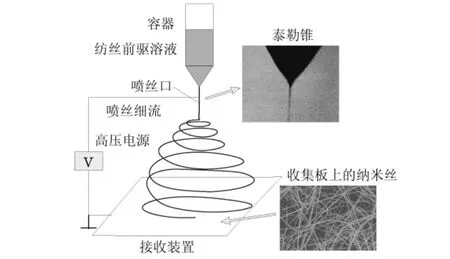
图1 静电纺丝装置示意图

在纺丝过程中，影响纤维运动轨迹及纤维形貌的因素有很多，从静电纺丝工艺角度来分析，主要分为两类:一类是溶液的性质，包括溶液的粘度、浓度、表面张力以及电导率;另一类是操作参数，包括纺丝过程施加的电压、空间电场分布、磁场分布、溶液流速、喷丝口到收集装置的距离、空气温度、湿度、气压等环境因素，这些参数的改变都会影响纺丝过程中聚合物纤维的运动轨迹及纤维的形貌.其中有些参数是可控的，有些参数是不可控的，此外在装置中引入一个外部磁场用来改变喷射流的受力状态，从而实现对纺丝轨迹的控制.本文利用通电线圈来引入外加磁场，将静电纺丝溶液喷射细流模拟为离散化的带电粒子，对带电粒子进行受力分析，建立其分子动力学模型，分析其运动轨迹，通过MATLAB仿真与实验对比，就电场电压、纺丝距离、外加磁场等主要参数对纺丝轨迹及纤维形貌的影响进行了分析，结果表明，在外加电场，磁场一定的条件下静电纺丝过程中纳米纤维的运动轨迹是可控的.

1 建模

在静电纺丝过程中，纺丝溶液在高压静电场中受到电场力、库仑力、表面张力等外力的作用，形成发散喷射细流，将喷射流体模拟成多个离散的带电粒子，这些带电粒子可视为不计质量的物质点连接而成，质点的运动及质点间的运动如图2所示［27］.图2为静电纺丝过程中，质点组成的喷射流模型，将喷射细流视为无穷小的紧密相邻的无穷多个流体质点组成.质点的运动过程主要分为两个阶段，直线运动阶段和不稳定运动阶段.喷射流在高压静电场的作用下，从喷丝孔喷出，沿直线做加速运动，在加速运动过程中，粘性阻力也随之变大，当粘性阻力达到甚至超过电场力时，喷射流将会变得不稳定，此时，喷射流的加速度变成零，空气中的微小扰动都会导致喷射流偏离平衡位置，进行不稳定运动阶段，其运动轨迹主要由这两个阶段质点的受力状态决定［28］.

图2 静电纺丝过程中质点组成的喷射流模型

1.1 喷射细流离散化

在外加磁场作用下，喷射流模拟成多个离散的带电粒子，每个粒子带电量为e，质量为m.喷射流的连续的粒子i，i+1，i-1，其中与粒子i+1和粒子i-1有关的变量参数，分别用下标p和q表示.粒子i的坐标为(xi，yi，zi)为时间t的函数.连接粒子i和粒子i+1链长为lpi，连接粒子i和i -1的链长为lqi，三粒子间的两段链长分别如下式(1)，(2)所示:

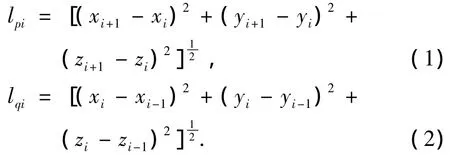
任意两粒子i和j之间的距离可表示为式(3)所示:

1.2 离散化后的受力分析

喷射细流上任意带电粒子都会受到极板之间的电场力fe，两粒子间的库仑力fc，由于溶液粘性束缚作用的粘弹力fv，由磁场引起的洛仑兹力fl，及表面张力fs.其受力分析如图3所示.

图3 带电粒子在电场中的运动轨迹示意图

其他粒子作用在粒子i上的库仑力fc净值为

其中Vo为静电中所加高压静电场的电压，h为喷丝口到接收板的距离.

静电纺丝过程中有机溶液的粘度对纳米纤维的粗细有很大的影响，作用在粒子上的粘弹力是影响纺丝轨迹的一个重要参数，一般情况下，作用在粒子i上的粘弹力fv净值为

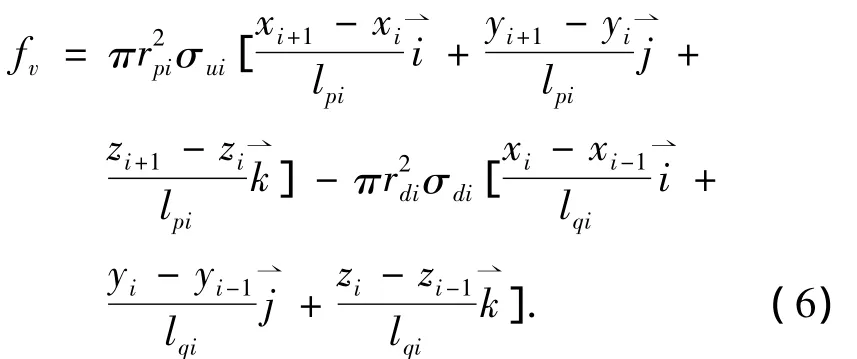
在计算过程中，连接粒子的物质被看成圆柱体，其半径为相应段喷射流半径，由质量守恒定律可知

其中api和aqi分别是lpi和lqi的喷射流半径，a0和L分别为喷射流的初始半径和初始长度.作用在粒子i上的表面张力fs起到了保持喷射流直线状的作用，其值为

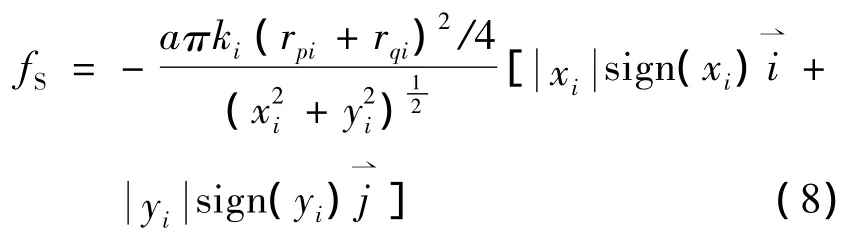
其中a为表面张力系数;ki为喷射流在粒子i处得曲率;可以近似由三个粒子i+1，i，i-1的坐标值计算得到;‘sign(x)’为符号函数，其取值如式(9)所示:

其中B为磁场强度，方向指向喷丝口的轴线.

1.3 数学模型的建立

由牛顿第二定理，无外加磁场作用下，忽略外磁场力(洛仑兹力的作用)的影响，结合上述各作用力，得到粒子i所受合力fH应满足方程(11):

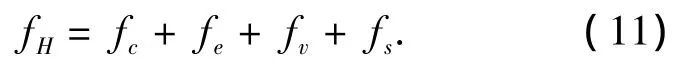
将上式整理得出粒子i的运动满足方程(12).

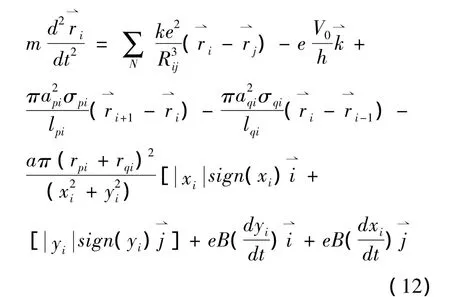
在静电纺丝过程中，如果考虑带电粒子运动所引起的感应磁场的影响，或在环境中引入外加磁场的作用，则带电粒子同时还会受到一个垂直运动方向的指向喷丝口轴线方向的洛仑兹力fq的作用，其大小为

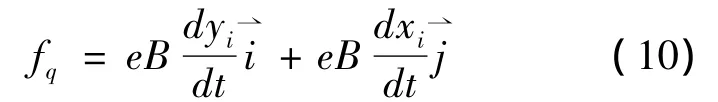
⇀⇀=x⇀i

其中ri表示粒子i的坐标向量，表示为:rii

+yi⇀j +zi⇀k，根据坐标位置(xi，yi，zi)，可以计算出

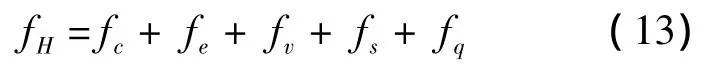
2 静电纺丝过程仿真

分别在外加磁场和无磁场的作用下得到两个带电粒子运动的分子动力学模型，利用Matlab软件对已经建立的数学模型进行数值计算.采用Runge-Kutta算法，选取适当的步长，代入参数进行计算，得到带电粒子运动轨迹的仿真曲线.

2.1 Runge-Kutta算法

Runge-Kutta算法［29］是一种在工程广泛应用的高精度单步算法，采取措施对误差进行抑制，所以实现原理相对复杂.它的基本思想是从(xi，yi)点出发，以某一斜率沿直线达到(xi+1，yi+1)点，利用函数f(x，y)在某些点处值的线性组合构造公式，将构造的公式按泰勒公式展开后与初值问题的解的泰勒公式展开做比较，使其有尽可能多的相同项，确定其中参数，从而保证构造公式具有较高的精度.

对于y'=f(x，y)的一阶常微分方程，平均斜率记为:K*=f(xi+θh，y(xi+θh)，)其中0＜θ＜1，h=xi-xi-1为步长.则K*成为区间［xi，xi+1］上的平均斜率.在一阶精度的欧拉公式中，取点xi的斜率K1=f(xi，yi)作为平均斜率K*，则有yi+1= yi+hK1，精度很低.当用点 xi处的斜率 K1与点xi+1处的斜率K2的算术平均值作为平均斜率的近似值，就会得到二阶精度的改进的欧拉公式:K1= f(xi，yi)，K2=f(xi，yi+hK1)，yi+1=yi+h(K1+ K2)/2，依次类推，如果在区间［xi，xi+1］内多预估几个点上的斜率K1，K2，K3…Km，并用它们的加权平均数作为平均斜率K*的近似值，显然能构造出具有很高精度的高阶计算公式.经数学推导、求解，就可得到在工程广泛应用的四阶Runge-Kutta算法:yi+1=yi+h(K1+2K2+2K3+K4)/6，K1=f(xi，yi)，K2=f(xi+h/2，yi+hK1/2)，K3=f (xi+h/2，yi+hK2/2)，K4=f(xi+h，yi+hK3). Runge-Kutta算法也用于求解带初值的常微分方程组，如y1

’=f1(x，y1，… ym);y2’=f2(x，y1，…ym);…;ym

’=fm(x，y1，…ym)a≤x≤b，微分方程的初始条件:y1(a)=η1，…，ym(a)=ηm，t=a将定义区间［a，b］离散化，步长为h=(b-a)/M，xj+1=xj+h，j=0，1，…M-1，x0=a.记yi(j)=yi(tj)，并且y0

(0)=a.基于四阶的Runge-Kutta算法，运用Matlab软件进行编程计算，可求得微分方程组的数值解.基于Runge-Kutta算法求解方程的Matlab软件的计算流程如图4所示.

2.2 喷射流运动轨迹的模拟

将喷射流看成由N个带电粒子相连，喷射流底部的粒子记为i=1，顶部的粒子记为i=N.粒子个数N随着喷射流的运动而变化.在t时刻，如果第N个粒子与喷丝口之间的距离超过h/ 20000，则喷射流的顶部增加一个粒子，即N=N+ 1，同时给定增加粒子的初始位置(为了模拟喷射流的螺旋运动轨迹，给每个粒子施加一个扰动，ω为扰动频率):xN=10-3L sin(ωt);yN=10-3L cos (ωt);zN=49999h/50000.

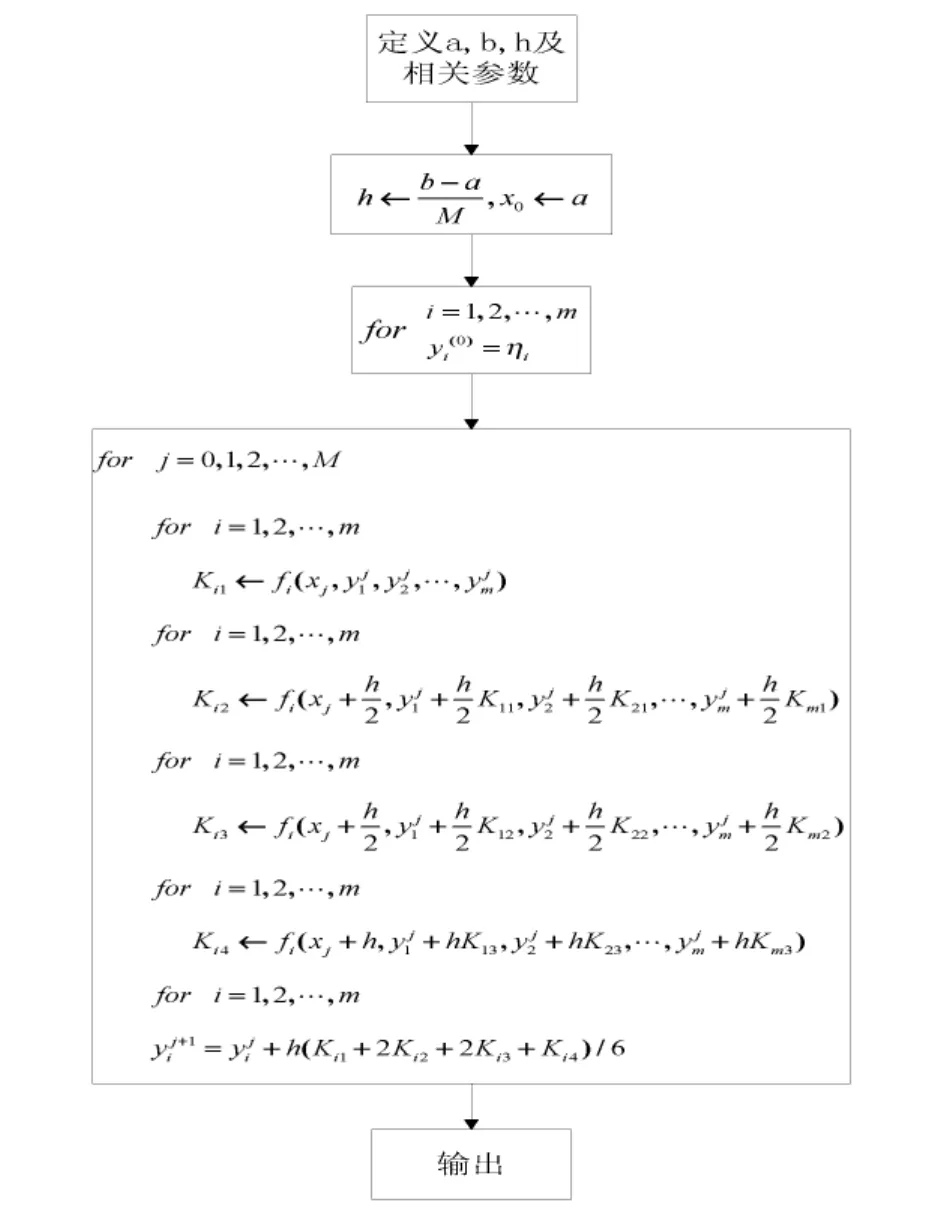
图4 基于Runge－Kutta算法的计算流程图

在计算带电粒子的运动轨迹时，需要进行带电粒子参数的数值计算，给定初值如下:设t=0为带电粒子的初始时刻;喷射流粒子的个数N=2;每个粒子的初始速度为0;设初始时刻粒子的表面电荷密度σdl和σuN，连接粒子之间的链长为ld1和luN均为零，即ld1=0;σdl=0;luN=0;σuN=0.喷射流运动轨迹模型的具体计算流程如图5所示.

3 数值模拟仿真结果与实验分析

在没有外加磁场的作用下，设置带电粒子的质量m=1.84×10-9kg，粒子带电量e=2.0× 10-9C，粘性系数μ=103kg/(ms)，粘性系数弹性模量G=105kg/(ms2)，扰动频率ω=10-4s-1，溶液的表面张力系数为α=0.12 N/m，静电压V0= 15 KV，喷丝口距收集板间距离为30 cm.通过Matlab软件编程计算得到的喷射流随时间变化的运动轨迹如图6所示.其中图6(b)为在相同条件下喷射流运动轨迹的俯视图.可以看出喷射流的运动轨迹近似为一条锥形螺旋线，上端为t=0时刻，随着时间的推移，螺旋线的半径逐渐增大，且喷射流的摆幅度逐渐增大，最终落在接有负极的接收板上.选取ZrOCl2的有机盐溶液为纺丝前驱液，静电压V0=15KV，喷丝口距收集板间距离为20 cm的实验条件下进行纺丝.得到收集板上有机纳米纤维的SEM照片如图7所示.由于扫描电镜观察范围有限，且放大倍数较大，图7中纤维只是单根纺丝中的一部分，可以看出纳米纤维运动轨迹的半径较大，纳米纤维的平均直径约为200 nm，大约每隔20～30 μm发生一次转折，转角约15度，图7中黑线部分标出纺丝纤维转折区域，与仿真轨迹相似.

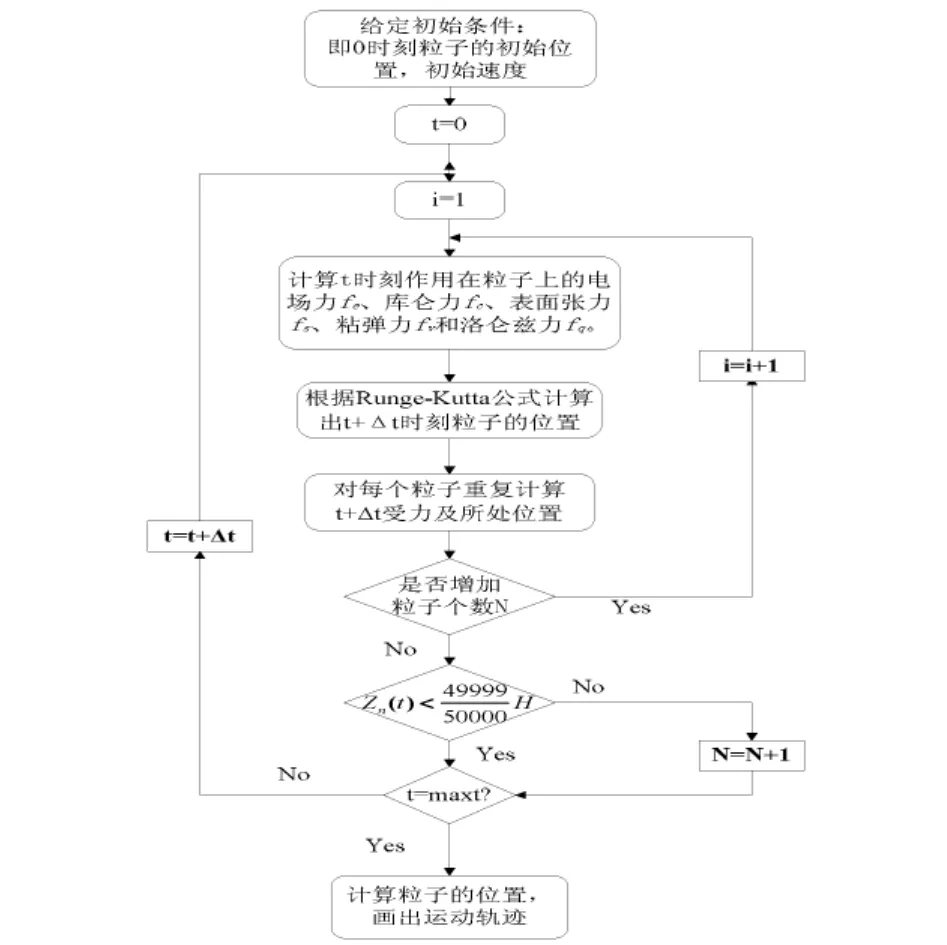
图5 喷射流运动轨迹的计算流程图

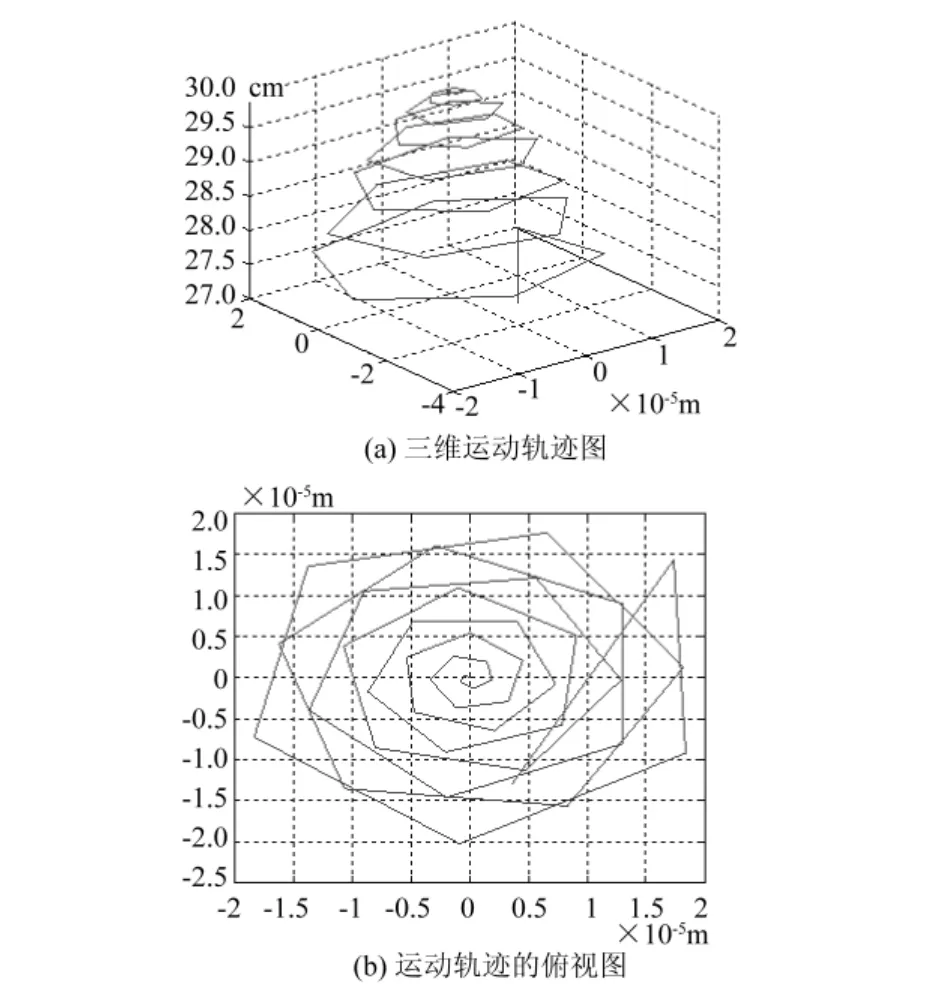
图6 V0=15 KV时喷射流图

改变设置参数，将电场力分别设为V=15KV V=20KV，外加磁场B=3T时，其它参数不变，仿真轨迹的三维图、二维俯视图分别如图8(a)，(b)、图9(a)，(b)所示，从图8可以看出，纺丝轨迹的半径逐渐变小，螺旋线的旋转周数随之变少，螺旋线之间的距离逐渐变大.

图7 V0=15 KV时纳米纤维的SEM照片

图8 V0=15 KV，B=3 T时的喷射流图

选择上述参数配置进行静电纺丝的实验，得到喷射流的真实运动轨迹与喷射流运动的仿真轨迹相似.图10为V0=20 KV，B=3 T时实验条件下得到的纳米纤维的SEM照片.可以看出到落在接收板上的纳米纤维趋于成圆形，或半圆，说明相同面积里接收纺丝轨迹完整，纺丝范围比图7中的纺丝范围小，纺丝轨迹的半径比图7中纺丝轨迹的半径小.纳米纤维的平均直径约为100 nm，大约每隔10μm发生一次转折，转角约30度，图10中黑线部分标出纺丝纤维转折区域，可以看出半周或少半周的螺旋线，与图9中的仿真轨迹相似.

改变磁场强度大小，改变静电压大小，纳米纤维束的半径都随之发生变化，静电压不变，磁场强度变大，洛仑兹力束缚作用增强，纤维束半径变小，螺旋线的旋转周数减少，螺旋线之间的距离增加，纺丝区域变小;反之纤维束半径变大，螺旋线的旋转周数增加，螺旋线之间的距离减小，纺丝区域变大.磁场强度不变，静电压越大，纤维束半径越小，螺旋线的旋转周数减少，螺旋线之间的距离增加，纺丝区域越小，反之亦然.设置六组不同的仿真参数得到六组仿真曲线.仿真参数如表1所示，六组仿真曲线的二维俯视图如图11的A1、B1、C1、D1、E1、F1所示.

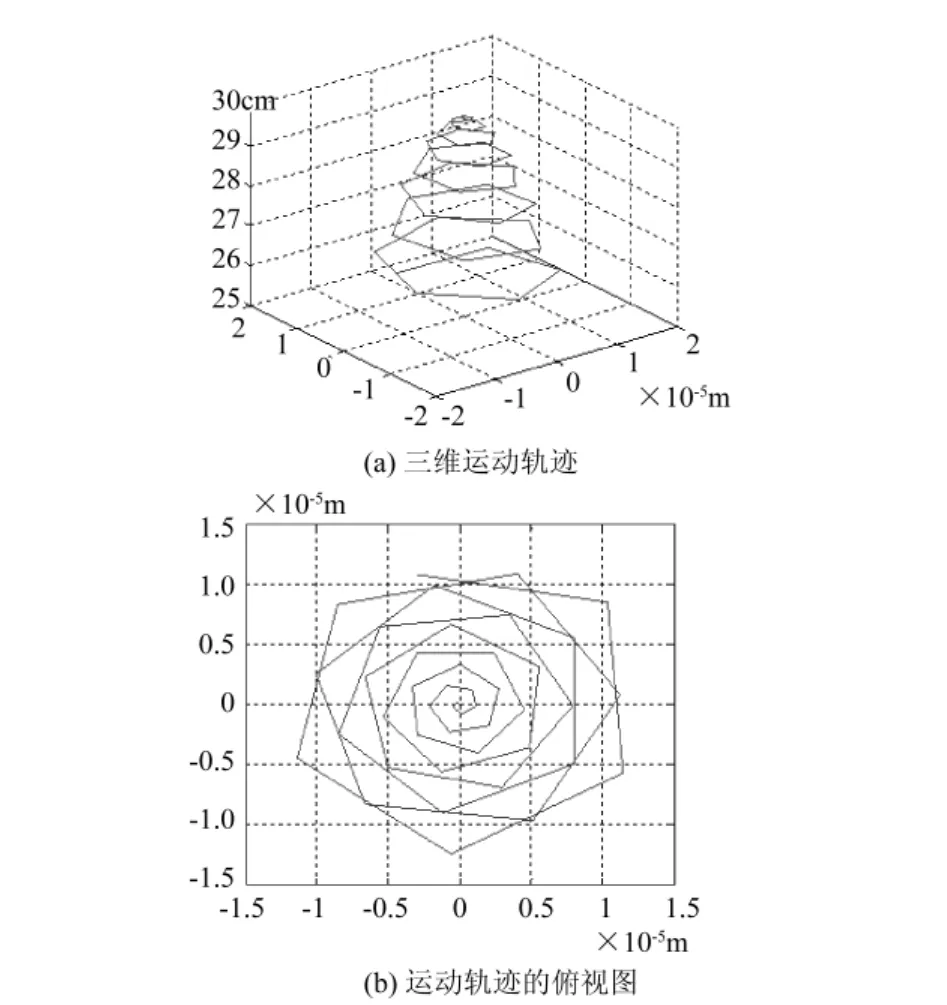
图9 V0=20 KV，B=3 T时的喷射流图

图10 V0=20 KV，B=3 T时纳米纤维的SEM照片

表1 仿真参数对照表

4 结论

通过对带电粒子受力分析，建立出带电粒子的运动轨迹模型，并通过MATLAB软件仿真出静电纺丝过程带电粒子的运动轨迹，该运动轨迹为一条近似的锥形螺旋线，改变仿真参数得到相应仿真轨迹，与真实条件下的纺丝轨迹的SEM照片相一致.外加磁场强度加大，静电压升高，锥形螺旋钱半径减小，螺旋线的旋转周数减少，纺丝区域变小，单根纤维直径变细;反之减小或无外加磁场作用，降低静电压，锥形螺旋线的半径增加，螺旋线的旋转周数增加，纺丝区域变大，单根纤维直径变粗.通过仿真找到最佳的实验参数，控制静电纺丝过程.实现纳米纤维制备过程的可控.目前，单根纤维的直径的大小并没有实现仿真，只是通过SEM照片观察到了纤维的直径的变化，实验中还发现，纤维的粒径也随外加磁场和电压的改变而改变，同时环境湿度、温度及不同的前驱液都会不同程序的影响纳米纤维的运动轨迹及形貌，相关的仿真及实验研究工作有待进一步开展.

［1］ ONDARCUHU T，JOACHIM C.Drawing a single nanofibre over hundreds of microns［J］.Europhysics Letters，1998，42(2):215-220.

［2］ NGUYEN D H，NGUYEN V Q，YOUSUK C，et al.An ammonia gas sensor based on non-catalytically synthesized carbon nanotubes on an anodic aluminum oxide template［J］.Sensors and Actuators B，2007，127: 447-454.

［3］ YIN W Y，WEI B Q，HU C W.In situ growth of SnO2nanowires on the surface of Au-coated Sn grains using water-assisted chemical vapor deposition［J］.Chemical Physics Letters，2009，471:11-16.

［4］ XIE J，LI P，LI Y T，et al，Morphology control of ZnO particles via aqueous solution route at low temperature［J］.Materials Chemistry and Physics，2008，114:943-947.

［5］ TSUYOSHI H，NOBUAKI Y，MASAYOSHI U，et al.Synthesis and H2gas sensing properties of tin oxide nanohole arrays with various electrodes［J］.Sensors and Actuators B，2006，113:852-856.

［6］ XU J Q，JIA X H，LOU X D，et al.Selective detection of HCHO gas using mixed oxides of ZnO/ZnSnO3［J］.Sensors and Actuators B，2007，120:694-699.

［7］ RUAN Q J，ZHANG W D.Preparation and gas sensing properties of p-type La-Bi-Fe-O nanorods［J］.Materials Letters，2008，62:4303-4305.

［8］ KIM H R，CHOI K I，LEE J H，et al.Highly sensitive and ultra-fast responding gas sensors using self-assem-bled hierarchical SnO2spheres［J］.Sensors and Actuators B，2009，136:138-143.

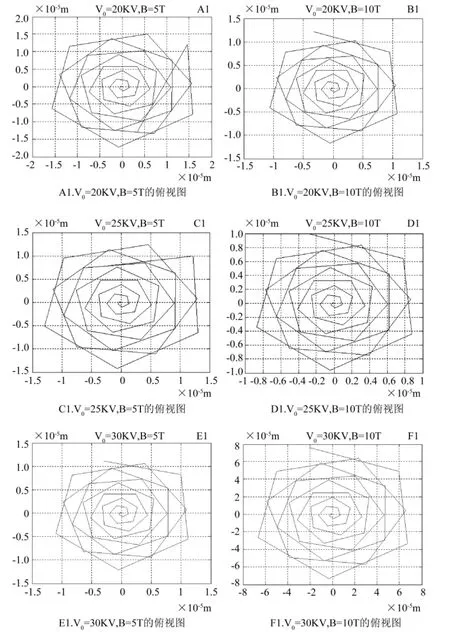
图11 六种纺丝条件仿真曲线

［9］ TEO W E，RAMAKRISHNA S.Electrospun nanofibers as a platform for multifunctional，hierarchically organized nanocomposite［J］.Composites Science and Technology，2009，69:1804-1817.

［10］ LU X，ZHANG W，WANG C，et al.One-dimensional conducting polymer nanocomposites:Synthesis，properties and applications［J］.Progress in Polymer Science，2011，36:671-712.

［11］ WU X J，ZHU F，MU C，et al.Electrochemical synthesis and applications of oriented and hierarchically quasi-1D semiconducting nanostructures［J］.Coordination Chemistry Reviews，2010，254:1135-1150.

［12］ HUANG Z M，ZHANG Y Z，KOTAKI M，et al.A review on polymer nanofibers by electrospinning and their applications in nanocomposites［J］.Composites Science and Technology，2003，63:2223-2253.

［13］ ZHANG Y，LI J P，AN G M，et al.Highly porous SnO2fibers by electrospinning and oxygen plasma etching and its ethanol-sensing properties［J］.Sensors and Actuators B，2010，144:43-48.

［14］ QI Q，ZHANG T，LIU L，et al.Synthesis and toluene sensing properties of SnO2nanofibers［J］.Sensors and Actuators B，2009，137:471-475.

［15］ LI Z P，FAN Y J，ZHAN J H.In2O3Nanofibers and Nanoribbons:Preparation by Electrospinning and Their Formaldehyde Gas-Sensing Properties［J］.Europe journal of inorganic chemistry，2010:3348-3353.

［16］ LIM S K，HWANG S H，CHANG D，et al.Preparation of mesoporous In2O3nanofibers by electrospinning and their application as a CO gas sensor［J］.Sensors and Actuators B，149，(2010)28-33.

［17］ YU Q Z，WANG M，CHEN H Z.Fabrication of ordered TiO2nanoribbon arrays by electrospinning［J］.Materials Letters，64，(2010)428-430.

［18］ LU X F，LIU X C，ZHANG W J，et al.Large-scale synthesis of tungsten oxide nanofibers by electrospinning［J］.Journal of Colloid and Interface Science，298，(2006)996-999.

［19］ PARK J，MOON J，LEE S，et al.Fabrication and characterization of ZnO nanofibers by electrospinning［J］.Current Applied Physics，9，(2009)S210-S212.

［20］ GUAN H Y，SHAO C L，WEN S B，et al.A novel method for preparing Co3O4nanofibers by using electrospun PVA/cobalt acetate composite fibers as precursor［J］.Materials Chemistry and Physics，82，(2003)1002-1006.

［21］ HE Y，ZHANG T，ZHENG W，et al.Humidity sensing properties of BaTiO3nanofiber prepared via electrospinning［J］.Sensors and Actuators B，146，(2010) 98-102.

［22］ ZHANG Y，HE X L，LI J P，et al.Fabrication and ethanol-sensing properties of micro gas sensor based on electrospun SnO2nanofibers［J］.Sensors and Actuators B，132，(2008)67-73.

［23］ XU L，DONG B，WANG Y，et al.Electrospinning preparation and room temperature gas sensing properties of porous In2O3nanotubes and nanowires［J］.Sensors and Actuators B，147，(2010)531-538.

［24］ ZHANG Y，YANG J，LI Q，et al.Preparation of Ga2O3nanoribbons and tubes by electrospinning［J］.Journal of Crystal Growth，308，(2007)180-184.

［25］ LIU Z Y，SUN D D，GUO P，et al.An efficient bicomponent TiO2/SnO2nanofiber photocatalyst fabricated by electrospinning with a side-by-side dual spinneret method［J］.Nano letters，7，(2007)1081-1085.

［26］ TAYLOR G.Disintegration of Water Drops in an E-lectric Field［J］.P Roy Soc A-Math Phy，280，(1964)383-397.

［27］ SAVILLE D A，Electrohydrodynamic stability，effect of charge relaxation on the Interface of a liquid jet［J］.Fluid Mech，48，(1971)815-827.

［28］ HARMAN R P A，BRUNNER D J，CAMELOT D M A.Jet break-up in electrohydrodynamic atomization in the cone-jet mode［J］.aerosol Sic，31(1)，(2000)65-95.

［29］ 吴 玥.引入磁场的静电纺丝技术及其对非稳态流动控制机理的研究［D］.上海:东华大学，2007.

Modeling and simulation study of motion locus in electrospinning

DU Hai-ying1，2，WANG Jing1，WANG Juan2
(1.School of Electronic Science and Technology，Dalian University of Technology，Dalian 116023，China; 2.Department of Electromechanical Engineering and Information，Dalian Nationalities University，Dalian 116600，China)

This article took the charged solution with electrical as the study object，the charged solution was simulated as multiple charged particles and which were discretized.Force analysis was applied to single charged particle，molecular dynamics model was built.The movement locus of charged particle was calculated based on runge-kutta method，and simulated using matlab by changing technological parameters of electrospinning，different simulation images have been obtained.The nanofibers were prepared by electrospinning experiment in the same technological parameters，the SEM images of nanofibers were in consisted with simulation images.the results demonstrate that the movement locus of nanofibers is controllable by changing technological parameters during electrospinning.

electrospinning;nanofibers;simulation;molecular dynamics model

TN305 文献标志码:A 文章编号:1005-0299(2012)06-0056-07

2011-11-08.

国家自然科学基金资助项目(No.61176068;No.61131004)，国家科技支撑计划(2009BAH41B05).

杜海英(1978-)，女，在读博士，讲师.

王 兢，E-mail:wangjing@dlut.edu.cn.

(编辑 张积宾)