基于双向渐进结构优化的叶片锻件预成形设计

邵 勇，陆 彬，陈 军，郭平义

(1.上海交通大学模具CAD国家工程研究中心，上海200030; 2.江苏科技大学先进焊接技术省重点实验室，江苏镇江212003)

基于双向渐进结构优化的叶片锻件预成形设计

邵 勇1，2，陆 彬1，陈 军1，郭平义2

(1.上海交通大学模具CAD国家工程研究中心，上海200030; 2.江苏科技大学先进焊接技术省重点实验室，江苏镇江212003)

为了实现体积成形的预成形优化设计，基于双向渐进结构(BESO)优化的思想，提出了一种针对体积成形预成形设计的新方法——拓扑优化法，并详细给出了该方法的优化策略、单元增删准则、插值处理等关键技术.利用自行开发的优化程序，结合DEFORM-2D有限元模拟软件，以理想充填模腔、最小飞边状态为目标，以静水压力的大小作为单元的增删准则，从毛坯的欠填充状态出发，对二维叶片锻件的预成形结构进行了优化设计.优化结果表明:该方法算法原理清晰明确，实现方便，整个过程集成化后，从模拟到优化均可实现自动进行，运行效率高，并具有较高的优化精度.

叶片;体积成形;预成形设计;渐进优化;拓扑优化

对于结构复杂类锻件成形，通常需要多道次变形工步，使毛坯逐渐接近最终锻件形状而成形.预成形工序作为制坯与终锻的过渡，其作用十分关键，特别是对于精密锻造技术，合理的预成形结构更是锻件成形质量的保证.因此，深入研究预成形设计及优化方法，具有重要的现实意义.近年来，随着计算机软硬件的迅速发展和金属塑性成形理论的成熟，基于数值模拟的金属体积成形预成形设计成为了本领域的研究热点，相关的研究成果十分丰富.GAO［1-2］等基于刚粘塑性有限元模拟，采用正反向模拟方法对复杂三维精锻叶片叶身截面进行了预成形设计.但由于尚无通用可靠的脱模准则以及在初始速度场求解方面的困难，因而在一定程度上影响了反向模拟的设计精度和设计效率.基于电场模拟法的复杂锻件预成形设计近期也取得了显著进展［3-4］，但该方法存在初始毛坯确定以及过多人工处理的问题需要解决.基于梯度计算的灵敏度方法是较热门的优化设计方法，Zhao［5］等利用离散的灵敏度分析技术，建立以控制变形力和变形均匀性的多目标函数，对预成形锻件进行了优化设计;而基于连续灵敏度分析技术，Acharjee［6］已在简单的三维锻件预成形优化设计方面做了有益尝试，但灵敏度方程的建立涉及到复杂的数学推导，也不是任意的目标函数都能够与设计变量建立起灵敏度关系，对于复杂的设计模型往往容易陷入局部寻优.

为了避免灵敏度信息的繁琐推导，简化优化问题的实施，一些采用非梯度信息的优化算法得以迅速发展起来，遗传算法就是其中之一.Guan［7］等利用群体规模较小的微观遗传算法，以均匀小晶粒组织为优化目标，建立了热加工过程中动态再结晶、静态再结晶、晶粒长大等机制与晶粒尺度的数学表达式，并对H形锻件的预成形模具进行了优化设计.邹琳［8］采用多种群并行遗传算法，以人工神经网络代替数值模拟预测遗传算法的目标函数值，对挤压模具的几何参数进行了优化设计，但神经网络的模型仍需要较多的有限元模拟来为其提供训练样本，如何提高遗传算法的优化效率仍是值得研究的课题.相对于灵敏度法在设计操作上比较复杂，而遗传算法效率又不高的问题，一种以试验设计为基础，与数理统计相结合，用来处理多变量问题的近似建模方法——响应面法，被应用于预成形优化设计.目前，较常用的构建响应面模型主要有多项式［9］和神经网络［10］两类:多项式模型的响应面设计变量数量不易过多，因而所能处理的几何形状复杂程度有限;而神经网络的响应面方法虽然可以处理的设计变量数量有所增多，预成形形状更加灵活，优化精度也有所提高，但仍然需要足够的样本数据训练神经网络，代价同样是较多的有限元模拟次数.

最近，一种基于拓扑优化的方法——渐进结构优化方法(Evolutionary Structural Optimization，简称ESO)被报道应用于金属塑性预成形优化设计领域［11］.ESO法最初是由Xie等学者提出［12］，其主要思想是基于一定的删除准则，通过有限元数值模拟的结果，逐步将无效或者低效的材料(单元)从模型中删除，使结构最终趋于符合一定工程要求的优化结构.在随后发展的BESO［13］方法里，材料不但能够被删除，还可以被添加到所需要的部位.Lu［14］等首次使用ESO法从坯料的过填充状态出发，对二维叶片叶身截面的预成形结构进行了优化设计，取得了理想的优化效果，但优化过程并没有考虑初始坯料在欠填充状态下的优化效果.本文借鉴了BESO拓扑结构优化的思想，利用C#语言建立了拓扑优化程序，结合DEFORM-2D有限元模拟软件，以理想充填模腔、最小飞边状态为目标，静水压力的大小作为单元的增删准则，从毛坯的欠填充状态出发，对二维叶片锻件的预成形结构进行了优化设计，并与已有文献的优化结果进行了比较.

1 预成形设计的基本理论及方法

1.1 优化目标

预成形优化的首要目标是在保证毛坯完全充满型腔的前提下，锻件飞边尽可能小，因此，目标函数可以用式(1)表示.SD为理想的终锻件体积，属于已知条件输入;Si为第i次迭代成形模拟后，计算出来的锻件实际体积(包括飞边);rmin、rmax为目标函数值Ψ收敛范围的边界值，由设计者按飞边大小相对锻件比率合理设定，应为较小正数.迭代过程中，当满足rmin≤Ψ≤rmax，程序优化结束.本程序充分考虑了初始预成形体积大于或小于理论终锻件体积的不同情况.程序通过判断Si与SD的大小关系，自动调整参数，灵活定制迭代过程中增删单元的数量比率，以达到合理的优化结果，具体的处理方法见单元增删准则部分.另外，为了防止程序因无法收敛而进入无限循环状态，需设置一个最大迭代次数

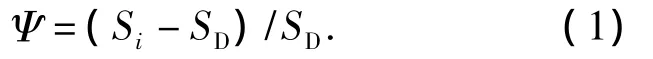
1.2 单元增删准则

金属体积预成形优化与结构拓扑优化的特点并不相同，其主要区别可归结在以下几个方面:①结构优化可以在连续体表面以及内部同时增删单元;而体积预成形优化只能在连续体表面增删单元.②在垂直于外载荷方向上，为避免出现折叠，体积预成形优化后的外形结构要保证外凸性;而结构拓扑优化则无此要求.③优化目标的不同，导致单元增删准则的本质不同.如:结构拓扑优化中通常以Von Mises等效应力作为单元删除准则，但等效应力并不能区分变形体的拉、压应力状态，不利于判断材料变形状态与趋势.在金属充填模腔的过程中，压应力较高通常意味着材料流动困难，往往出现在局部模腔较早即被充满的情况下，该区域就应考虑删除单元;若压应力较低或出现拉应力状态则意味着模腔欠填充，对应着增加单元.因此，以等效应力为单元删除准则就不适用于锻造预成形的优化过程.

单元的增删判据要能够反映材料充填模腔的情况，本文采用静水压力(平均应力)作为单元的增删判据.对于二维平面应变问题，已知一点的应力状态分量有σx、σy、σz、σxy，静水压力计算方法见式(2).如果〉0，则该单元总体处于拉应力状态;而m＜0，则该单元总体处于压应力状态.由于能够真实反映单元个体的应力状态，参照先前提到过的应力状态与单元增删的内在关系，利用静水压力作为单元增删准则是合理的.

金属体积预成形的优化，内部不允许出现孔洞，因此，每次迭代过程中，约束只有实体表面单元可以参与增删操作.在实际的程序处理中，单元并不是真正意义的被增加和删除，而是通过激活与非激活来实现单元的增减，非激活状态的单元无法对预成形外形产生影响，也不参与有限元数值计算.预成形体积要不断增加，因此，每次迭代增加单元的数量要大于删除单元的数量.在程序中非激活单元的数量(Ne)约为表面单元总数的20%;而激活单元的基础数量(Ni)由式(3)决定.

式中:W1为加速因子，合理设置可满足不同尺度优化问题灵活调整增删单元数量比的要求.优化初始，Si远小于SD，激活单元的数量较多，可快速增加预成形体积;随着Si接近SD，激活单元数量也随之下降，预成形体积增加放缓，可较好地实现慢速收敛.

对于体积预成形的优化，只有实体表面单元可以参与激活与否的操作，作为约束条件，激活单元与非激活单元的总和不应超过表面单元的总数量(NS)，其关系见式(4).W2作为比重因子，取值范围为0＜W2＜1，可合理设置以控制参与优化的单元规模.

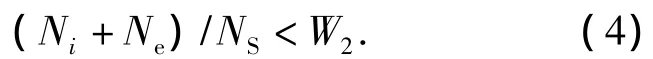
1.3 优化方法

整个优化策略参考图1.首先，基于优化体外形尺寸的大小，确定总体的优化空间并对其进行网格(均布正方形)划分，创建一个背景网格，背景网格应有足够的空间以满足随后所有的预成形优化的形状尺度要求.背景网格空间上的所有单元处于两种状态:激活状态或非激活状态.所有处于激活状态的单元构成了预成形结构.优化程序运行前，需要根据经验确定一个初始预成形形状作为优化原型，并对该原型进行有限元成形模拟.原型模拟以及随后每次迭代过程中的成形模拟结束后，程序都将首先自动分析、处理模拟结果并计算优化目标函数是否满足预设条件，如满足，则迭代终止，优化进程结束，当前预成形结构作为最终优化结果输出;如不满足，则执行拓扑优化程序:①单元场量跟踪:获取单元变形历史，执行数据跟踪操作，使变形前后的单元一一对应，并将计算模拟结果中的静水压力值传递给初始背景网格上的激活单元.②拓扑操作:基于单元增删准则和约束条件判断单元的增删数量以及增删位置，并执行拓扑优化操作，最终得到更新后的拓扑环境下的预成形形状.③曲面轮廓近似:显然，每次拓扑优化后的外形边界都是锯齿状，并不能直接用于有限元模拟分析，需要对外形进行光顺化处理.④有限元模拟:将处理后的预成形几何形状引入有限元系统并重新划分网格、进行下一次迭代成形的有限元模拟.重复上述操作，直至迭代过程结束，得到最终优化后的预成形外形结构.

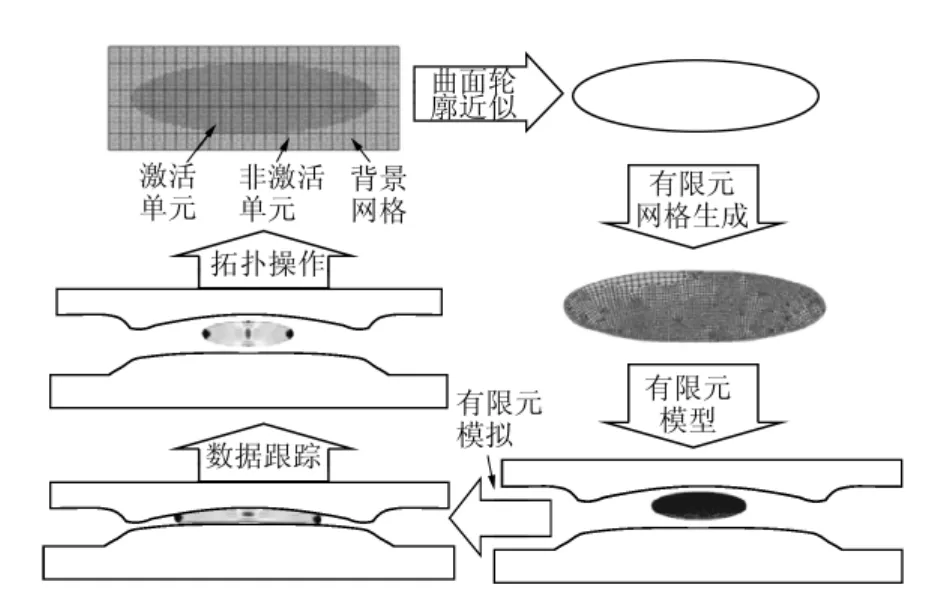
图1 预成形结构优化设计策略

1.4 型面光顺处理

每次迭代优化后的结果使得背景网格上实体表面单元的激活状态不断发生变化，导致整个优化体边缘呈现锯齿状(图2(a))，如果直接用其进行成形模拟分析将影响模拟的精度并有可能导致计算错误，因此，在每次迭代模拟成形过程以前，需自动对拓扑优化后的预成形外表面进行边界光顺处理.具体处理方法是:通过合理提取背景网格上实体表面边界上的节点，利用积累弦长参数化的非均匀B样条曲线构造方法，构造出光滑的表面曲线.再将得到的曲线转换成DEFORM-2D可识别的数据形式导入模拟程序中，并利用DEFORM-2D的自动网格生成程序重新划分网格(图2(b))，进而开始成形过程的有限元模拟.

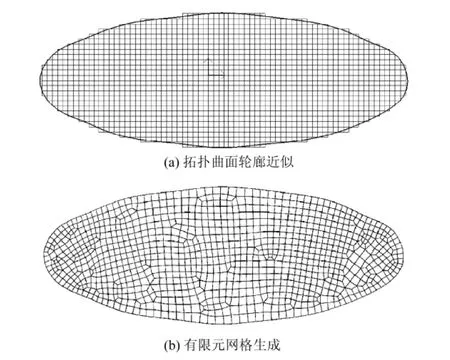
图2 背景网格边界光顺处理

1.5 插值处理

在DEFORM模拟过程中，随着变形程度的增大，坯料原始网格会发生畸变并有可能导致模拟中断，此时程序会自动进行网格重划分，导致网格重划分前后单元编号无法对应.为了获得单元场量(静水压力)的变形历史，需要对网格重划分前后进行插值处理，使最终模拟结果中对应单元上的场量值能够定位到每个初始背景网格上，并以此作为背景网格单元增删操作的判据.插值处理的方法如下.

1)如果没有网格再划分，成形模拟过程中的单元编号以及节点编号就不会发生变化，初始单元节点上的场量值就可以直接通过成形模拟后同编号节点上的场量值直接读取;如果有网格再划分，则不论经过多少次网格重划分的过程，网格节点上的场量值都是累积计算的.因此，只需依次利用网格重划分前后的节点坐标进行插值计算，就可以将最终模拟出来的场量结果逐次传递给初始网格各节点.插值方程见式(5).XQ为网格重划分前待求节点位置上的场量值，Hi为网格重划分后，包容待求节点的四边形单元形函数，XQi为形函数单元每个节点上的场量值.

2)得到有限元初始网格各节点的场量值后，再对背景网格上指定坐标点相对于初始网格进行插值计算.背景网格是均匀分布的正方形单元，以每个单元中心点的静水压力值作为衡量该单元的总体静水压力指标，并以此作为单元增删准则的判据.插值方法采用的是反距离加权插值，插值方程见式(6).为插值点上的静水压力，di为插值点与初始网格节点之间的距离为初始网格节点上的静水压力值.

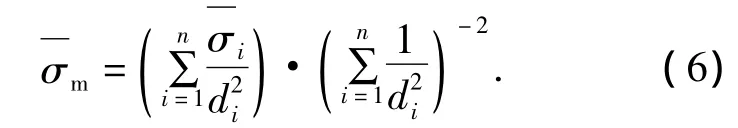
通过上述的插值处理，模拟结果中的静水压力值就可以定位到每个背景网格上.

1.6 特殊约束处理

在每次拓扑优化的迭代过程中，按照增删判据，先进行删除单元操作，再进行增加单元操作.为了避免预成形的实体内部出现空洞，在每次的迭代中，约束只有实体表面的单元能够参与增删操作，且限制已发生删除操作的单元不再参与增加操作.另外，增删单元时，为了避免出现折叠，特殊约束限制使得实体在垂直于加载方向上避免出现内凹.

2 有限元分析模型

叶片材料为镍基合金，最大外廓尺寸约为70 mm×34 mm×34 mm.锻造过程模拟工件采用的是刚粘塑性有限元模型，模具为刚性体设置.叶片初始截面形状为椭圆形，面积约为目标锻件截面积的78%，采用四边形等参单元划分网格.背景网格单元数15 296、节点数15 600.始锻温度1 010℃，模具温度250℃，详细的工件材料本构关系数据如图3所示.锻造过程中的工件与模具传热系数为11 kW/m2·℃、摩擦因子μ=0.3.成形过程中，上模速度为200 mm/s，下模不动，有限元模型如图4所示.

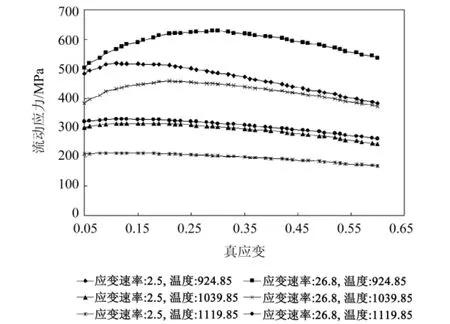
图3 材料的流动应力

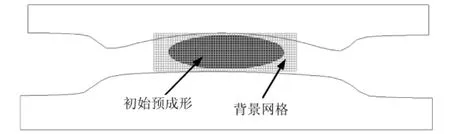
图4 有限元模型

3 模拟结果分析

图5为预成形外形的进化过程以及静水压力分布的有限元模拟结果.随着迭代的进行，预成形的几何形状由最初的椭圆形逐渐转变为哑铃形状，同时坯料体积逐渐增加，经过10次优化后，模腔已完全充满，变形材料流动均匀，取得了理想的成形效果.从所有迭代优化后的静水压力分布来看，锻后截面中间部位均承受较大的三向压应力，并随着毛坯体积的增加，压应力状态也显著增强.过大的三向压应力状态将严重阻碍金属变形，导致材料流动困难，表明此处模腔正处于过填充的状态，从优化策略上对应删除单元;而随着金属向两侧飞边方向的流动，静水压力值逐渐增大，直至料流边缘达到最大值，并呈现出拉应力状态，这表明金属变形较容易，材料在模腔内仍有继续流动空间，从优化策略上则对应增加单元.

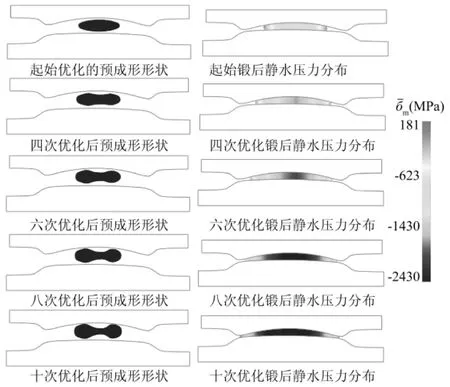
图5 预成形进化过程及静水压力分布

尽管锻后的静水压力分布云图可以近似反映变形前预成形件表面不同部位所对应的静水压力值的大小及分布，但为了更准确地了解单元的具体增删位置，图6直接跟踪了第十次优化的预成形件表面上不同位置的3个节点的变形历史以及对应的静水压力值的变化情况.由于优化后的预成形近似为中心对称结构，因此，图中仅对右半部分进行了分析.由材料流动轨迹上看(图6(a))，P1点几乎没有位移、P2点有少量位移、P3点位移最大，这表明成形过程中，叶片截面两侧部分型腔主要由P2至P3部分的金属流动填充，而中心部位变形很小.从静水压力值变化来看(图6(b))，P3点在整个成形过程中，一直处于100 MPa左右的拉应力状态，表明该区域金属持续发生流动变形，参考单元的增删判据，此处在迭代过程中将不断增加单元.在成形阶段中前期，由于截面中心部位有足够的自由空间，P1至P2之间的变形区域无法形成三向压应力，因而表现出较低的压应力波动状态(-500～0 MPa)，而P2点的压应力状态要明显强于P1点，其原因在于P2区域除了受相邻金属的约束外，还受模腔约束，因而压应力更显著;当成形进入后期，特别是中心区域充满后，P1至P2之间的材料区域进入了三向压应力状态，表现为静水压力值的快速下降，相比P2区域，P1处金属流动则更加困难，因此，成为了整个预成形截面上压应力最大的区域，因而在迭代过程中将持续的删减单元，并最终促成了预成形的哑铃结构.

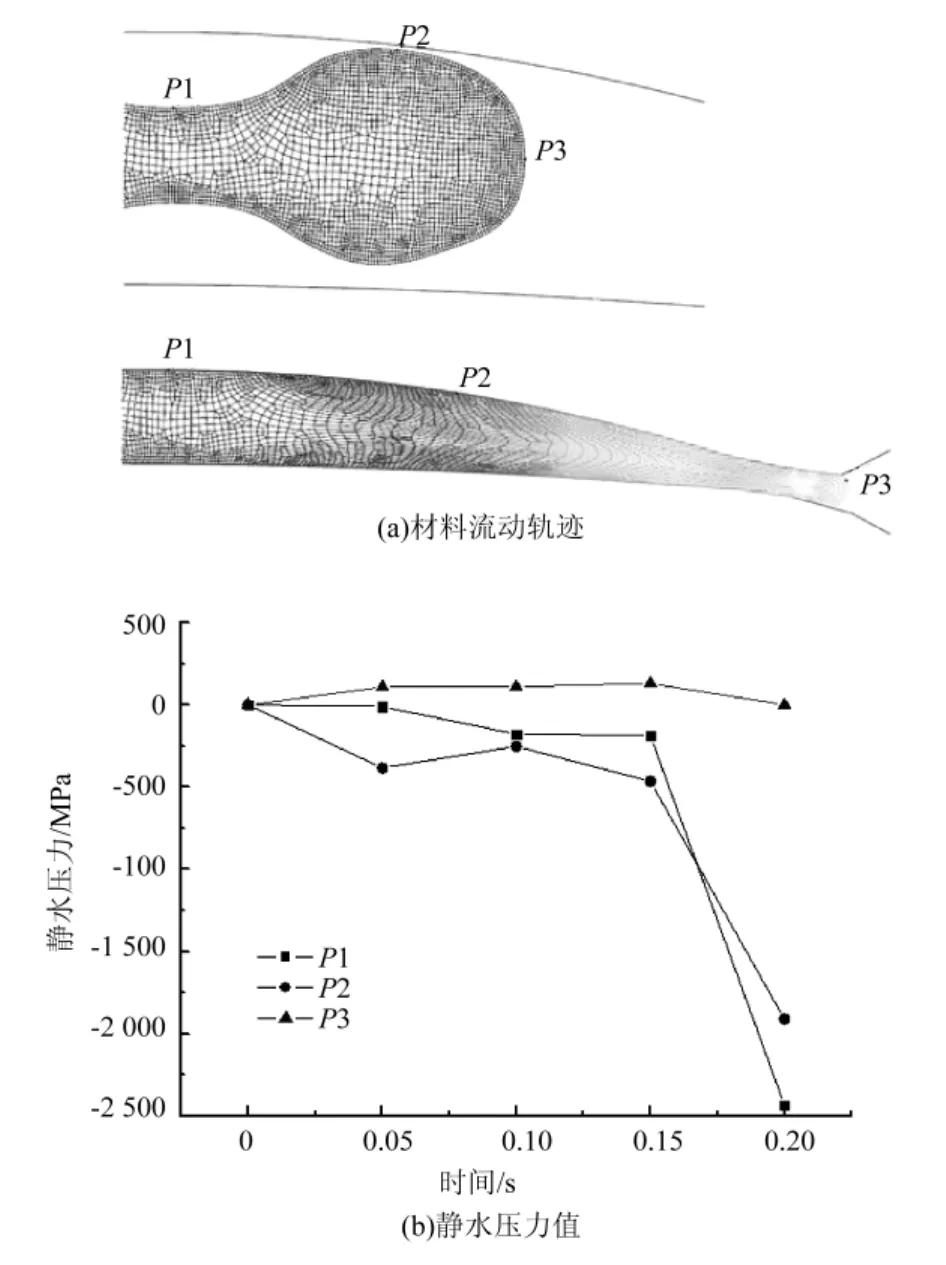
图6 十次迭代优化的预成形表面节点变形历史及对应的静水压力值

图7给出了传统工程叶片叶身预成形设计结构(椭圆形)与十次优化后预成形结构在锻后的等效应变比较.由图7可见，总体上应变较大的区域主要集中在叶片锻件的进排气边缘:未优化状态下的预成形由于初始坯料体积较大，材料变形流动剧烈，造成了该区域异常高的应变;而经十次优化的预成形锻后在该区域的等效应变则明显减小.从图8的等效应变数值统计来看，最大最小单元等效应变差由传统预成形设计状态下的约1.948减少至十次优化时的1.486，表明预成形结构的优化使得单元等效应变在波动范围上显著减小;单元平均等效应变由1.18减少至0.833，表明单元总体的等效应变量也明显减小;而单元等效应变偏差由0.382减小至0.370，说明变形体内各单元之间的等效应变偏差量在减小，单元等效应变的趋同性得到提高.单元等效应变偏差和单元平均等效应变的计算方法见式(7)和式(8).通过以上分析可以得出，渐进优化的预成形结构有效地改善了锻件在成形过程中的变形均匀性、减小了单元总体变形量，对最终锻件的组织及性能有积极的影响.

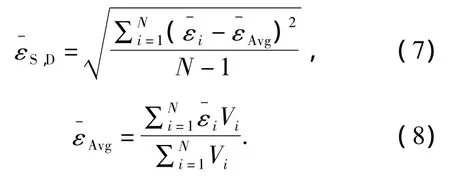
图7 传统叶片预成形与十次优化后预成形锻后的等效应变比较

图9给出的是目标函数值随优化迭代进程的变化情况.可以看到，Ψ值从初始欠充满状态下的-0.216，到第十次迭代终止时略微过充满状态的0.008，中间Ψ值的变化比较均匀，表明算法在优化过程中运行有效、稳定.相比于文献［14］中的优化结果，本文所优化的预成形哑铃结构的两端相对较大，其主要原因在于:虽然哑铃的两端都在增加单元，但增加的幅度是不一样的.本文从欠填充状态出发，优化过程增加单元的数量要大于减少单元的数量;而文献［14］则正好相反.增加单元绝对数量上的差异造成了预成形几何结构上的差异，但两优化结构的总体趋势是一致的.由此证明，不论初始毛坯体积状态如何，基于双向渐进结构的预成形优化设计均可给出理想的、可靠的优化结果.

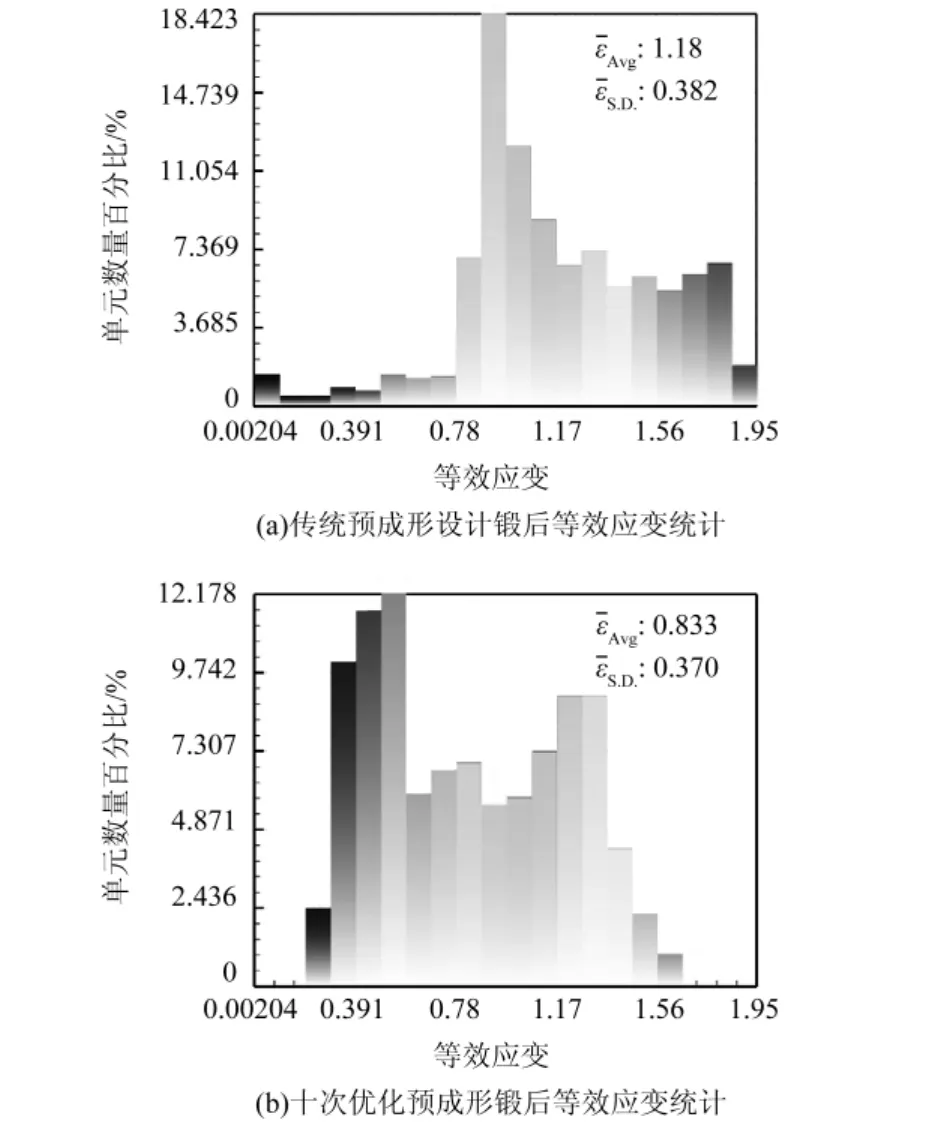
图8 传统叶片预成形与十次优化后预成形锻后的等效应变的数值统计

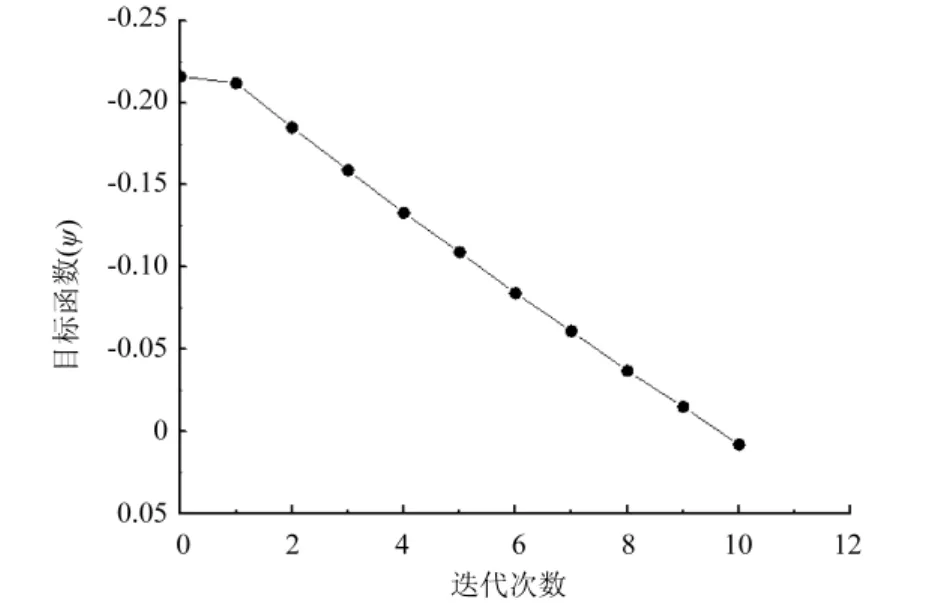
图9 迭代次数与对应的目标函数值

4 结论

本文采用了BESO算法，以静水压力为单元增删判据，以理想填充为目标函数，对二维叶片截面的预成形几何外形进行了优化设计.模拟及优化结果表明:

1)优化后的预成形结构在完全充满模腔的同时，获得了较小、均匀的飞边;成形过程中，变形材料流动均匀、在降低高应变区域变形程度的同时坯料整体的变形均匀性明显提高，预成形结构的优化设计效果比较理想.

2)从毛坯的欠填充状态出发完成了预成形优化过程，验证了算法的稳定性与可靠性.相比于其他预成形优化算法，拓扑优化算法有着较高的优化精度与优化效率，特别适用在其他方法难以求解时，可以方便地得到较好的优化结果.

3)背景网格尺度对优化过程及结果有重要影响，过少的网格将影响优化精度，而过多的网格则导致计算量的增加，因此，合适的网格规模显得十分重要.

［1］ GAO T，YANG H，LIU Y L.Backward tracing simulation of precision forging process for blade based on 3D FEM［J］.Transactions of Nonferrous Metals Society of China，2006，16(2):639-644.

［2］ GAOT，YANG H，LIU Y L.Influence of dynamic boundary conditions on preform design for deformation uniformity in backward simulation［J］.J Mater Proc Technol，2008，197(1/2/3):255-260.

［3］ CAI J，LI F G，LIU T Y.A new approach of preform design based on 3D electrostatic field simulation and geometric transformation［J］.Int J Adv Manuf Technol，2011，56(5/6/7/8):579-588.

［4］ CAI J，LI F G，LIU T Y.Preform design for large-sized frame forging of Ti-Alloy based on 3-D electrostatic field simulation and geometric transformation［J］.J Mater Eng P，2010，20(9):1491-1496.

［5］ ZHAO X H，ZHAO G Q，WANG G C，et al.Sensitivity Analysis Based Multiple Objective Preform Die Shape Optimal Design in Metal Forging［J］.J Mater Sci Technol，2006，22(2):273-278.

［6］ ACHARJEE S，ZABARAS N.The continuum sensitivity method for the computational design of three-dimensional deformation processes［J］.Comput Methods Appl Mech Engrg，2006，195(48/49):6822-6842.

［7］ GUAN J，WANG G C，GUO T，et al.The microstructure optimization of H-shape forgings based on preforming die design［J］.Materials Science and Engineering A，2009，499(1/2):304-308.

［8］ 邹 琳.遗传算法的挤压模具多目标优化设计与研究［D］.武汉:华中科技大学博士论文，2004.ZOU Lin.Multi-objects optimization design of extrusion-die system using genetic algorithms［D］.Wuhan: Huazhong University of Science and Technology，2004.

［9］ YANG Y H，LIU D，HE Z Y，et al.Optimization of preform shapes by RSM and FEM to improve deformation homogeneity in aerospace forgings［J］.Chinese Journal of Aeronautics，2010，23(2):260-267.

［10］ TANG Y C，ZHOU X H，CHEN J.Preform tool shape optimization and redesign based on neural network response surface methodology［J］.Finite El A，2008，44 (8):462-471.

［11］ NACEUR H，GUO Y Q，BATOZ J L.Blank optimization in sheet metal forming using an evolutionary algorithm［J］.J Mater Proc Technol，2004，151(1/2/3): 183-191.

［12］ XIE Y，STEVEN G.A simple evolutionary procedure for structural optimization［J］.Computers and Structures，1993，49(5):885-896.

［13］ QUERIN O M，STEVEN G P，XIE Y M.Evolutionary structural optimization(ESO)using a bi-directional algorithm［J］.Engineering Computations，1998，15 (8):1034-1048.

［14］ LU B，OU H，CUI Z S.Shape optimisation of preform design for precision close-die forging［J］.Struct Multidisc Optim，2011，44(6):1-12.

Optimal design of preform of blade forging based on Bi-directional evolutionary structural optimization

SHAO Yong1，2，LU Bin1，CHEN Jun1，GUO Ping-yi2
(1.National Die and Mold CAD Engineering Research Center，Shanghai Jiao Tong University，Shanghai 200030，China; 2.Jiangsu Provincial Key Laboratory of Advanced Welding Technology，Jiangsu University of Science and Technology，Zhenjiang 212003，China)

Based on the Bi-directional evolutionary structural optimization(BESO)，a new topology optimization method is proposed and adopted for preform optimization design of bulk metal forming，and the key technologies of topology optimization in detail such as optimal strategy，element removal and addition criteria，interpolation technology，etc are given.By utilizing the self-programmed code and deform-2D FE software，an blade preform optimal case，of which the objective is sufficient filling of die cavity and flash minimization，element removal and addition criteria is hydrostatic stress and initial blank state is insufficient filling，is implemented and evaluated.The result shows that the developed method is explicit in principle and simple to be carried out，it has high operating efficiency and optimal accuracy and can run automatically once be integrated in program code.

blade;bulk metal forming;preform design;evolutionary structural optimization;topology optimization

TG312 文献标志码:A 文章编号:1005-0299(2012)06-0108-07

2012-05-09.

国家自然科学基金资助项目(51005150).

邵 勇(1978-)，男，博士研究生，讲师;

陈 军(1969-)，男，教授，博士生导师.

陆 彬，E-mail:binlu@sjtu.edu.cn.

(编辑 吕雪梅)