基于模糊综合评价法的大学文科生数学感知程度评价的研究*

余桂东，伍代勇

(安庆师范学院数学与计算科学学院，安徽安庆 246133）

基于模糊综合评价法的大学文科生数学感知程度评价的研究*

余桂东，伍代勇

(安庆师范学院数学与计算科学学院，安徽安庆 246133）

以大学文科生对数学感知情况的问卷调查为基础，采用模糊综合评价法建立了大学文科生对数学感知情况的评估指标体系和评价方法.首先确定了评估指标体系中各指标的权重，然后建立评价集并构造了模糊评价矩阵，最后模糊合成得到了评价结果.评价结果表明大学文科生对数学的感知情况较好，对数学学习的兴趣程度也较高.根据评价结果提出了大学文科生数学课程的如下建议:一是增加课程的趣味性，穿插一些与文科生相关的数学的小故事;二是多训练学生的逻辑思维和创造性思维，注重教授给学生归纳、类比等数学方法和极限、抽象归纳、规划等数学思想;三是拓宽学生的视野，让学生们了解数学在各个领域内的应用.

模糊综合评价法;大学文科生;数学感知;评价

人类历史的发展无处不证明数学所起的巨大作用.随着现代科学技术的飞速发展，数学对科技的发展起着重要的推动作用，不仅自然科学和工程技术工作者离不开数学，现代的人文社会科学工作者也必需掌握一些高等数学知识.马克思说过:“一门科学，只有当它成功地应用了数学的时候，才能达到真正完善的地步”这说明在高等教育面前，人人需要学数学，我们大学文科专业的学生也不例外，但最近华中科技大学新闻专业学生，写信给校长说文科生学数学无用的话题引起了社会广泛关注，也引起了我们数学教育者的深思——我们的大学文科生对数学感知程度到底怎样?我们应该在大学文科专业开设怎样的数学课程?因此我们对大学文科专业的学生进行了广泛问卷调查，并选取了18个问题作为评价指标，利用模糊综合评价法［1～2］得出大学文科生对数学感知程度，并根据结果给出开设大学文科生数学课程的若干建议.

1 评估指标体系的构建及指标权重

1.1 评估指标体系的构建

建立科学合理的评估指标体系是做好高校文科生对数学的感知情况评价的基础和关键.为了抓住影响文科生对数学的感知情况的主要因素，筛选出具有代表性和高度概括性的主导指标，本研究前期进行了大量问卷调查，并将调查对象归为不同专业、年级和性别，最终提取确定出影响数学感知情况的指标集.

1.2 确定指标集

指标集为各种指标的集合，共划分为两级指标集:一级指标集与二级指标集.一级指标如下:

U={对数学的概念理解U1，对数学思想与方法的感知U2，对数学应用的感知U3，对数学的兴趣程度U4}.

二级指标如下:

U1={数学属于哪种学科U11，数学的特点U12，数学课程U13，数学的目的U14，学习数学的意义U15}，

U2={文科数学应该主要介绍哪些方面的知识U21，自己了解的数学方法U22，自己了解的数学思想U23，自己专业需要的数学思想与方法U24}，

U3={数学在商品销售中的应用U31，数学在风险投资中的应用U32，数学知识与自己所学专业的关系U33，数学知识对自己未来走上社会的帮助U34}，

U4={自己喜欢的数学课上课形式U41，一周花多长时间看数学U42，平时看哪类数学书U43，知道哪些数学家的名字U44，自己喜欢的数学课的类型U45}.

1.3 建立权重集

在确定一级指标的权重时采用了专家问卷调查法［3］，针对研究文科数学的专家(教授)，共发放问卷30份，回收28份.每份专家问卷都对文科生对数学感知情况的一级指标和二级指标打分，根据层次分析法对所有专家评价结果进行汇总计算得到权重(见表1).

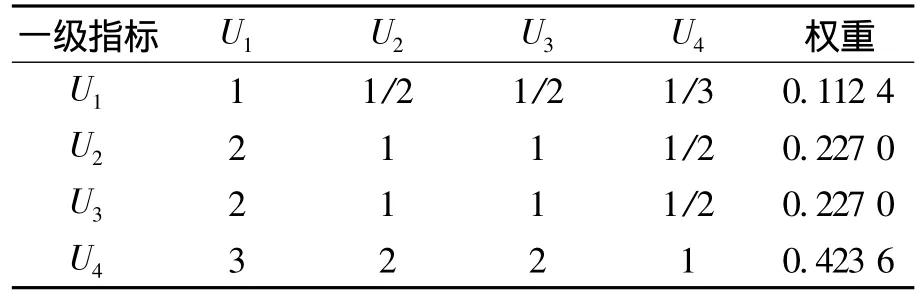
表1 一级指标判断矩阵及权重

其判别矩阵最大特征值为lmax=4.010 4，令n为一级指标个数，则一致性指标为C.I=(lmax－n)/(n－1)=(4.010 4 －4)/(4 －1)=0.003 5，随机一致性指标为R.I=0.887 9，一致性比率为 C.R.=C.I/R.I=0.003 9≤0.10，所以一级指标具有较好的一致性，计算出的指标权重是有意义的，同理可得到二级指标中各一级指标下的相对权重(见表2).

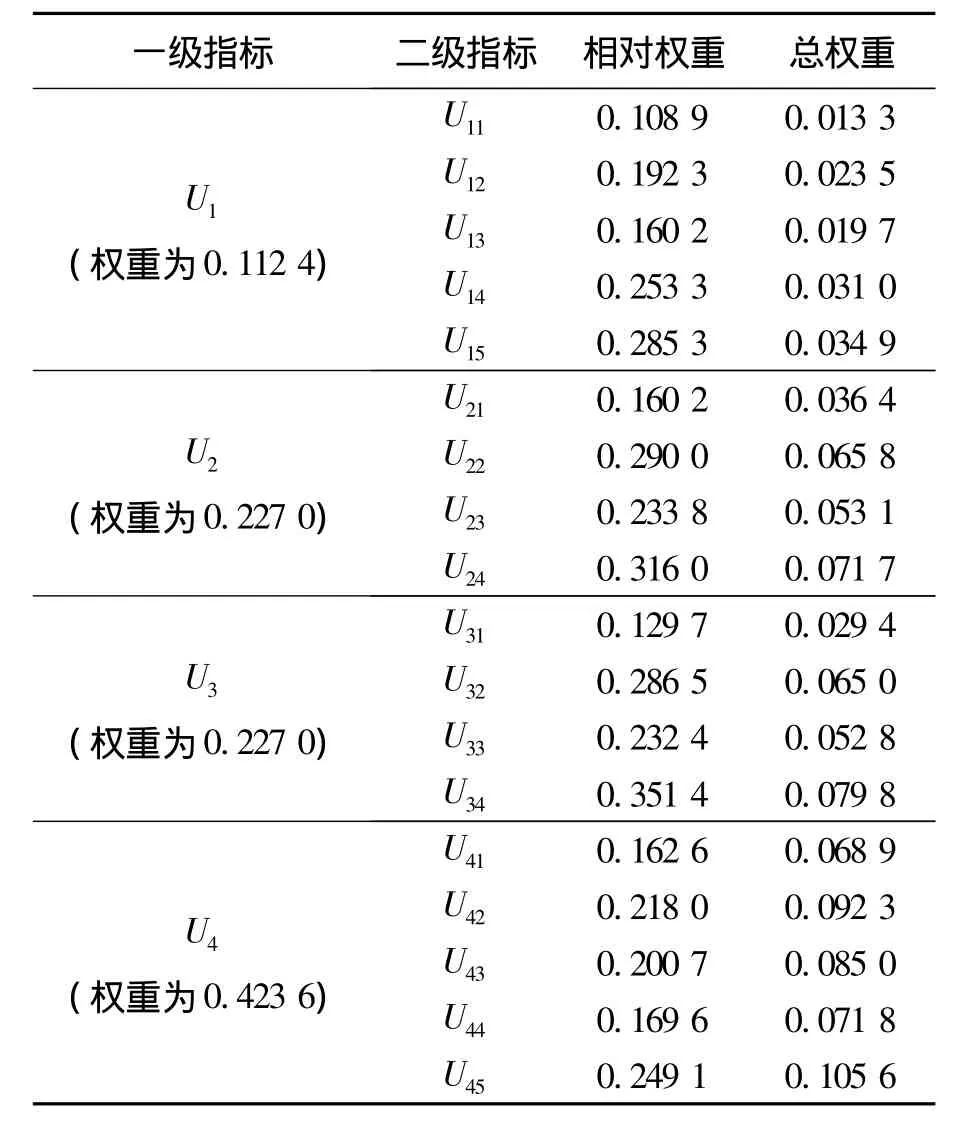
表2 文科生对数学感知情况评估指标体系定量化

2 评价集和模糊评价矩阵的建立

将文科学生对数学感知认识的程度划分为四个等级，即评价集为V={深，较深，一般，浅}.

在建立各级评价指标权重以及评价集的基础上，接下来建立模糊评价矩阵［4～5］.首先选择评价人员，若有n个人员进行评价，当对第Uij项指标进行评判时有mijp个评价者选择p等级，则所有评价者对数学感知认识的程度在Uij方面评价为p等级的频率为rijp=mijp/n.由此可到对Uij指标评价结果的行矩阵

将所有二级指标评价结果的行矩阵排列起来就得到评价指标模糊矩阵表:

本研究以安庆师范学院文科生为对象，共发放正式问卷120份，收回有效问卷114份，根据分析得出问卷的信度和效度都符合研究要求，并得到其模糊评价矩阵(见表3).

3 模糊合成及结果分析

模糊合成公式为:

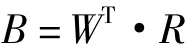
式中:WT为指标总权重行向量;R为模糊评价矩阵.

由上式计算得:B=WT·R=(b1，b2，b3，b4)=(0.237 7，0.309 3，0.266 4，0.186 6).因此有23.77% 大学文科生认为对数学的感知程度深，30.93%认为较深，26.64%认为一般，18.66%认为浅.按照最大隶属原则，最大数字b2=30.93%对应的级别为较深，即大学文科生对数学的感知程度为较深.这说明总体来讲，大学文科生对数学的感知情况还是挺好的，对数学学习的兴趣程度也较高.故在大学文科专业开设高等数学课程，有它的实际基础与需求空间.根据调查结果，我们可以针对大学生的爱好，增加高等数学课程的趣味性［6］，让老师们上课的风格趋于幽默化、生动化，在课堂上经常穿插一些关于数学的小故事，另外，多训练学生的逻辑思维和创造性思维，注重教授给学生归纳、类比等数学方法和极限、抽象归纳、规划等数学思想，拓宽学生的视野，让学生们了解数学在各个领域内的应用，这样一定能使文科专业高等数学课程成为一门趣味性浓、实用性强、学生非常热爱的一门课程.

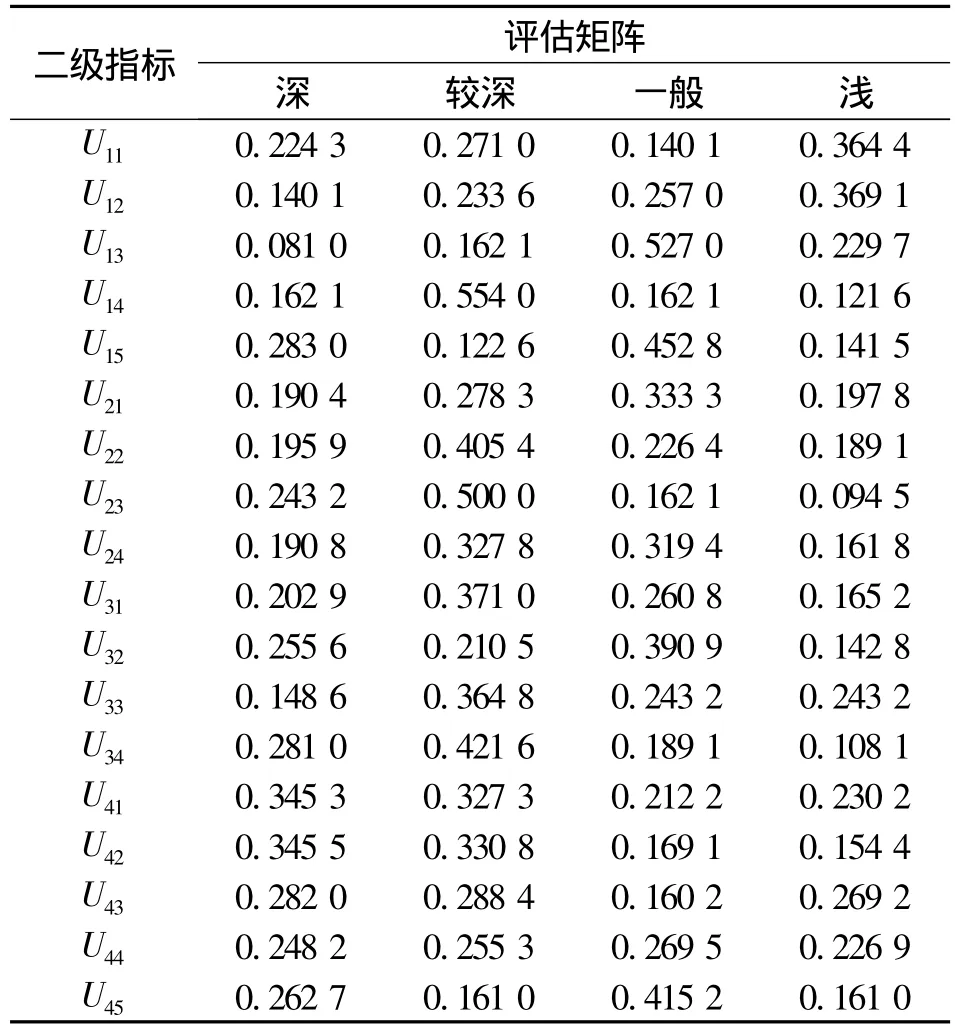
表3 模糊评价矩阵表

［1］刘鹏超，张喜刚.AHP－模糊综合评判法在高校科研实验室评估中的作用［J］.中国电力教育，2011，(10):134－135.

［2］罗曙霞，王化麟，苗永春.AHP－模糊综合评判法在项目后评价中的应用［J］.现代商业，2011，(14):158－159.

［3］王涛.模糊综合评判在高校排课系统评价中的应用［J］.大学数学，2006，22(2):5－10.

［4］王秋萍，苏哲斌.多级模糊综合评判在高校教师考评中的应用［J］.数学的实践与认识，2008，38(8):204－206.

［5］王亚君，张玉智，栾加双.基于模糊综合评价的企业人才流失影响因素分析［J］.工业技术经济，2009，28(10)118－120.

［6］唐小丹.大学文科生数学学习观调查研究［J］.贵州民族学院学报，2006，(6):196 －198.

The Study on Evaluation of Mathematic Perception Degree of College Liberal Arts Based on Fuzzy Comprehensive Evaluation Method

YU Gui－dong，WU Dai－yong

(School of Mathematics ＆ Computation Sciences，Anqing Normal College，Anqing Anhui 246133，China)

According to the questionnaires on mathematic perception situation of college liberal arts students，it establishes the evaluation index system and evaluation methods of mathematic perception situation of college liberal arts students with fuzzy comprehensive evaluation method.Firstly，it determines the weight of each index in the evaluation index system，and then it creates the evaluation set and constructs the fuzzy evaluation matrix，at last it gets the evaluation results by fuzzy synthetic.The evaluation results show that college liberal arts students have better mathematic perception situation and have higher degree of interest in mathematic learning.According to the evaluation results，it gives the following recommendations about mathematic curriculum of college liberal arts students:the first is to increase the fun of the course，insert mathematic stories related to liberal arts students;the second is to give more training on students’logical thinking and creative thinking，pay attention to teach students induction，analogy and other mathematic methods and limit，abstract induction，planning and other mathematic thinking;the third is to broaden students’horizons，so that students understand the application of mathematics in various fields.

fuzzy comprehensive evaluation method;college liberal arts students;mathematic perception;evaluation

O 159

A

1673－2103(2012)02－0112－03

2012－03－31

安徽省重点教学研究项目(20100675)

余桂东(1973－)，女，安徽潜山人，副教授，在读博士研究生，研究方向:基础数学.