图论在大学生数学建模竞赛中的应用*

王国兴

(兰州商学院信息工程学院，甘肃兰州 730020）

图论在大学生数学建模竞赛中的应用*

王国兴

(兰州商学院信息工程学院，甘肃兰州 730020）

随着图论的发展，图论的理论和方法广泛应用于大学生数学建模竞赛中.讨论了大学生数学建模竞赛中如下图论问题的应用:二分图的最大匹配，最大点独立集;最佳推销员回路，哈密尔顿图;最小生成树等.

图论;二分图;最佳推销员回路;哈密尔顿图;最小生成树;大学生;数学建模竞赛

图论是数学的一个重要分支，它广泛地应用于物理学、现代控制论、信息论、管理科学、计算机技术等诸多领域.对于自然科学、工程技术、经济管理和社会现象等诸多方面的问题，利用图论的理论和方法能够提供有力的数学模型使问题得到解决.在国内外大学生数学建模竞赛中，与图论的知识和方法有关的问题已出现多次.这里有针对性地讨论图论在大学生数学建模竞赛中的应用.

图的基本概念如下［1～2］.

一个图G是指一个有序三元组(V(G))，E(G)，φG)，其中V(G)是非空的顶点集，E(G)是不与V(G)相交的边集，而φG是关联函数，它使G的每条边对应于G的无序顶点对.若e是一条边，而u和v是使得φG(e)=uv的顶点，则称e连接u和v;顶点u和v称为e的端点.

图G中与顶点v关联的边的数目，称为v(在G中)的度，记作dG(v).

图G中的顶点数用符号v(G)或|v(G)|表示，边数用符号ε(G)表示.

1 二分图的最大匹配、最大点独立集在大学生数学建模竞赛中的应用

定义1 若V(G)=X∪Y，X∩Y=φ，X、Y均非空，且图G的每一条边都有一个顶点在Y中，则称图G为二分图.

定义2 图G的互不相邻的顶点子集称为点独立集.

问题1 某锁具厂生产一批弹子锁具，每个锁具的钥匙有个5槽，每个槽的高度从(1，2，3，4，5，6)6个数(单位略)中任取一个，由于工艺及其它原因，制造锁具时对5个槽的高度还有两个限制:至少有三个不同的数;相邻两槽的高度之差不能是5.满足以上条件的所有互不相同的锁具称为一批.另外，若两个锁具对应的5个槽高中有4个相同，另一个槽高只相差1，则可能互开;其它情形不可能互开.现在的问题是:一批锁具有多少个?若60个装一箱，团体购买多少箱不会出现互开现象?

分析 6种高度5个槽的钥匙最多可能有65=777 6，通过排列组合，除去不满足条件的各种情况，可以算出一批锁具的总数为5 880件.

由于两个锁具对应的5个槽高中有4个相同，另一个只相差1，被视为互开，那么它们各自槽高之和必为一个奇数、一个偶数.另外，槽高之和为奇数和偶数的锁具可以一一对应，因而各占一半:2 940件，槽高之和为奇数(或偶数)的两锁具之间不可能互开，所以若60个装一箱，2 940个锁具可以装49箱，49箱槽高之和为奇数或偶数的锁具，肯定不能互开.现在的问题是49箱是不是最大可能的?

建立模型 将锁具的互开关系用图表示，锁具集合用V=V1∪V2表示，其中V1和V2分别表示槽高之和为奇数和偶数的锁具集合.若vi∈V1，vj∈V2能够互开，则两点连一边.这样构成一个二分图G=(V1∪V2，E)，V1和V2都是点独立集，因为它们内部的点互不相邻.为了说明它们都是最大的独立集，引入点覆盖的概念.图G的顶点子集K称为一个点覆盖，如果图G的每一条边，至少有一个顶点包含在K里.点独立集与点覆盖有互补的关系［3～4］.

设α(G)，β(G)分别表示图G的最大点独立集所含点数，最小点覆盖所含点数，简记为点独立数和点覆盖数.由上面的讨论有:

定理1 α(G)+β(G)=|V(G)|.

类似地给出边独立集(匹配)和边覆盖的概念与关系.图G的边子集E1称为边覆盖，如果图G的任何一个顶点至少是E1当中一条边的顶点.设α'(G)、β'(G)分别表示图G的最大匹配所含边数、最小边覆盖所含边数，简记为边独立数和边覆盖数.它们之间有如下数量关系:

定理2 若图G没有孤立顶点，即顶点的最小度δ＞0，则α'(G)+β'(G)=|V(G)|.

对于任何的匹配M和任何的点覆盖K，因为K至少要覆盖M当中的每一条边，所以|M|≤|K|，当然最大匹配与最小点覆盖之间也有关系，α'(G)≤β'(G).特别地:

定理3 对于二分图G，有α'(G)=β(G).

推论1 对于二分图G，如果顶点的最小度δ＞0，则α(G)=β'(G).

引理1 二分图G=(V1∪V2，E)存在饱和V1的每个顶点的匹配⇔对所有S⊆V1，有|NG(S)|≥S.其中NG(S)表示S在图G中的邻点集合.

模型求解 对问题1构造的二分图，由于奇数类锁具与偶数类锁具的对称性，引理1满足，所以存在饱和V1的每个顶点的匹配M，而V1的顶点互不相邻，因此2 940=|V1|≤|M|≤α'(G)=β(G)=|V|－α(G)，从而点独立数α(G)≤|V|－2 940=2 940.由于奇数类点独立集和偶数类点独立集都有2 940个点，所以α(G)=2 940，说明奇数类点集和偶数类点集都是最大的点独立集，因此49箱是不能互开的最大可能.

2 哈密尔顿图、最佳推销员回路在大学生数学建模竞赛中的应用

定义3 经过图G的每个顶点正好一次的圈，称为图G的哈密尔顿圈，简称H圈.

定义4 在加权图G=(V，E)中，1)权最小的哈密尔顿圈称为最佳H圈;2)经过每个顶点至少一次且权最小的闭通路称为最佳推销员回路.

问题2 1998年全国大学生数学建模竞赛B题:灾情巡视路线问题.题目给出了某县的乡(镇)、村公路网示意图，今年夏天该县遭受水灾.为考察灾情、组织自救，县领导带领有关部门负责人到全县各乡(镇)、村巡视.巡视路线指从县政府出发，走遍各乡(镇)、村，最后回到县政府的路线.问题是:若分三组巡视，试设计总路程最短且各组尽可能均衡的巡视路线.

分析 灾情巡视路线问题是一个寻求最佳推销员回路的问题.最佳推销员回路的问题可转化为最佳H圈的问题.

建立模型 求最佳推销员回路的方法是由给定的图G=(V，E)构造一个以V为顶点集的完备图G'=(V，E')，E'中每条边(x，y)的权等于顶点 x与 y在图 G 中最短路径的权，即∀(x，y)∈E'，ω(x，y)=mindG(x，y).

在图论中有以下定理［1～2］:

定理4 加权图G的最佳推销员回路的权和G'的最佳H圈的权相同.

定理5 在加权完备图中求最佳H圈的问题是NP——完全问题.

定理6 G是v(G)≥3的图，且∀u，v∈V(G)，dG(u)+dG(v)≥v(G)，则G中有哈密尔顿圈.

模型求解 下面给出求加权图G=(V，E)的最佳推销员回路的近似算法:

1)用图论软件包求出G中任意两个顶点间的最短路，构造出完备图G'=(V，E')，∀(x，y)∈E'，ω(x，y)=mindG(x，y);

2)输入图G'的一个初始H圈;

3)用对角线完全算法产生一个初始H圈;

4)随机搜索出G'中若干个H圈;

5)对2)、3)、4)步所得每个H圈，用二边逐次修正法进行优化，得到近似最佳H圈;

6)在5)求出的所有H圈中，找出权最小的一个，此即要找的最佳H圈的近似解.

然后用这个方法求解得出问题的解.

再看一个简单问题:

问题3 围圆桌至少有5人相聚，怎样调整他们的座位，使得每个人两侧出现新的邻座.

求解 若恰好5人，设原来座次为ABCDEA，可调整为ADBECA.若超过5人，则以人为顶点，仅当两人原来不相邻座时，在此相应的两顶点间连一边，得一图G，由于每个顶点的度都是|V(G)|－3，于是任意两顶点度之和为2v(G)－6，又v(G)＞5，故2v(G)－6≥v(G)，由定理6，G是哈密尔顿图，可按哈密尔顿圈上的次序重新入席，即得到每个人有两个新的邻座.

3 最小生成树在大学生数学建模竞赛中的应用

问题4 有一石油公司计划为它拥有的许多存储站设计一个管道连接系统，它共有9个存储站，如果两个存储站之间可以修管道，就用一条边连接起来，用一个数表示修这两站之间的管道所需的费用，这样这个公司所有的存储站和可能修管道的情况，如图1表示.

图1 石油公司所有的存储站和可能修管道的情况

设计计划要求:管道网可以把任意两个存储站都连接起来，且修管道的费用最低.

分析 从图论的角度来说，图1是一个连通图，每一个边都被赋予了一个数，称之为赋权图.问题是确定出另一个连通图，其顶点集与原图的顶点集一样，仅保留原图中的一部分边，把这一确定的新图称作原图的生成子图，并且使子图的所有边的权之和最小.

建立模型 要找的子图必须是连通的，直观地说子图具有的边应尽量地少，即这个子图不能含有任何回路，因为去掉回路中的任何边都不会影响它的连通性质，我们把不包含回路的生成子图称为原图的生成树.不含回路的连通图，又称树.

树图中的顶点有两类，一类是度为1的顶点，称为悬挂点，另一类是度大于1的顶点，称为割点.一旦去掉割点及与之相连的边，图就不连通了.

容易得出以下结论:

定理7 一个具有n个顶点的连通图，1)连通子图是生成树的充要条件为它具有n－1条边;2)子图是生成树的充要条件为它有n－1条边且无回路.

现在的问题变成了求权重最小的生成树了，简称为最小生成树.下面给出一个求最小生成树的算法:

第一步:我们把所有的边按其权重从小到大排列起来;

第二步:先选定第一条边;

第三步:边序列中选择下一条边的原则是此边与前面的边全在一起不构成回路;

第四步:直到选出n－1条边.

模型求解 通过上述方法得到了一个生成树，关于它一定是最小生成树的证明这里省略.这个算法是1956年由Kruskal提出的又称作Kruskal算法.由于在不出现回路的前提下取权小的边，故又称作“贪婪算法”.下面用Kruskal算法讨论问题4.

第一步:我们按权重从小到大把边排列为:

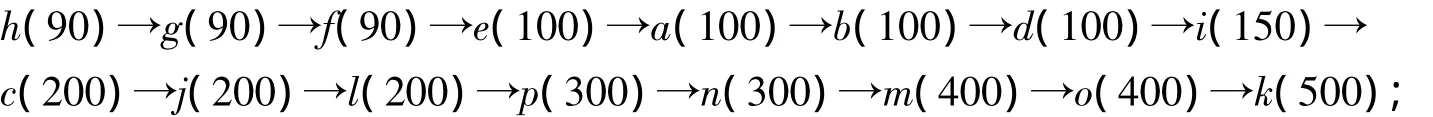
第二步:确定h为第一条边;

第三步:h(90)→g(90)→f(90)→e(100)→a(100)→b(100)→d(100)→i(150);

第四步:上面八条边组成了最小生成树.

除了以上的应用，很多图论理论和方法在大学生数学建模竞赛中都有广泛应用.如欧拉图、染色、最短路等.最后列出历年大学生数学建模竞赛中能用图论理论和方法求解的问题.

1993年B题:足球队排名;1994年A题:逢山开路;1994年B题:锁具装箱问题;1995年B题:天车与冶炼炉的作业调度;1997年B题:截断切割的最优化排列;1998年B题:灾情巡视的最佳路线;1999年B题:钻井布局;2004年A题:奥运会临时超市网点设计;2007年B题:乘公交，看奥运;2011年B题:交巡警服务平台的设置与调度.

［1］Bondy J A，Murty U S R.Graph Theory with Applications［M］.New York:The Macmillan Press Ltd，1976.

［2］王朝瑞.图论［M］.北京:北京理工大学出版社，2000.

［3］边馥萍，侯文华，梁冯珍.数学模型方法与算法［M］.北京:高等教育出版社，2005.

［4］叶其孝.大学生数学建模竞赛辅助教材(二)［M］.长沙:湖南教育出版社，1997.

The Usage of Graph Theory in the Mathematical Modelling Contest

WANG Guo－xing

(School of Information Engineering，Lanzhou University of Finance and Economics，Lanzhou Gansu 730020，China)

With the development of the graph theory，its theories and methods are widely used in the Mathematical Modelling Contest.The discussion about the application of graphic problems in the Mathematical Modelling Contest:maximum matching of bipartite graph，maximum independent set;optimal travelling salesman loop，Hamilton graph;Solve Minimum Spanning Tree and so on.

graph theory;bipartite graph;optimal travelling salesman loop;Hamilton graph;Solve Minimum Spanning Tree(SMST);college student;the Mathematical Modelling Contest

O 157.6

A

1673－2103(2012)02－0108－04

2012－04－08

国家自然科学基金资助项目(61163037，61163054);兰州商学院科研资助项目(LZ201121)

王国兴(1976－)，男，甘肃天水人，副教授，硕士，研究方向:图论及其应用.