一类具多偏差变元的p－Laplacian中立型Rayleigh方程的周期解

董冉冉，尹红云，张道祥

（安徽师范大学数学与计算机科学学院，安徽芜湖 241000）

一类具多偏差变元的p－Laplacian中立型Rayleigh方程的周期解

董冉冉，尹红云，张道祥

（安徽师范大学数学与计算机科学学院，安徽芜湖 241000）

利用广义的Mawhin重合度理论研究了一类具多偏差变元的p－Laplacian中立型Rayleigh方程的ω－周期解问题，并得到了周期解存在的充分条件.

周期解；中立型Rayleigh方程；偏差变元

0 引 言

中立型泛函微分方程吸引着众多学者的研究兴趣［1－4］，主要因为它能够为诸如生物、电子、机械和经济等众多领域提供良好的数学模型，以及对其研究具有重要的理论意义.特别地，人们近年来开始关注具偏差变元的p－Laplacian中立型Rayleigh方程［5－6］.文［5］利用拓扑度理论和一些分析技巧研究了具一个偏差变元的p－Laplacian中立型Rayleigh方程（φp（（x（t）－cx（t－σ））′））′＋f（x′（t））＋g（x（t－τ（t）））＝e（t）.而文［6］则将这种类型的方程（φp（（x（t）－cx（t－σ））′））′＋f（x′（t））＋α（t）g（x（t－τ（t）））＝e（t）转化为一个二维系统，进而利用Mawhin重合度理论讨论了其周期解.

本文在［5－6］的基础上进一步研究了一类具多偏差变元的p－Laplacian中立型Rayleigh方程：

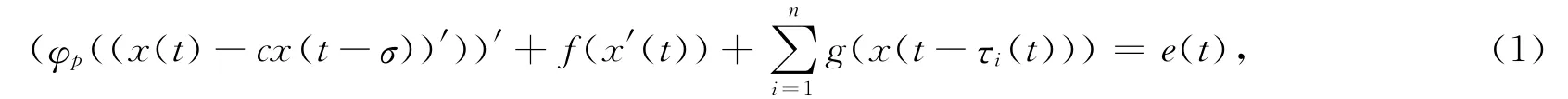
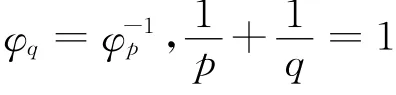
1 预备知识

为叙述方便，首先引入以下记号：

下面介绍广义的Mawhin重合度理论（Extension of Mawhin's continuation theorem）.

定义1［7］设X，Z是两个Banach空间，其模分别为‖·‖X，‖·‖Z.如果连续算子M：X∩domM→Z满足：（i）ImM：＝M（X∩domM）是Z的一个闭子集；（ii）KerM：＝｛x∈X∩domM：Mx＝0｝与Rn（n＜∞）是线性同构的.则称M是拟线性的.

定义2［4，7］设Ω⊂X是有界开集，其原点θ∈Ω.称Nλ→Z，λ∈［0，1］在上是M－紧的，如果存在Z的子集Z1满足dimZ1＝dimKerM，并且算子R：×［0，1］→X2是连续紧的使得对λ∈［0，1］有

（a）（I－Q）Nλ）⊂ImM⊂（I－Q）Z，

（b）QNλx＝θ，λ∈（0，1）⇔QNx＝θ，∀x∈Ω，

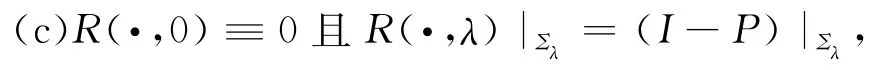
（d）M［P＋R（·，λ）］＝（I－Q）Nλ，λ∈［0，1］，

其中X2是KerM在X中的补空间，即X＝KerM⊕X2；投影算子P，Q满足ImP＝KerM，ImQ＝Z1，N＝N1，Σλ＝｛x∈：Mx＝Nλx｝.

引理1［4，7］设X，Z是两个Banach空间，其模分别为‖·‖X，‖·‖Z，且Ω⊂X是一个非空有界开集.若M：X∩domM→Z是拟线性的，Nλ→Z，λ∈［0，1］在上是紧的.并假设下列条件成立：

（H1）Mx≠Nλx，∀（x，λ）∈∂Ω×（0，1）；

（H2）QNλx≠0，∀x∈KerM∩∂Ω；

（H3）deg｛JQN，Ω∩KerM，0｝≠0，J：ImQ→KerM是同构映射.

则方程Mx＝Nx在domM∩中至少存在一个解.

引理2［8］设s，σ∈C（R，R）且s（t＋ω）＝s（t），σ（t＋ω）＝σ（t）.若函数t－σ（t）存在唯一的反函数μ（t），∀t∈R.则s（μ（t＋ω））＝s（μ（t））.

引理3［5］如果｜c｜≠1，p≥1，则A在Cω上存在连续有界的逆，且

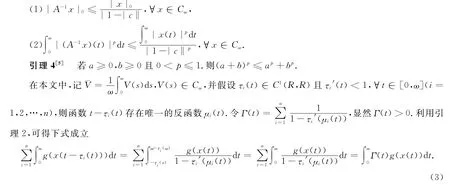
2 主要结果

设

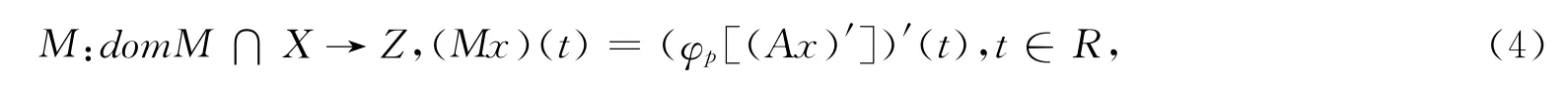
第二步.令Ω2＝｛x∈KerM：QNx＝0｝，下面证明Ω2也是一个有界集.对∀x∈Ω2，有

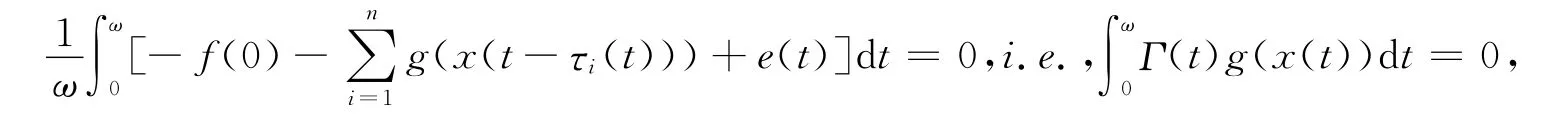
显然，存在一个常数t0∈［0，ω］使得Γ（t0）g（x（t0））＝0，即g（x（t0））＝0.根据［W2］，则有｜x｜＜d.故Ω2是一个有界集.

第三步.令Ω＝｛x∈X：‖x‖＜D｝，其中D＝max｛D0，D2，d｝＋1.不难看出对∀（x，λ）∈∂Ω×（0，1），有Ω1∪Ω2⊂Ω.由上述证明可知引理1中的条件（H1）和（H2）都是满足的.下证条件（H3）也是满足的.作同伦变换H（x，μ）＝μx－（1－μ）JQNx，x∈∩KerM，μ∈［0，1］.其中J：ImM→KerM是同构映射，且Jx＝x，x∈R.对∀x∈∂Ω∩KerM，有x＝m，且｜m｜＝M，故

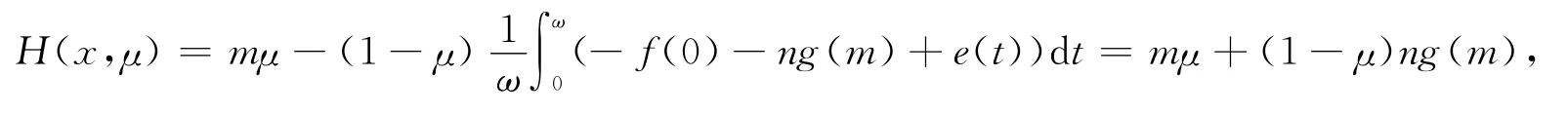
从而有mH（x，μ）＝m2μ＋（1－μ）nmg（m）.根据［W2］，则有mg（m）＞0，故H（x，μ）≠0.利用度理论得deg｛JQN，Ω∩KerM，0｝＝deg｛H（x，0），Ω∩KerM，0｝＝deg｛H（x，1），Ω∩KerM，0｝≠0.

故方程（1）至少存在一个ω－周期解.

［1］Zhu Yanling，Lu Shiping.Periodic solutions forp－Laplacian neutral functional differential equation with deviating arguments［J］.Math Anal Appl，2007，325（1）：377－385.

［2］Wang Kai，Zhu Yanling.Periodic solutions for a fourth－orderp－Laplacian neutral functional differential equation［J］.Journal of the Franklin Institute，2010，347（7）：1158－1170.

［3］Gao Fabao，Zhang Wei.Periodic solutions for ap－Laplacian－like NFDE system［J］.Journal of the Franklin Institute，2011，348（6）：1020－1034.

［4］Du Bo，Hu Xueping.Periodic solutions for a kind of Duffing typep－Laplacian neutral equation［J］.Acta Appl Math，2010，110（1）：167－179.

［5］Peng Shiguo.Periodic solutions forp－Laplacian neutral Rayleigh equation with a deviating argument［J］.Nonlinear Anal，2008，69（5－6）：1675－1685.

［6］Du Bo，Hu Xueping.Periodic solutions to ap－Laplacian neutral Rayleigh equation with deviating argument［J］.Applications of Mathematics，2011，56（3）：253－264.

［7］Ge Weigao，Ren Jingli.An extension of Mawhin's continuation theorem and its application to boundary value problems with ap－Laplacian［J］.Nonlinear Anal，2004，58（3－4）：477－488.

［8］Lu Shiping，Ge Weigao.Existence of positive periodic solutions for neutral population model with multiple delays［J］.Appl Math Comput，2004，153（3）：885－902.

Periodic Solutions for a Kind ofp－Laplacian Neutral Rayleigh Equation with Deviating Arguments

DONG Ran－ran，YIN Hong－yun，ZHANG Dao－xiang

（College of Mathematics and Computer Science，Anhui Normal University，Wuhu 241000，China）

By using the extension of Mawhin's continuation theorem，the paper obtained some new sufficient conditions for the existence forω－periodic solutions ofp－Laplacian neutral Rayleigh equation with deviating arguments.

periodic solution；neutral Rayleigh equation；deviating argument

O175.6 MSC2010：34C25；34B15

A

1674－232X（2012）02－0174－07

11.3969/j.issn.1674－232X.2012.02.016

2011－06－29

安徽高校省级科学研究项目（KJ2010B346）；安徽高校省级优秀青年人才基金项目（2010SQRL0256ZD，2011SQRL022ZD）.

张道祥（1979—），男，副教授，主要从事微分方程，流体力学研究.E－mail：zdxiang1012＠sina.com