基于Solidworks的阿基米德蜗轮蜗杆的建模与装配

马宝丽，朱志伟

（杭州师范大学钱江学院，浙江杭州 310012）

基于Solidworks的阿基米德蜗轮蜗杆的建模与装配

马宝丽，朱志伟

（杭州师范大学钱江学院，浙江杭州 310012）

通过对阿基米德蜗轮蜗杆的整体结构分析，首先建立了中间平面内蜗杆齿廓与蜗轮齿廓以及螺旋线方程；接着采用Solidworks2010软件，分别对阿基米德蜗轮蜗杆进行三维建模，并进行装配。参数化的三维设计与装配既缩短了设计周期，也为后续进行的有限元分析、机构仿真提供了必要前提条件.

阿基米德蜗轮蜗杆；Solidworks；三维建模；装配

在工程应用中，阿基米德圆柱蜗轮蜗杆的类型结构应用较为广泛，因此，本文以阿基米德蜗轮蜗杆为例，采用Solidworks2010为建模工具，实现了蜗杆、蜗轮零件的三维参数化造型与装配.其造型的精确性高，为后续进行的有限元分析、机构仿真和数控加工等提供了必要条件［1－2］.

1 阿基米德蜗杆的建模方法

对于蜗杆零件来说，蜗杆的结构相对简单，从切削原理分析，与螺纹基本相似［3］.蜗杆的整个螺旋齿是由一梯形轴剖面围绕蜗杆轴线作螺旋运动所形成的.各轴剖面内的齿廓相同，为等腰梯形，如图1所示.

1、3两点的坐标方程见式（1），2、4两点分别与1、3点关于y轴对称，因此，2、4两点坐标方程在此省略.

其中：齿距pa＝πm；压力角α＝20°；齿根高hf＝＋c＊）m；分度圆半径r1＝mq/2；齿顶高ha＝；齿顶高系数＝1；顶隙系数c＊＝0.2.其中m为模数，q为蜗杆直径系数.

2 阿基米德蜗轮轮齿的建模方法

2.1 渐开线齿廓曲线方程

在中间平面内，蜗轮蜗杆的啮合相当于齿轮和齿条的啮合传动［4］.蜗轮在中间平面内的齿廓形状是渐开线，如图2所示.

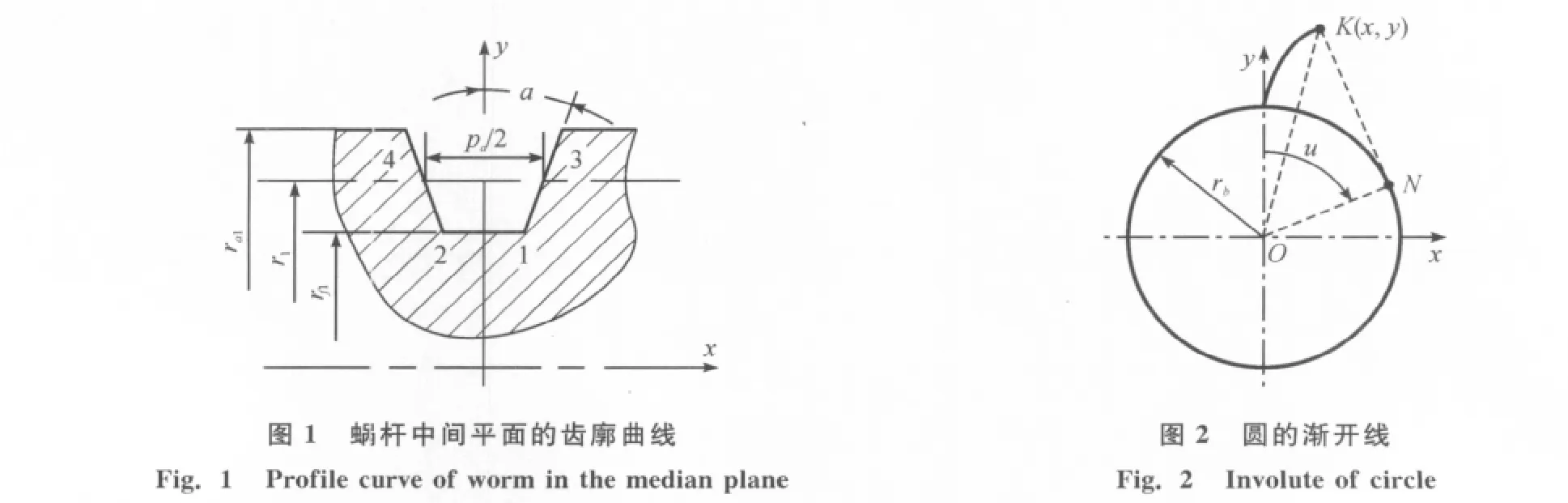
参照图2，结合渐开线的性质可以得出渐开线上任一点K的坐标：

式中：基圆半径rb＝r2cosα，r2＝mz2，滚角u的单位是弧度.

2.2 螺旋引导线方程

从图3可以看出，蜗轮的螺旋线是蜗杆螺旋线的一部分.

蜗轮分度圆的螺旋引导线上任意点的坐标：

图3 蜗轮蜗杆螺旋线Fig.3 The helix of worm wheel and worm

式中：中心距a＝r1＋r2；螺旋升角γ＝β2；θ的变化范围在－π/2～π/2，单位为弧度.

3 阿基米德蜗轮蜗杆建模与装配实例

取一对蜗轮蜗杆进行三维设计和装配，主要尺寸参数为：模数m＝4mm，蜗杆分度圆直径d1＝40mm，直径系数q＝10，螺旋升角γ＝21°48′05″，头数z1＝1，蜗轮齿数z2＝40，d2＝160mm，中心距a＝100mm，宽度B＝30mm.

3.1 阿基米德蜗杆建模

正如前面所述，蜗杆的建模比较简单.如图4所示，首先建立齿顶圆柱基体，此处根据需要可详细构建蜗杆的其它处细微结构；其次建立螺旋线，螺旋线的直径等于分度圆柱直径；再次是绘制齿槽截面，该截面所在平面一定在轴剖面上，因此此处参考面的建立尤为关键；最后通过扫掠切除命令生成完整的蜗杆，如果是多头的，还需圆周阵列z1个.

图4 蜗杆Fig.4 Worm

3.2 阿基米德蜗轮建模

阿基米德蜗轮的建模过程相比蜗杆要复杂的多，特别是齿槽齿廓的建立.蜗轮建模流程图如图5所示.

图5 流程图Fig.5 Chart

根据给定参数，计算蜗轮的各相关尺寸［5］.接下来，首先建立蜗轮的基体特征，特征的建立比较简单，如图6所示.其次是建立引导线，轮齿的引导线就是蜗杆分度圆上的螺旋线的一部分，在软件中实现也比较简单，在此需注意，在中间平面两侧的螺旋线需要分别生成.

如图7右侧的齿廓曲线旋转θ0角后，相对于y轴镜像生成左侧齿廓，然后再根据计算的数据生成齿顶圆和齿根圆，进行修剪后，它们所围成的一个封闭区域就是阿基米德蜗轮轮齿在中间剖面上的齿槽轮廓.但在实际加工中，滚刀刀尖存在一定的圆角，齿侧根部的曲线并非是完整的渐开线，而是一段过渡曲线.但过渡曲线参数十分复杂，这里就直接采用齿侧与齿底圆的倒圆来简化，倒圆半径取2mm，如图8所示.

通过扫描切除特征操作，生成一个齿槽.圆周阵列z个扫描切除特征，生成蜗轮的轮齿部分.最后是蜗轮的详细结构的设计，如钻孔、开槽等操作，蜗轮的整体结构如图9所示.

3.3 阿基米德蜗轮蜗杆装配

装配的时候，在蜗轮的定义中添加一条线，这条线的位置是蜗杆轴的位置；然后进行装配，先添加蜗轮，再添加蜗杆，显示所有线条，之后定义蜗杆的轴和蜗轮的线条重合，如图9所示.装配关系确定以后，可进行装配体干涉检查.

4 总 结

采用SolidWorks2010，可方便快捷地实现阿基米德蜗杆蜗轮三维建模与装配.在阿基米德蜗杆蜗轮设计中，三维CAD技术，使得结构设计直观，让人一目了然；三维CAD技术的参数化，可以有效地提高产品技术含量和质量，缩短机械设计周期，从而提高生产效率.阿基米德蜗杆蜗轮的设计与装配为后续的运动分析、力学分析、虚拟装配等奠定了良好的基础，具有较高的实用价值.

［1］郗向儒，韩锐，阮静.基于SolidWorks的运动仿真研究［J］.机械设计，2004，21（5）：50－52.

［2］李俊源.基于SolidWorks的蜗轮蜗杆三维参数化设计［J］.长春理工大学学报：自然科学版，2006，39（1）：98－100.

［3］江磊，王玉兰.基于SolidWorks的阿基米德蜗杆蜗轮经验交流建模方法探讨［J］.机械与电子，2007（3）：67－70.

［4］孙桓，陈作模.机械原理［M］.北京：高等教育出版社，2002：201－203.

［5］张黎骅，郑严.新编机械设计手册［M］.北京：人民邮电出版社，2008：468－476.

Modeling and Assembling of Archimedes Worm and Worm Wheel Based on Solidworks

MA Bao－li，ZHU Zhi－wei

（Qianjiang College，Hangzhou Normal University，Hangzhou 310012，China）

Through the structure analysis of Archimedes worm and worm wheel，the paper established the flank profile of worm and worm wheel as well as helix equations in the median plane，3Dmodeled Archimedes worm and worm wheel and assembled with Solidworks2010.The parameterized 3Ddesign and assembling shortened the design cycle，and provided the prerequisites for the finite analysis and mechanism simulation in subsequent works.

Archimedes worm and worm wheel；solidworks；3Dmodeling；assembling

TH132.4；TP391.9

A

1674－232X（2012）01－0077－04

11.3969/j.issn.1674－232X.2012.01.017

2011－08－30

杭州师范大学钱江学院科研基金项目（2011QJJL10）.

马宝丽（1977—），女，讲师，机械电子工程专业博士研究生，主要从事精密超精密加工、机械原理与设计、噪声与振动控制研究.E－mail：mabaoli＿77＠163.com