基于MATLAB 的一种高精度级联Sigma－Delta 调制器的结构设计

张 敏，林 伟

(福州大学福建省微电子集成电路重点实验室，福州35002)

现代数字集成电路的速度和集成度逐年提高，这要求系统中的信号处理能力不断增强。Sigma－Delta调制器由于其高精度的性能和低功耗被广泛用于系统的接收器中［1－3］。不仅如此，Sigma－Delta 调制器还具有将环路滤波器作为消除锯齿滤波器的优点［4］。可是，利用单环的Sigma－Delta 高阶调制器具有稳定性差，与理想调制器相比性能大大降低的缺点。而MASH(Multi－Stage－Noise－Shaping)级联多位量化器的拓扑框架结构可以克服单环高阶这一缺点。本文提出了一种时间上连续的2－2－2 级联Sigma－Delta 调制器拓扑结构，该结构是一种兼顾调制器稳定性的同时，能够获得高精度要求的良好选择。

1 级联Sigma－Delta 调制器结构

1.1 通用级联Sigma－Delta 调制器结构

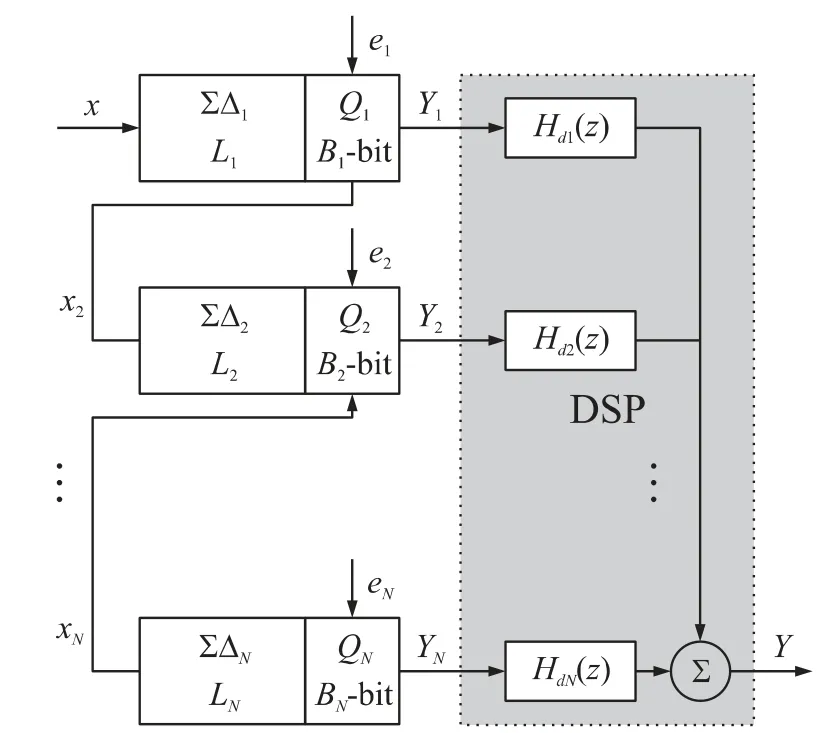
图1 N 级通用级联Sigma－Delta 调制器

一个通用的级联Sigma－Delta 调制器结构如图1和图2 所示。该结构由N 级Sigma－Delta 调制器组成，每一级调制器对带有由前级产生的量化误差的信号进行再调制，其对应的位于数字区域的输出Yi经过适当处理并加以合并，最终消除除了最后一级的所有N 级量化误差。这种误差产生于所有调制器的输出部分，该输出信号已通过级数等于所有级数总和的功能模块的整形操作。此外，由于各个反馈环路都位于本级内部，所以该通用级联Sigma－Delta 调制器结构不具有级间反馈，这推导出稳定的高阶整形只能通过一阶或者两阶Sigma－Delta 调制器的级联来获得。该多级Sigma－Delta 调制器的性能类似于一个理想高阶且不带有非稳定性问题的调制器性能。

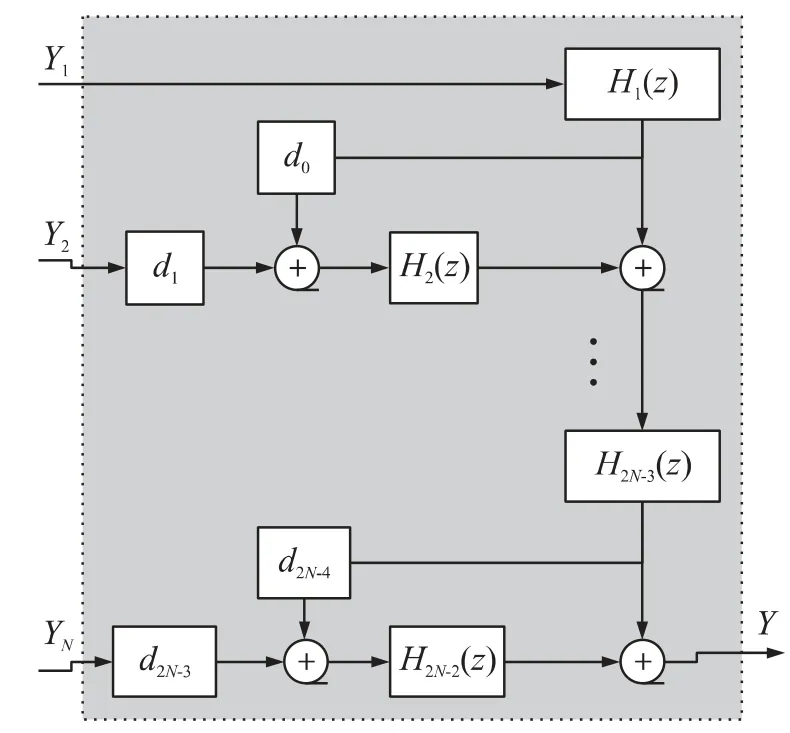
图2 数字信号处理区

1.2 经典的三阶2 级级联Sigma－Delta 调制器参数设定

三阶2 级级联Sigma－Delta 调制器是最基本的级联调制器，该调制器级数最少，但却包含了一阶和二阶完整的Sigma－Delta 调制器。下面给出具体的推导过程。

如图3 所示，该结构的调制器，其第1 级是一个二阶Sigma－Delta 调制器，其第2 级是一个一阶Sigma－Delta 调制器(两部分已分别用虚线方框围住)，现在我们分析其拓扑结构。

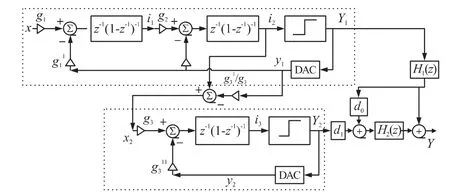
图3 三阶二级级联Sigma－Delta 调制器(2－1)

使用线性分析方法，第1 级在Z 域的输出为:

式中gq1是量化器增益，E1(z)是量化误差。接下来的关系式是在第1 级第二阶整形操作中导出:

另一边，下面第2 级的输出是:

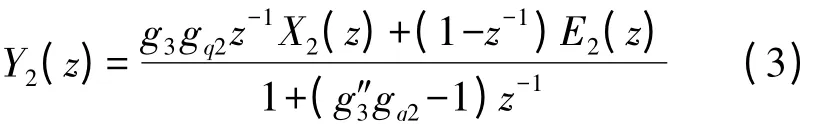
式中的X2(Z)代表该级的输入，gq2是其量化器的增益，E2(z)是相对应的量化误差。如图3 所示第2 级的输入是一个1 级输入和输出信号的组合，具体如下:

为了从式(3)中得到对第2 级量化误差的一阶整形，一下条件必须满足:

利用以上公式最终得到X2(z)、Y2(z):

以上两个结果包括了输入信号，来自第2 级的一阶整形量化误差和来自第1 级的整形与非整形量化误差。

该结构的输出可以在数字区域处理，处理后得到一个没有E1(z)的输出。为了达到这一目的，调制器的输出不妨写成:

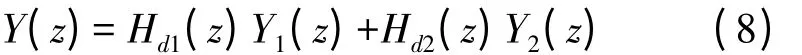
其中Hd1(z)、Hd2(z)分别是:

其中各个部分是:

综合以上公式可得:

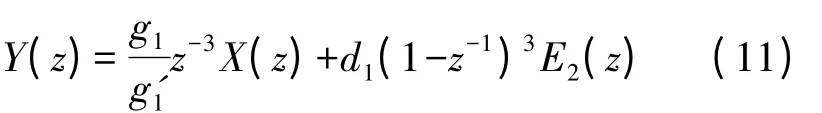
公式(11)，根据其物理含义可改写为:

从式(11)可以看出其性能相当于一个理想三阶调制器，但因为其应用级联方式，所以性能更稳定。该调制器的带内量化误差功率为:

式中Δ2是第2 级量化器的量化步阶。到此直接给出N 级级联Sigma－Delta 调制器的输出和量化误差功率:

其中L=L1+L2+…+LN，d2N－3是比例因子，它与放大最后一级量化误差的积分器有关。

2 2－2－2 级联Sigma－Delta 调制器结构

如图4 所示，给出的是一个六阶3 级级联Sigma－Delta 调制器结构，该结构是建立在N 级通用级联调制器框架的基础之上，其他形式的的结构，其表达方式也许有不同。对于确定这个六阶3 级级联调制器，以下各点是考虑因素:(1)降低决定精度损失的比例因子，(2)提高过载级数，以获得一个较高的SNR，(3)降低积分器的输出浮动。由于推导过程如上面经典的三阶2 级级联Sigma－Delta 调制器所示，下面省略过程，直接给出图4 结构所需的参数条件:

图4 六阶三级级联Sigma－Delta 调制器

根据参数条件，给出该2－2－2 级联Sigma－Delta调制器结构各个参数:g1=0. 5、g'1=0. 5，g2=0.5、g'2=0.5，g3=1、g'3=0.5、g″3=0.5，g4=0.5、g'4=0.5，g5=1、g'5=0. 5、g″5=0. 5，g6=0. 5、g'6=0. 5;d0=1、d1=2、d2=0、d3=0.25。

图5 显示出，2－2－2 级联Sigma－Delta 的SQNR曲线在过采样率为32，SQNR 的峰值为89.0 dB。而在图6 中也显示，在输入等级为－3.0dB，采样率为32 不变情况下，SQNR 的峰值为87.9 dB。其精度与传统非级联结构相比是有显著提高的［5］。

图5 SQNR 的输出点图

图6 2－2－2 级联结构的SQNR 输出曲线图

3 结束语

本文给出了通用级联Sigma－Delta 结构，从经典的2－1 级联结构进行推导提出了整个给出参数步骤，并确定了2－2－2 级联结构的参数。通过在Simulink 环境下的仿真，得出其SQNR 性能参数。该级联调制器结构，具有内在的反锯齿滤波器，能够使通信系统中的低功率集成接收器性能明显提高。

［1］ Veldhoven R.A Tri－Mode Continuous Time Modulator with Switched Capacitor Feedback DAC for a GSM－EDGE/CDMA2000/UMTS Receiver［J］.IEEE ISSCC Dig.Tech，2003，4(2):60－61.

［2］ Philips S.A 4.4 mW 76 dB Complex ADC for Bluetooth Receivers［J］.IEEE ISSCC Dig.Tech.，2003，6(2):64－65.

［3］ Zwan E.A 0.2 m WCMOS Modulator for Speech Codingwith 80 dB Dynamic Range［J］.IEEE J.Solid－State Circuits，1996，31(2):73－80.

［4］ Longo L，Hairapetian A，Seiyama K.A 90 dB SNR，2.5 MHz Output Rate ADC Using Cascaded Multibit Modulation at 8 Oversampling Ratio［J］.IEEE ISSCCDig.Tech.Papers.2000，5(1):38－39.

［5］ Hoseini H，Kale I.On the Effects of Finite and Nonlinear DC Gain on the Switched－Capacitor Delta－Sigma Modulators［J］.IEEE Int.Symp.Circuits Systems，2005，11(3):47－50.

［6］ Tille T，Sauerbrey J，Schmitt D. A Low Voltage MOSFET Only Modulator for Speech Band Applications Using Depletion Mode MOS Capacitors in Combined Series and Parallel Compensation［J］.IEEE ISCAS，2001，1(3):76－79.

［7］ Sauerbrey J，Tille T，Schmitt D.A 0.7 V MOSFET Only Switched Opamp Modulator in Standard Digital CMOS Technology［J］.IEEE J.Solid－State Circuits，2002，37(12):62－69.

［8］ Keskin M，Moon U K，Gabor C.A 1 V 10 MHz Clock－Rate 13－Bit CMOS Modulator Using Unity－Gain－Reset Opamps［J］. IEEE J.Solid－State Circuits，2002，37(7):17－24.

［9］ Li Qunying，Laker K R. A 1.2 V，38 W Second－Order Modulator with Signal Adaptive Control Architecture［J］. IEEE 2nd Dallas CAS Workshop on Low Power/Low Voltage Mixed－Signal Circuits and Systems，2001，27(1):23－26.

［10］ 刘顺兰，吴杰.数字信号处理［M］.西安:西安电子科技大学出版社，2003:12－17.

［11］ 易亭.高性能sigma－delta 模数转化器设计［D］:［博士学位论文］.上海:复旦大学，2002.