多相抽取滤波器的FPGA实现*

谢海霞，孙志雄

(琼州学院电子信息工程学院，海南三亚572022)

多速率指的是一个系统中存在着两种或者两种以上的信号采样率，多速率信号处理最早于20世纪70年代提出，具有重要的理论和工程价值。近10年来，随着大规模集成电路的发展和A/D、D/A采样率的不断提高，多速率数字滤波器和滤波器组在很多领域有着广泛的应用，如数字音频处理、语音处理及数字通信等。多速率信号处理是软件无线电系统中的基础理论，它通过内插和抽取改变数字信号的速率，以适应软件无线电系统中不同模块对信号速率的不同要求，使采样率降低的转换，称为抽取;使信号采样率升高的转换，称为内插。单独的抽取和内插实现抽样率转换计算量很大，为适用于实时系统，采取优化实现结构，使用多相分解，提高计算效率。在此讨论了滤波器的多相分解，及其FPGA实现的过程［1-5］。

1 多相分解的基本理论

当在IIR或者FIR滤波器和滤波器组中实现抽取或插值时，多相分解是非常有用的。下面以多速率抽取滤波器为例来说明多相分解的好处［6-7］。

对于图1中的抽取滤波器，如果H(z)是一个用直接型实现的长度为N的FIR滤波器，那么

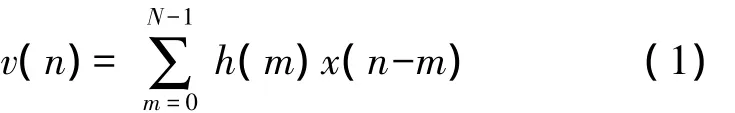
图1 M-抽取器的示意图

现在，对v(n)每M个点进行抽样一次作为下抽样器的输出。因此，在上式中只需在n=kM(k=1，2，)时计算v(n)的值即可，可以跳过其他中间的样值。这使得计算复杂度节省为原来的1/M。而利用多相分解可以达到相同的效果，下面进行具体的分析。

假设系统下抽样率为M，对于序列h(n)，其Z变换为:

由式(2)可得:

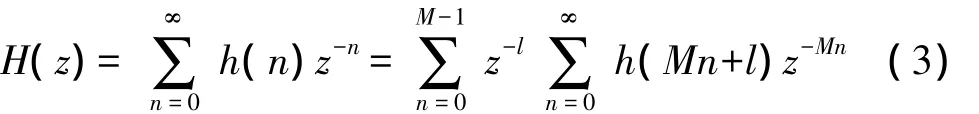
如果令

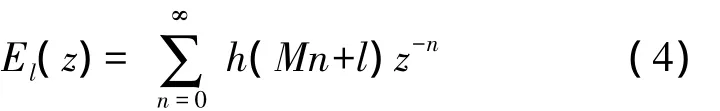
式(4)可以改写为:

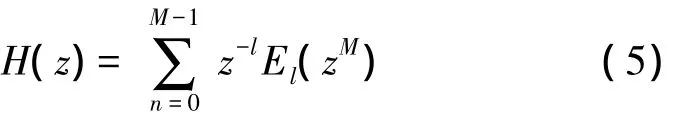
其中，h(Mn+1)被称为多相分量。考虑到h(n)为因果序列，以上各式求和都是从［0，∞］。对于任一序列，可以将求和扩展至［-∞，∞］。

多相分解对于FIR、IIR系统都适用。图2给出了基于多相分解的FIR系统的抽取器结构，其中抽取器的速率比后面的FIR滤波器El(zM)快M倍。滤波器El(zM)被称为多相滤波器。［8-10］

图2 FIR滤波器的多相分解图

对于低通滤波器的传输函数进行多相分解，得到图2中的高效抽取器结构，下面对图1中的抽取滤波器和多相分解的结构进行对比分析。对于前者，假设FIR滤波器长度为N，输入信号抽样周期为T=1。由于抽取器的输出y(n)可以从M倍下抽样滤波器的输出v(n)得到，故仅仅需要计算当n=…，-2M，-M，0，M，2M，…时的v(n)。因此，输出每个样本需要的计算量为N次乘法和(N-1)次加法。然而，随着n的增加，延时寄存器中存储的信号会不断地变化。因此全部的计算必须在一个抽样周期T中完成，而接下来的(M-1)个抽样周期中，运算单元就保持空闲。但是对于图2中的多相结构，假设子滤波器El(zM)的长度是Nl，则。第l个子滤波器输出每个样本需要计算N1次乘法和(N1-1)次加法，因此对于整个结构，抽取器输出每个样本仍需要计算N次乘法和(N-1)次加法。然而，运算单元在输出抽样周期MT的所有时刻都在工作，这使得计算更加有效。

2 多相抽取滤波器的实现

设实现一个长度为4的FIR多相抽取滤波器，实现M=2倍下采样。其传递函数为:

2.1 设计实例的Verilog HDL实现

首先将滤波器进行量化，字长为8 bit，则:

将式(6)化在M=2时的多相表示，得:

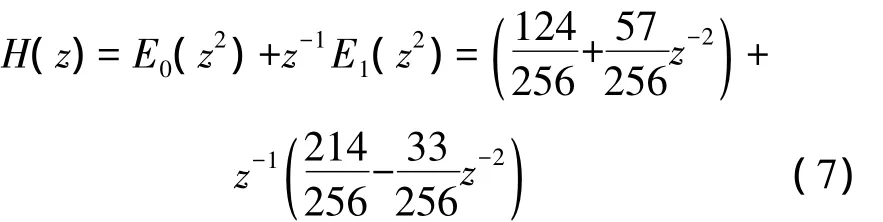
由(7)可知:

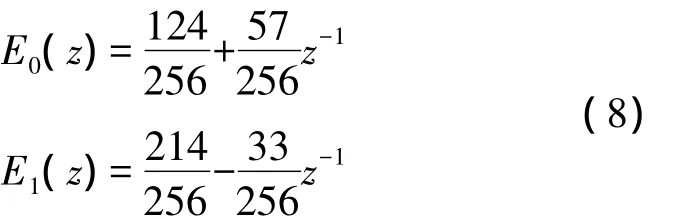
E0(z)和E1(z)分别是第0个多相分量和第1个多相分量。

用Verilog HDL语言实现该2相抽取滤波器。

系数运算的部分程序:

程序在QuartusⅡ中编写完毕后，进行波形仿真，仿真结果如图3所示。clk是输入信号的速率，clk2是输入信号速率的一半，为2相分量的信号传输速率，x_in 是输入信号，序列为{0，1，2，3，4，5，6，7，8}，y_out是输出信号，序列为{0，1，4，7，10}。

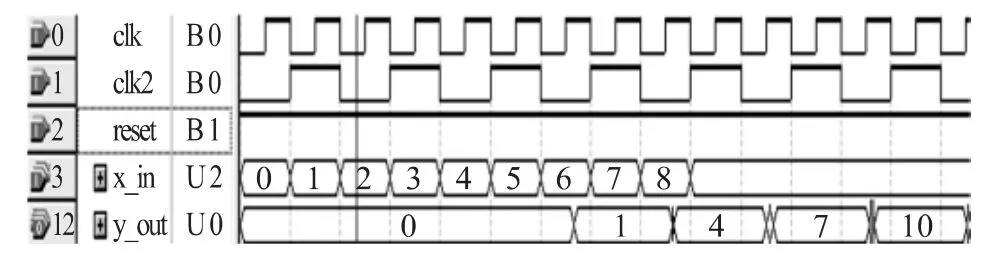
图3 多相滤波器的波形仿真图

2.2MATLAB仿真验证

可以用MATLAB来验证该设计的正确性。

MATLAB仿真波形图(图4)和图3的仿真结果一致［11-12］，因此该设计是正确的，最后把生成的编程数据文件下载到FPGA芯片中即可。

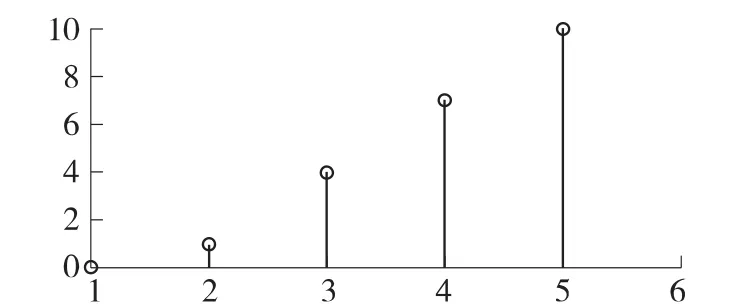
图4 MATLAB验证仿真结果图

3 结束语

对于多相抽取滤波器，各个多相分量的工作速率是输入信号速率的1/M，速率下降，运算单元在M个单位时刻都在工作，使用多相分解不但可以在抽样率转换的过程中去掉许多不必要的计算，从而大大提高运算的速度。本文介绍的多相滤波器的FPGA实现的设计、验证方法都是可行的，而且在实际使用的时候，人们可以根据应用不同的场所在程序里可以很方便地改变滤波器的参数，以简便的操作来达到降低系统的计算复杂性的功能。设计不仅对抽取滤波系统的多相结构适用，而且对内插系统的多相分解的实现也有一定的参考作用。

［1］陶然，张惠云，王越.多抽样率数字信号处理理论及其应用［M］.北京:清华大学出版社，2007:4.

［2］高媛菲.数字下变频中抽取滤波器的设计［J］.桂林电子科技大学学报，2009，29(6):467-471.

［3］雷能芳.基于FPGA的CIC抽取滤波器设计与实现［J］.计算机与数字工程，2012(1):137-139.

［4］刘彬彬，林伟.基于Matlab和FPGA的CIC滤波器的设计［J］.电子器件，2010，33(2):231-234.

［5］潘桃莉，谢光忠，周云，等.改进的抽取滤波器设计［J］.微处理机，2011(1):7-10.

［6］王福维，程乃平，倪淑艳.基于FPGA的CIC抽取滤波器的设计与实现［J］.计算机工程与应用，2011，47(8S):415-418.

［7］Meyer-Baese，著.刘凌，胡永生，译.数字信号处理的 FPGA实现［M］.北京:清华大学出版社，2003.

［8］田耘，徐文波，张延伟.无线通信FPGA设计［M］.北京:电子工业出版社，2007.

［9］Vaidyanathan P P.Filter Banks in Digital Communications［J］.IEEE Circuits and Systems Magazine，2001，1(2):4-25.

［10］陈后金，薛健，胡健.数字信号处理［M］.北京:高等教育出版社，2008.

［11］王旭东，潘广祯.MATLAB及其在FPGA中的应用［M］.北京:国防工业出版社，2005.

［12］陈怀琛.数字信号处理教程-MATLAB释义与实现［M］.北京:电子工业出版社，2004.