基于Fourier－Mellin的图像配准算法研究

郭清宇，崔伟民

（中原工学院，郑州450007）

1975年，Kuglin C D等提出了相位相关算法，用来处理平移图像的对齐（alignment）［1］，该算法具有良好的信噪比、尖锐的相关峰（correlation peak）、易于实现且复杂度低等优势，能以较高的精度求出图像的平移量（displacement）；1994年，Chen Q等提出了基于Fourier－Mellin变换的算法，该算法拓展了相位相关算法，通过对图像的幅度频谱（magnitude spectra）进行对数－极（Log－Polar）坐标变换［2－4］，将时域内的旋转和缩放问题转化为频域内的平移问题，实现了存在旋转、缩放 平移变换的两幅图像之间的配准；Chen Q等和Reddy B S等通过大量实验，发现基于Fourier－Mellin变换的算法除具有较高的精度外，对诸如一致性的照明变化、图像内容部分失真或遮挡、加性噪声等具有很强的鲁棒性，并且相对于其他配准方法运算量较少［2－3，5］.但是基于 Fourier－Mellin变换的算法在实现过程中会遇到一些问题，导致配准算法精度不高或失效.例如，由于图像的截断和离散化［6］，产生了不连续和边界效应；离散傅里叶变换与有限采样图像旋转的不可交换性，产生了与旋转相关的混叠（aliasing）现象［7］；对图像幅度频谱在径向方向（radial direction）重采样，产生了不均匀采样和插值错误［2，4］.本文分析了降低算法配准精度的主要原因，利用加窗、滤波等方法改进了图像配准算法，并通过实验表明了新算法能取得较好的配准效果.

1 理 论

1.1 相位相关算法

若图像f2（x，y）是由图像f1（x，y）平移（x0，y0）得到，即

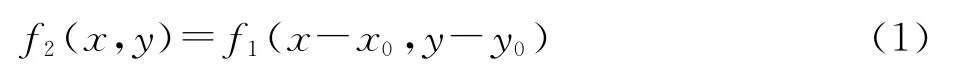
相应的傅里叶变换［6，8－9］为：

F1（ξ，η）＝F（f1（x，y）），F2（ξ，η）＝F（f2（x，y））

其中，F（·）为傅里叶变换.则

不妨定义图像相位相关函数PC（u，v）为：

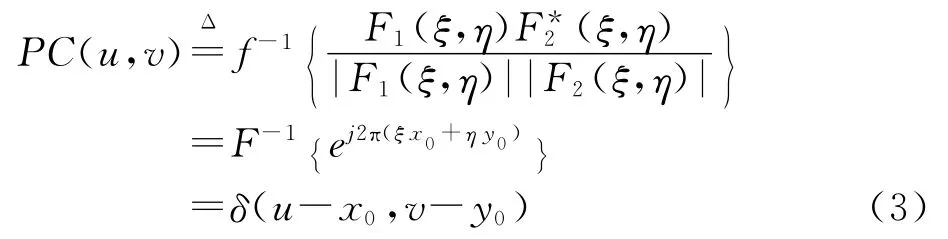
其中，F－1｛·｝为傅里叶反变换［6，8－9］；F＊2（ξ，η）为F2（ξ，η）的共轭.

由式（3）对互功率谱做傅里叶反变换，可得到一个二维冲激（Dirac）函数PC（u，v）.在理想情况下，此函数在（x0，y0）处产生函数值为1的相关峰，在其他点的函数值接近0，其峰值所在点即为配准图像的平移量（x0，y0）.这就是用相位相关算法求解配准图像的平移量的主要过程.

1.2 存在旋转、缩放 平移的图像变换

若图像f2（x，y）是由图像f1（x，y）旋转θ0角、缩放σ倍、平移（x0，y0）得到，则

对式（4）做傅里叶变换并取频谱幅度：

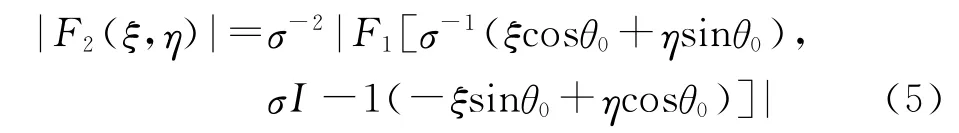
其中，｜·｜表示频谱幅度.

引入对数－极坐标系，不妨定义：

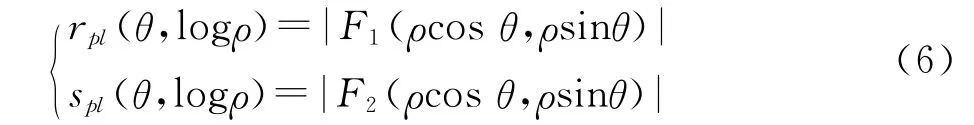
由式（5）和式（6）得出：

spl（θ，logρ）＝σ－2rpl（θ－θ0，logρ－logρ）

令λ＝logρ，k＝logσ，则：

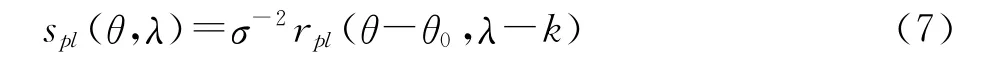
从式（1）和式（7）的比较可以看出，它们具有相同的形式.因此在对数—极坐标系下，对傅里叶频谱图应用相位相关算法，即可求得θ0、k，这样就得到了旋转角θ0、缩放因子σ.对图像f1（x，y）缩放σ倍、旋转θ0角，得到一个新图像f3（x，y），然后对图像f2（x，y）和图像f3（x，y）应用相位相关算法即可求得平移量（x0，y0）.

2 降低配准精度的原因和改善方法

2.1 图像的有限采样和截断误差

由于图像的有限采样和截断误差，对图像进行傅里叶变换将在频域内产生假象（artifact）.图像的边界效应产生的失真高频部分导致在频域内产生频谱泄露现象.这些集中在高频部分的伪能量，随着图像的旋转产生强烈的混叠现象.Harris F J于1978年提出，加窗可以消除图像的边界效应产生的频谱泄露现象［10］.本文利用blackman窗［8］来平滑边界，除去图像的边界效应产生的失真高频部分，减少了混叠现象，提高了相位相关算法的精度.

2.2 旋转引起的混叠现象

对于仅存在平移变换的待配准图像，相位相关算法的有效性和精确性已经被证明.但当存在旋转变换时，由于有限采样图像的旋转和离散傅里叶变换的不可交换性，在频域内产生了强烈的混叠现象.这种混叠现象随旋转角度的变化而变化.它对相位相关算法的影响表现在：在二维相位函数PC的函数图上产生了伪相关峰（false correlation peak）.从式（3）可知，相关峰高度之和为1，伪相关峰的出现必然减小真相关峰的高度值，使相位相关算法的精度降低；甚至伪相关峰可能比真相关峰还要高［7］，从而使相位相关算法失效［11］.这些混叠现象主要集中于低频部分，滤去这些低频部分，将大大提高相位相关算法的精度.Stone H S等人提出，去掉距频域原点N／4的圆周部分低频区域，可大大提高信噪比和相关峰值，从而提高求得的旋转角的精度［7］.Reddy B S等人提出，用高通滤波器来滤出傅里叶原点附近的低频部分，能较好地抑制混叠现象［5］.

2.3 由笛卡尔坐标系向对数－极坐标系转化的误差以及插值错误

从式（7）可知，采用对数－极坐标系表示法可将笛卡尔坐标系下的旋转和缩放变换转化为对数－极坐标系下的平移变换，如图1所示.假设图像的幅度频谱为R（u，v），R（u，v）可用原点在（N／2，N／2）处的 N×N的网格表示，其中u，v分别为笛卡尔坐标下的频率坐标.利用下列重采样函数将R（u，v）直接转化为对数－极坐标系下的M×K网格.其中，m代表离散的极坐标，m＝0，…，M－1；k代表离散的角坐标，k＝0，…，K－1.

图1 笛卡尔坐标系和对数－极坐标系下的图像

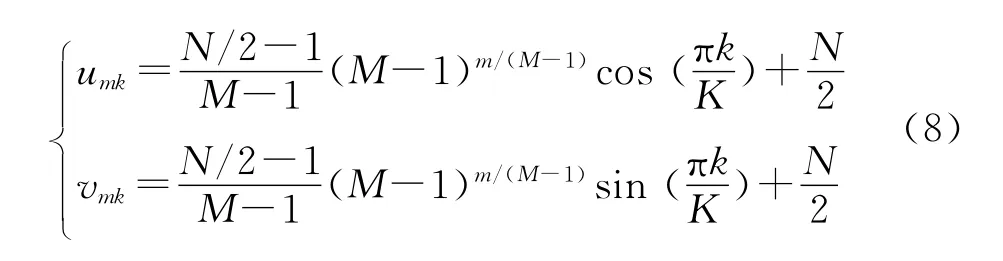
由式（8）可以看出，从笛卡尔坐标系向对数－极坐标系的转换是非线性的重采样过程.为了保证重采样的质量，采用二维线性插值.由于幅度频谱变化范围较大且不连续，可能导致假象出现.为了抑制这种假象，在重采样前对幅度频谱在径向方向（radial direction）利用hanning窗进行处理［8］.幅度频谱的径向坐标由于其对数变换而失真，产生了不均匀采样，导致了求得的缩放因子的精度下降.如果缩放因子太大或太小，本算法可能失效.Chen Q等对式（8）进行了误差分析，并经实验验证，缩放因子在［0.5，2］内可获得较高的精度［2］.

3 实 验

由以上分析可以看出，图像变换参数求解的顺序为：首先在频域内求出缩放因子及旋转角，然后在时域内求出平移量.如将原始图像称为参考图像，目标图像为参考图像仅经旋转、缩放、平移变换所得，则图像配准参数求解的具体步骤如下：

（1）对参考图像和目标图像加窗和填充，并进行傅里叶变换；

（2）对各自的傅里叶幅度频谱分别进行高通滤波；

（3）对各自的傅里叶幅度频谱的径向加窗后进行对数－极坐标变换；

（4）对得到的2幅傅里叶幅度频谱图像应用相位相关算法求出缩放因子和旋转角；

（5）按步骤（4）得出的图像变换参数对参考图像进行相应的缩放和旋转变换，得到一个新的图像，将其和目标图像应用相位相关算法求出平移量.

为了验证本文提出的算法的通用性及精度，用Matlab语言进行编程以实现本算法.

在实验中，用本算法估测出的变换参数和使用的实际变换参数如表1所示.

以表1中的第1组数据为例进行分析，如图2所示.图2中的目标图像（图2（b））由原始图像（图2（a））变换得到，实际所用旋转角、缩放因子、平移量分别为（25，1.6，（13，20））.对原始图像和目标图像进行配准，估测出变换参数为（25.3，1.593，（14，21））；利用估测出的数据进行配准，效果如图2（c）所示.

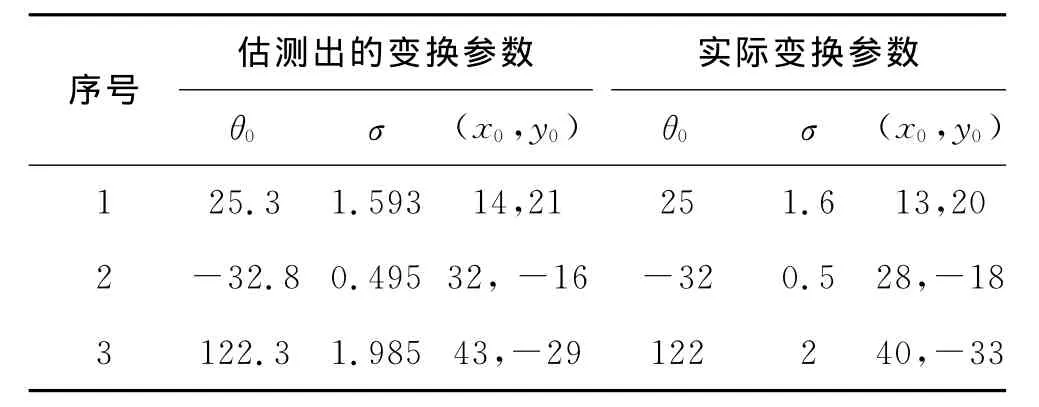
表1 估测出的变换参数与实际变换参数

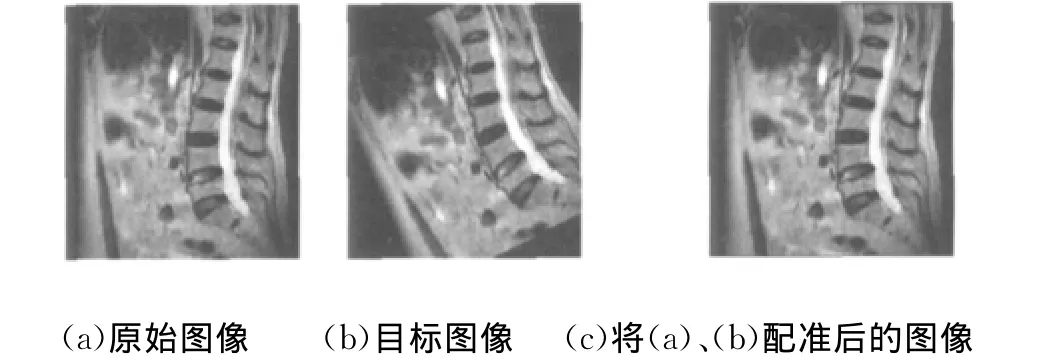
图2 表1中第1组数据的相关图像

为测试缩放因子的边界值，对图2中的原始图像，按表1中第2组与第3组数据进行分析（这里从略），也得到了较好的配准效果.

4 结 语

本文对基于Fourier－Mellin的图像配准算法进行了研究，分析了降低旋转和缩放的参数求解有效性和精度的主要原因，利用加窗、滤波等方法，增大了图像的信噪比，从而提高了配准算法的有效性和精度.实验结果表明，本算法的配准效果较好.虽然本算法可以较好地处理存在旋转、较小缩放和平移差异的图像配准问题，但对于更大的缩放变换，存在算法失效问题，需进一步研究.

［1］Kuglin C D，Hines D C.The Phase Correlation Image Alignment Method［C］／／Proceedings of the International Conference on Cybernetics and Society.New York：International Conference on Cybernetics and Society，1975：163－165.

［2］Chen Q，Defrise M，Deconinck F.Symmetric Phase－Only Matched Filtering of Fourier－Mellin Transforms for Image Registration and Recognition［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1994，16（12）：1156－1168.

［3］Zitova B，Flusser J.Image Registration Methods：A Survey［J］.Image and Vision Computing，2003，21（10）：977－1000.

［4］Wolberg G，Zokai S Robust.Image Registration Using Log－Polar Transform［C］／／Proceedings of the International Conference on Image Processing.Vancouver：International Conference on Image Processing，2000：493－496.

［5］Reddy B S，Chatterji B N.An FFT－Based Technique for Translation，Rotation and Scale－Invariant Image Registration［J］.IEEE Trans.Image Processing，1996，5（8）：1266－1271.

［6］Bracewell R N.The Fourier Transform and Its Applications［M］.3rd Edition.New York：McGraw－Hill，1999：150－290.

［7］Stone H S，Tao B，McGuire M.Analysis of Image Registration Noise due to Rotationally Dependent Aliasing［J］.Journal of Visual Communication and Image Representation，2003，14（2）：114－135.

［8］Smith S W.The Scientist and Engineer’s Guide to Digital Signal Processing［M］.California：California Technical Publishing，1997：141－296.

［9］Gonzalez R C，Woods R E.Digital Image Processing［M］.3rd Edition.Beijing：Publishing House of Electronics Industry，2010：221－325.

［10］Harris F J.On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform ［J］.Proceedings of the IEEE，1978，66（1）：51－83.

［11］Lucchese L，Cortelazzo G M，Monti C.High Resolution Estimation of Planar Rotations Based on Fourier Transform and Radial Projects［EB／OU］.［2012－08－26］.http：／／www.lw20.com／2011012960307296.html.