供应链模式下企业间利益分配演化博弈模型的建立

郭微微，陈凯怡

（1.中原工学院，郑州450007；2.河南工业大学，郑州450001）

供应链管理通过各个节点企业间的相互合作、协调一致的行动，降低供应链的运营成本，从而实现供应链利益的最大化.对于供应链中的节点企业，自身利益的最大化是吸引其加入供应链的最大诱因.作为独立实体，如果节点企业在供应链中的投入没有得到相应的回报，那么必将影响整个供应链的稳定性，对供应链的正常运作产生不利的影响.因此，公平合理的利益分配机制是保证供应链稳定运行和持续发展的关键因素，影响整个供应链的成败.本文将运用演化博弈理论对供应链企业间的利益分配问题进行研究，并建立其复制动态模型.

1 演化博弈模型的建立

一条完整的供应链包括供应商（原材料供应商或零配件供应商）、制造商（加工厂或装配厂）、分销商（代理商或批发商）、零售商（大卖场，百货商店，超市，专卖店，便利店和杂货店）以及消费者.本文研究的是整条供应链企业间的利益分配问题，考虑到各个节点企业间的供应关系比较相似，所以在建立模型时，以供应商与制造商之间的利益分配问题作为研究的对象，其他节点企业间的利益分配问题可以用类似的方法解决.

在供应链中，供应商与制造商是具有有限理性的，他们的决策过程由于受各种因素的影响，是一个复杂的调整过程，通过不断地模仿、学习、突变等，最终达到均衡的博弈结果.在模型中，我们假设供应商与制造商面临着2种策略选择：合作与不合作.合作主要是指供应商和制造商之间建立紧密的联系，除了简单的商品交易外，双方从各个环节都相互合作，提高整体的竞争优势.不合作主要是指供应商与制造商之间各自独立经营，双方只是存在单纯的交易关系.双方在考虑自身群体的因素和其他成员的策略选择情况的基础上，对其策略进行选择和调整［1］.所以，供应商与制造商之间的博弈属于两种群的演化博弈.

各假设信息如下：

f1（k）、f2（k）分别为供应商和制造商不合作时所获得的利润；

C1、C2分别为供应商和制造商选择合作时所投入的初始成本；

ΔS为供应商和制造商选择合作时所创造的超额收益；

β为供应商获得的合作产生的超额收益的分配系数，0＜β＜1.

博弈方：供应商和制造商，且双方具有有限理性；

策略：供应商和制造商的策略集均为（合作，不合作）；

策略的采用比例：供应商群体中采取合作的概率为x（0≤x≤1），不合作的概率为1－x；制造商采取合作的概率为y（0≤y≤1），不合作的概率为1－y. 因此，供应商和制造商之间的博弈矩阵如表1.

江苏省泰州引江河管理处高港枢纽位于长江下游北岸泰州市高港区口岸镇西北约3km处，枢纽节制闸和泵站采用闸站结合布置形式。高港枢纽节制闸共5孔，每孔净宽10 m，设计流量为440 m3/s，采用弧形钢闸门；泵站采用堤身式双向箱形流道结构,立轴双层进出水流道，配开敞式轴流泵9台，每台机组设置4扇平面钢闸门，可通过下层流道实现160 m3/s的自流引江。高港枢纽1999年建成时，节制闸和泵站的监控系统采用SUPCON JX-300型DCS集散控制系统，如图1监控系统部分所示，在中央控制室可实现对闸门的操作控制，并可采集闸门开高及上下游水位，实时显示。

表1 供应商和制造商博弈的支付矩阵

综上所述可得，供应商选择合作策略的期望支付为：

供应商选择不合作策略的期望支付为：

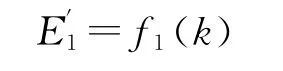
因此，供应商的平均期望支付为：

同理，制造商选择合作策略的期望支付为：

制造商选择不合作策略的期望支付为：

制造商的平均期望支付为：

由以上各式可得，供应商和制造商对x、y的复制动态方程为：

2 模型分析

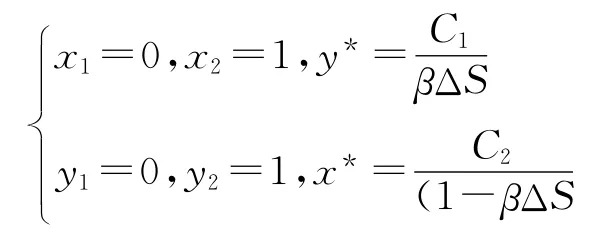
供应商与制造商间博弈的动态演化过程可以用图1进行描述［3］.其中，由2个不稳定的均衡点A和B以及鞍点D连成的折线ADB是系统收敛于不同状态的临界线.在折线ADB上方（ADBC部分），系统向（合作，合作）方向进行演化，收敛于演化稳定策略点C（1，1），此时供应商与制造商都会选择完全合作策略，两者之间形成了完全合作的关系；在折线ADB下方（ADBO部分），系统向（不合作，不合作）方向进行演化，收敛于点O（0，0），此时供应商与制造商都会选择不合作策略，双方各自完全独立经营.

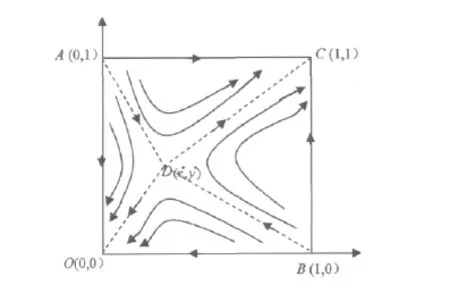
图1 供应商与制造商竞合关系演化相位图

3 分配系数β取值分析

根据以上分析，供应商与制造商演化博弈的长期均衡结果是完全合作还是完全不合作，取决于区域AOBD和区域ADBC的面积.当SADBC＞SADBO时，供应商与制造商合作的概率大于不合作的概率，系统将沿着路径DC向完全合作的方向演化；当SADBC＜SADBO时，供应商与制造商合作的概率小于不合作的概率，系统将沿着路径DO向完全不合作的方向演化；当SADBC＝SADBO时，供应商与制造商合作与不合作的概率是相等的，系统的演化方向不明确［1］.

供应商与制造商进入供应链的最终目的就是获得超额利益，在这里我们用β表示供应商获得的超额利益的分配系数，β的取值可以直接反映利益分配的合理性问题.下面讨论分析β的取值.

根据图1，得出区域AOBD的面积为

SAOBD对β求导有：

可见，利益分配系数β的取值与供应商与制造商合作时投入的初始成本有关，具体是取β1还是β2，视具体情况而定，β的取值范围为：0＜β＜1.

4 结 语

利益分配问题是实现供应链稳定发展的关键问题之一，因此，如何公平合理地对供应链的利益进行分配，已成为学者们的研究重点.本文运用演化博弈理论对供应链中供应商与制造商之间的博弈进行了演化分析，建立了供应商与制造商的复制动态模型，并在此基础上确定了分配系数的取值，实现了供应链利益的均衡分配.

［1］李惠杰，郭微微.农产品加工业供应链利益均衡分配博弈分析［J］.价值工程，2011（8）：34－35.

［2］Friedman D.Evolutionary games in Economics［J］.Econometrics，1991（5）：637－666.

［3］孙世民，陈会英.优质猪肉供应链合作伙伴有效竞合机制的进化博弈分析［C］／／第六届中国管理科学与工程论坛论文集.上海：上海财经大学出版社，2008.