2010年数学建模竞赛A题的计算方法研究

吴小庆,张 合

(西南石油大学理学院,四川成都610500)

问题描述:2010年数学建模竞赛A题问题2[1],对于实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。请利用罐体变位后在进出油过程中的实际检测数据,根据所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。

储油罐在此两种变位情况下,储油罐的形状不会发生改变,仅考虑小的变位,不会出现油的溢出,从而罐内油的体积就不会发生改变,即变位前后的油量总体积是不变量,与变位参数无关。所以由体积去确定变位参数是不正确的。变位后的高度与变位参数之间存在函数关系,所以应该由高度去求变位参数。

没有变位时,油的体积只与h0有关,是关于h0的一元函数,与α,β变位参数无关。在变位的情况下,观测高度h与α,β变位参数有关,根据变位的几何关系,仅考虑小的变位,容易确定观测高度表达式。对比分析观测高度与实际高度,用数学方法求出α,β。进一步分析得到罐体变位后油位高度间隔为10cm的罐容表标定值。

1 数学建模

1.1 变位前后的油量总体积是不变量

油罐变位后,罐体形状不发生改变。所以在常温常压下,罐体内油的体积不会随变位的改变而改变。所以变位前后的油量总体积是不变量。

1.2 罐内油体积与无变位高度的关系

假设圆柱体半径为a,高为H,左右球半径为r,右球球心为(0,y1,0),左球球心为(0,y2,0),观测点坐标为(0,y0,z0)。模型如图1所示。

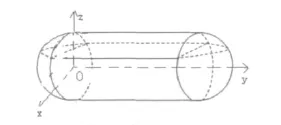
图1 无变位储油罐示意图

右球面方程

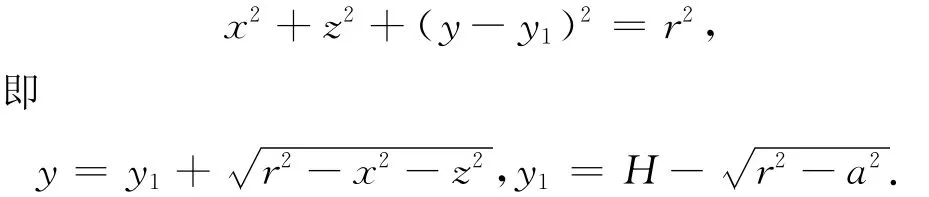
左球面方程

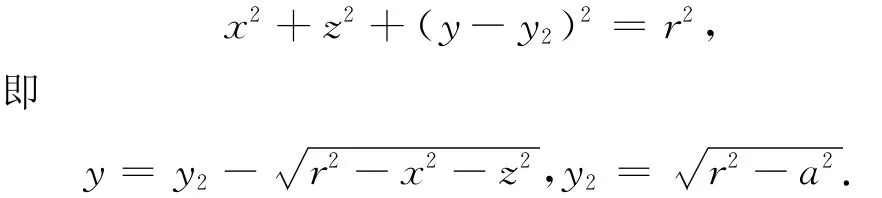
无变位油高h0=z0+a。

无变位时,储油罐油区体积由二重积分可以计算[2]:

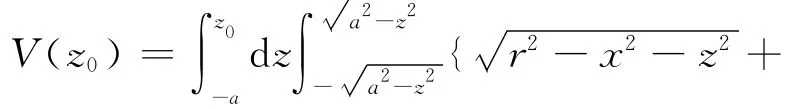
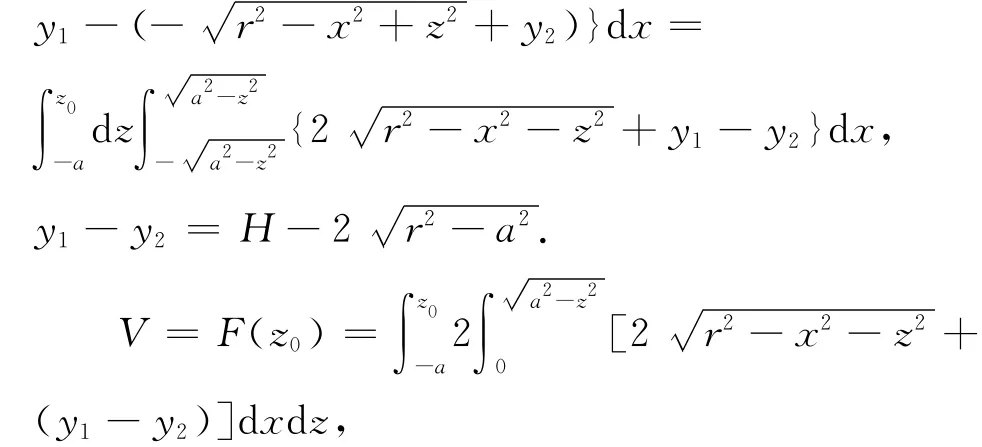
即有

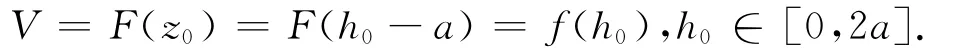
由于此函数是关于h0的单调可微递增函数,必有反函数h0=f-1(V)存在。变位后,假设V= G(α,β,h),由于变位后油高h是h0与变位参数α,β的函数,即

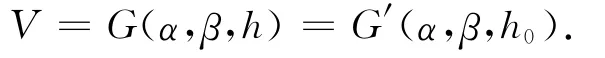
又由变位前后体积不变性可知,

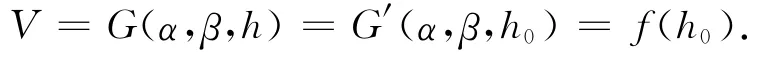
1.3 变位后油高h与h0和α,β的关系式

假设,当只有纵向倾斜时,油罐探针与液面垂直;当只有横向偏转时,探针始终过横向切面圆的圆心。如图2,图3。

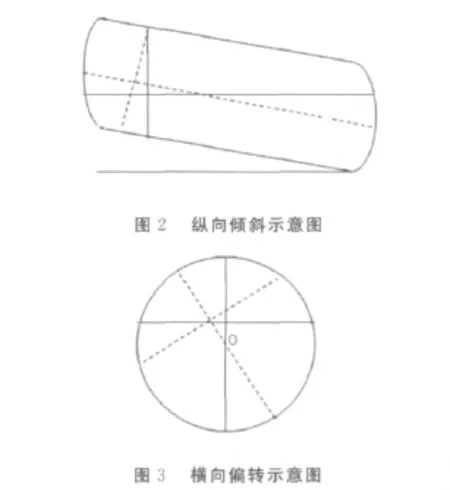
如果无横向偏转,只考虑纵向倾斜,假设|α |≤arctan,根据几何关系可以得到h的函数表达式[3]

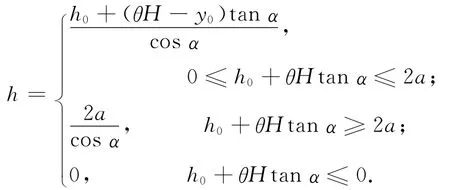
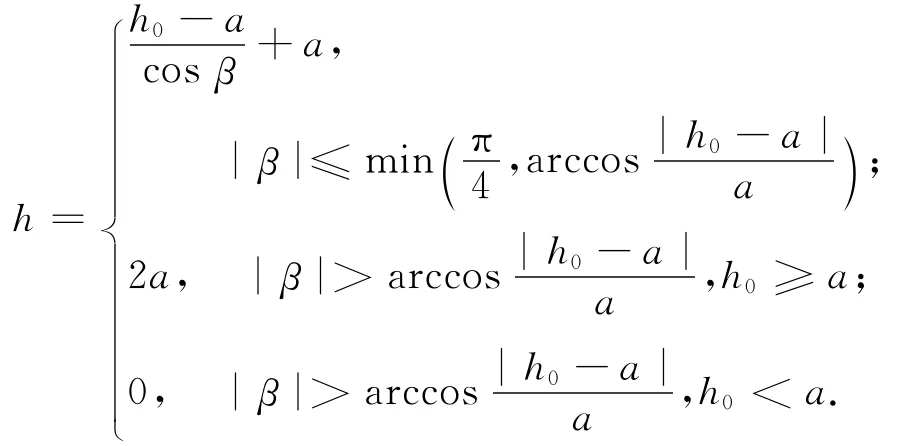
如果考虑纵向倾斜与横向偏转,注意空间几何关系,得到变位后的h和无变位的h0的精确关系式为h=h(h0,α,β)。

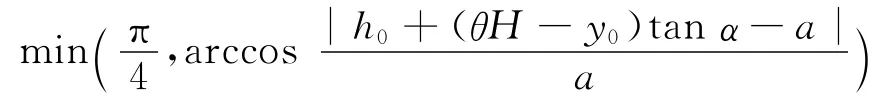
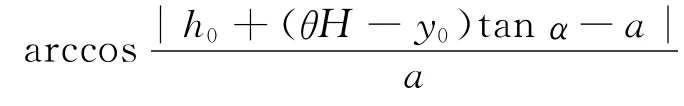
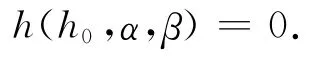
以上式中θH 表示变位前后液面与纵向轴切面交点的y轴坐标。θ是h0的函数,取值范围为(0, 1)。当h0=a时,由变位前后体积不变和模型的空间对称性知,θ=。当h0≠a时,仅考虑微小变位, θ的值变化不大,所以可以假设θ=。

2 数值求解

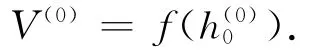
根据实际的第i次出油量ΔVi,确定第i次出油后的油体积为

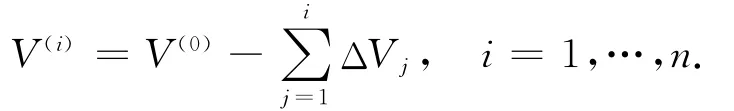
从而得到第i次出油后无变位高度

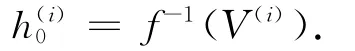
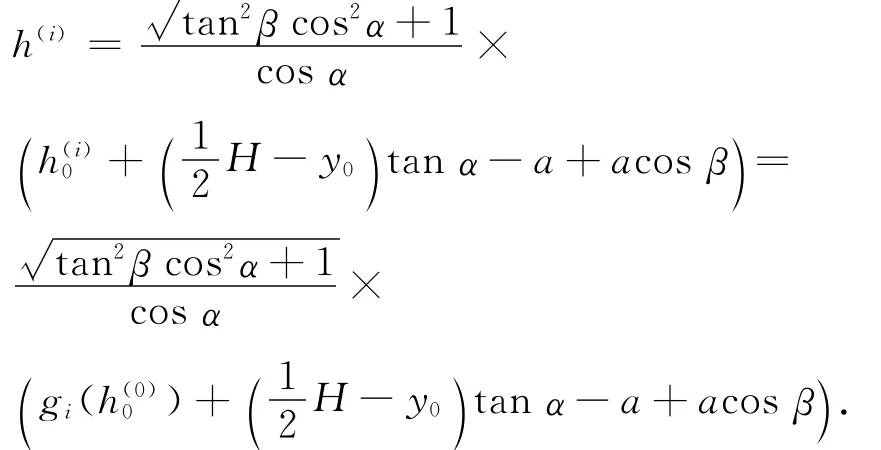
由附件2[1]的检测数据可以知道不同时刻的观测高度实测值h,问题可归结为求解非线性最小二乘问题

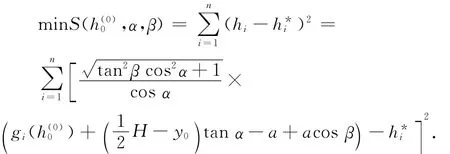
分别取h0=2.5,2.6,2.57。残差比较见表1。

表1 残差比较表

经比较残差,取h0=2.57,此时α=0.032 1, β=0.010 0。

根据上述计算过程,若已知变位后高度,根据变位高度与无变位高度的函数表达式求出对应的无变位高度。然后根据体积表达式即可求出罐内油体积,所以容易得到变位后间隔10cm的体积标定值(见表2)。图4给出了变位前后体积与观测高度的关系。

3 关于2010高教社杯全国大学生数学建模竞赛A题评题要点的意见

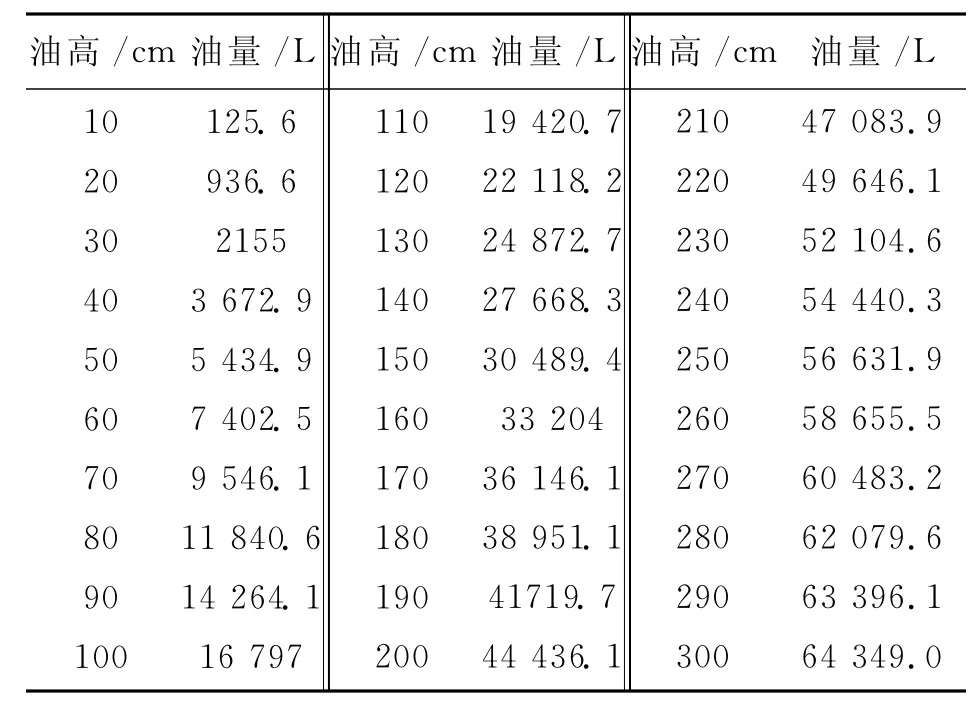
表2 变位后储油罐的修正罐容表

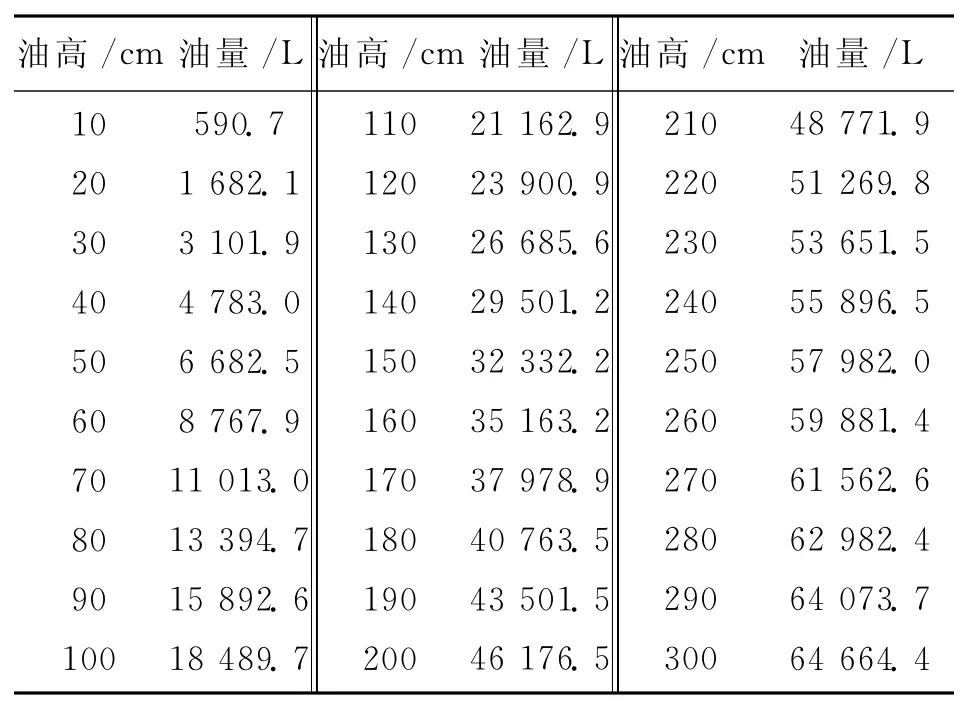
表3 无变位储油罐的修正罐容表

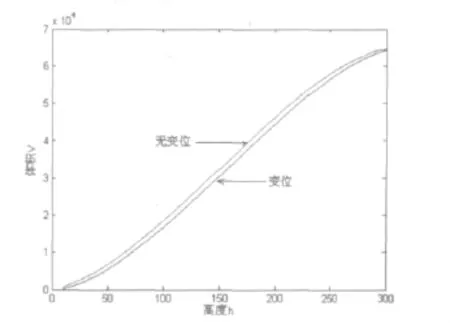
图4 变位与无变位体积对比曲线

2010高教社杯全国大学生数学建模竞赛A题评阅要点中[5],认定罐内实际储油量V与纵向倾斜变位参数α、横向偏转变位参数β和油位高度h的关系模型,即V=F(α,β,h)。由附件2的检测数据可以知道不同时刻的出油量ΔV,同时可以计算出相应油位高度的改变量Δhi=hi-hi+1,并由模型表达式V=F(α,β,h)计算得到实际储油量的改变量ΔVi=F(α,β,hi)-F(α,β,hi+1),问题可归结为求解非线性最小二乘问题:认为利用附件2[1]中的部分数据(如前半部分),借助于工具软件或各种数值方法求解可以得到参数估计值。

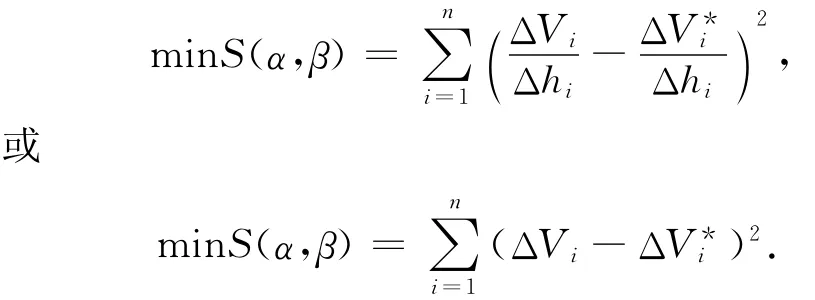
由于变位前后的油量总体积是不变量,且h是h0,α,β的函数,所以h与变位参数α,β是不独立的,而h0,α,β相互独立。所以体积表达式中V=F(α, β,h)应表示为V=F(α,β,h0)。因为体积与变位无关,V=F(α,β,h)=F(0,0,h0)≡f(h0),即体积V=f(h0)只依赖于油的无变位高度h0,与α,β变位参数无关。从而ΔVi=f(h)-f(h),皆与α,β变位参数无关。由min或去确定α,β是错误的,也是不可能的。

[1]2010高教社杯全国大学生数学建模A题[EB/OL]. (2010-09-17).http://www.mcm.edu.cn/html-cn/ node/d5ae730f57dea3208cae73f7635aeee8.html.

[2]华中科技大学数学系.微积分学[M].北京:高教出版社,2002.

[3]吕林根,许子道.解析几何[M].北京:高等教育出版社, 2006.

[4]任玉杰.数值分析及其MATLAB实现[M].北京:高等教育出版社,2007.

[5]2010高教社杯全国大学生数学建模竞赛A题评题要点[EB/OL].(2010-10-01).http://wenku.baidu.com/ view/758edd5f312b3169a451a45c.html.