水下爆炸近场非均熵流的特征线差分解法＊

李晓杰，张程娇，闫鸿浩，王小红，王宇新

（大连理工大学工业装备结构分析国家重点实验室，辽宁 大连116024）

水下爆炸的过程分为炸药的爆轰、冲击波在水中的形成及传播、气体球膨胀收缩运动等3个部分［1］。以往对远场中低压力区的爆炸冲击波和气泡脉动的研究较多，其中远场冲击波压力与气泡脉动压力的测试常被用于炸药爆炸能量评定。对水下爆炸冲击波传播问题的研究通常采用实验和数值模拟的方法。实验测试近场冲击波时，由于冲击波峰值压力可以达到数万至数十万个大气压，冲击波对压力传感器性能要求很高并容易造成严重破坏使得冲击波压力难于测量，因此水下爆炸近场冲击波的实验研究比较困难。近年来对水下爆炸近场问题的研究已逐步采用数值计算的方法解决。目前采用的数值计算方法很多，但本质上仍然是有限差分和有限元2类，采用有限元或高精差分方法模拟冲击波间断问题时，在计算中必须引入人工粘性，对冲击波间断做连续化处理，所计算的冲击波压力受人工粘性系数取值的影响［2－4］。尽管人们已经通过将大量计算结果与实验比较，获得了较合适的人工粘性系数，但人工粘性系数的使用引入了人为干预因素。

特征线差分方法［5］是早期流场计算中常用的一种方法，特征线差分法具有物理概念明确、计算简单、计算精度高等特点。但由于特征线差分法是根据流场全域等熵假定（即均熵假定）获得的，所以只能用于研究均熵流动问题。尽管早期学者也使用特征线法对水下爆炸问题进行过研究，但一直忽略了水下变强度冲击波后的非均熵流特征，而是采用简单的均熵假设来近似处理冲击波问题，这使得特征线差分法计算的正确性受到了质疑。但是特征线差分方法的优点非常明显：（1）无需对冲击波做连续化处理，（2）可以直接将流体的偏微分方程转化为计算精度较高的常微分方程来求解，（3）特征线本身对应着声波的传输轨迹具有明确的物理意义；所以该方法的研究一直受到重视。

本文中从可压缩流的基本方程出发，重新推导含有熵变修正项的2族特征线方程，然后将质点的迹线方程及其能量方程补充为第3族特征线方程，使得特征线方法适用于非均熵流场的求解。而后利用所获得的3族特征线方程组，对质量分数比w（TNT）∶w（RDX）＝40∶60的TNT／RDX球形炸药水下爆炸进行数值计算，并将冲击波近场压力的计算结果与文献［6］中的实验数据进行比较，验证这种改进的特征线差分法的正确性。

1 非均熵流的特征线差分方程

1.1 非均熵流的特征线方程推导

水下爆炸作用时间极短，通常忽略传热效应，视为绝热过程。忽略热传导效应和粘性效应的一维可压缩流的连续方程和运动方程如下

式中：ρ、u、p、r和t分别为流体密度、速度、压强、空间坐标和时间坐标。N＝0，1，2分别表示一维平面、柱面和球面流动问题。以上2式是拉格朗日形式的连续方程和运动方程，也就是沿质点迹线的流动方程。流场内质点的压力可以用熵S与密度ρ来表示p＝p（ρ，S），可以写成

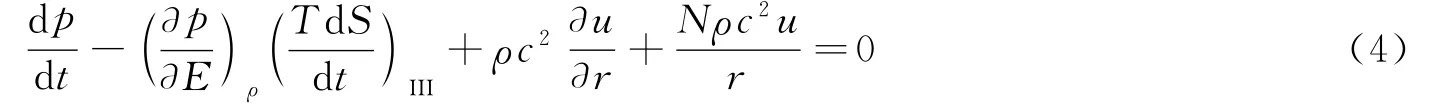
式中：下标III表示物理量沿质点迹线的变化关系，引入系数λ，联立式（4）与式（2）得到

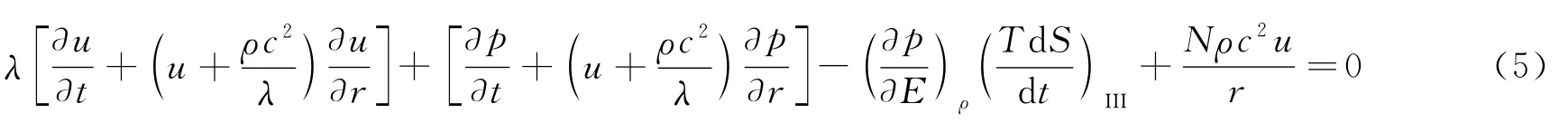
若令λ＝±ρc，那么上式就可以写成

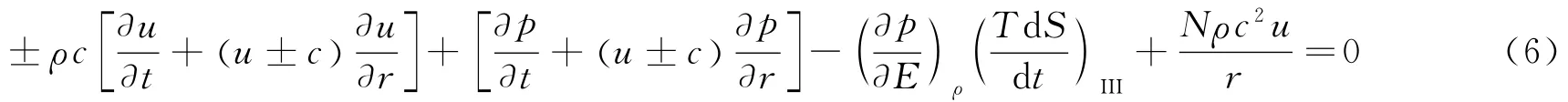
若时空平面内的2族特征线方程为dr／dt＝u±c，代入式（6）就可以获得物理平面上的相容关系，其中右行特征线方程与相容关系如下

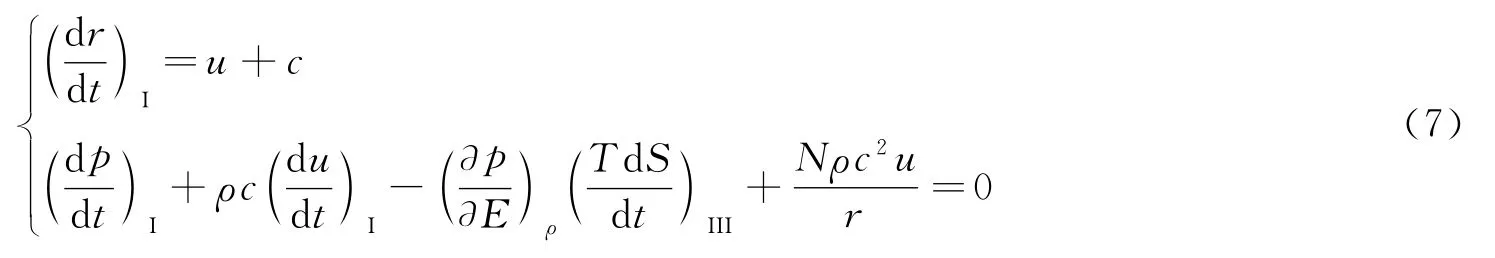
左行特征线方程与相容关系如下

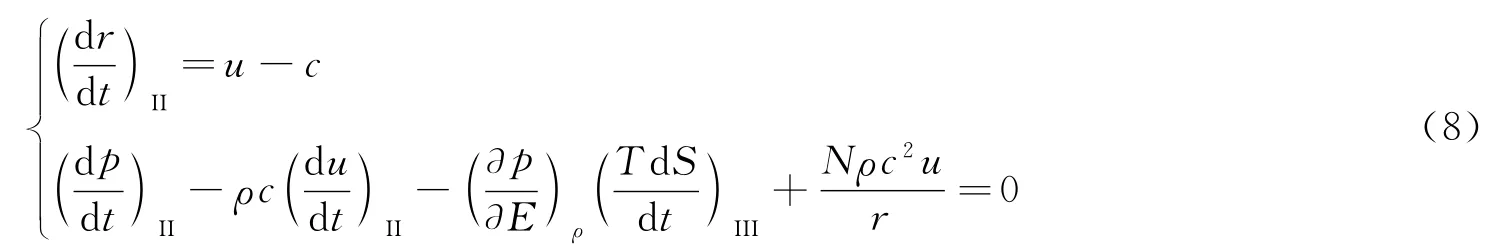
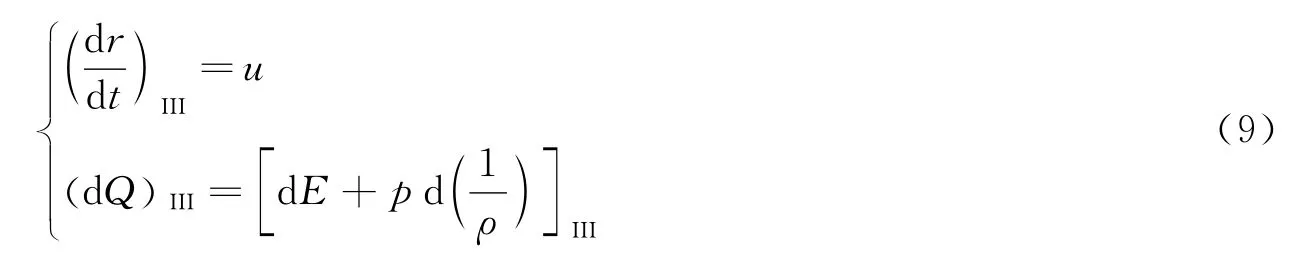
式中：（dQ）III＝（TdS）III，能量方程中显含有熵变项，对于一般问题必须给出熵S的具体表达式。但对于水下爆炸这类高速冲击问题，依然可以假设流体质点之间是绝热的，即每个质点沿迹线是等熵的，但各质点之间的熵变互不相同。因此不要求全流场具有相同的熵变，这就是熵变沿流体质点迹线等熵的全场非均熵流，即（dS）III＝0，因此能量方程就可以写成隐含熵S的形式，即

同样地，由于（dS）III＝0，式（7）、（8）中的项也为0。式（7）、（8）、（10）就构成了可以用于求解非均熵可压缩流的隐含熵S项3族特征线方程。应该注意的是，尽管这3族特征线方程与以往均熵流的方程在形式上几乎完全相同，但所代表的物理意义却完全不同，可以用于处理初始熵变非均匀分布的绝热非均熵流了。例如：对于球对称一维水下爆炸这类变冲击波强度的问题，由冲击波强度确定了波阵面的熵变后，冲击波后方的流场就变成这种沿质点迹线等熵的全场非均熵流场；另外，对于单个冲击波追赶卸载问题也具有同样的特征，也可以化为这类问题用3族特征线方程组求解。

从上述方程可见，在时空平面内，第I、II族特征线方程与标准特征线方程完全相同，均为dr／dt＝u±c；在物理平面内，第I、II族特征线代表了声波小扰动的传播线，推导的特征线方程和标准特征线方程具有相同的物理意义，不同在于推导的相容关系中包含了熵变影响项。这也说明了在任何复杂的流场中，其中任意一点的扰动均会沿着声波小扰动线传播，即第I、II族特征线是物理存在的，而复杂问题在于如何确定特征线上的相容关系。第3族特征线方程组（10）采用了绝热等熵假设，如果使用更复杂的能量方程，该方法可以用于求解带化学反应或带耗散的复杂流动。

1.2 非均熵流的特征线差分格式

在应用标准特征线法求解均熵流场的问题时，只需要前2族特征线就可以求解，其求解方法是用一条右行特征线I与一条左行特征线II相交于某一点，该点的各个参数由这2条特征线所通过的上一时刻的2个节点参数来确定。如图1所示，右行特征线I与左行特征线II相交于A点，A点的各个参数可以用这2条特征线所通过的前一时刻的B、C等2点来求解；如此在给定了计算域初值条件的情况下，就可以求解出域内相关点的参数。标准特征线法求解过程简单并且物理意义明确，然而这种方法是以计算域内流场均熵为基础的，即对均熵流场求解，在计算过程中并未考虑相邻质点间熵值不相等对计算结果的影响。

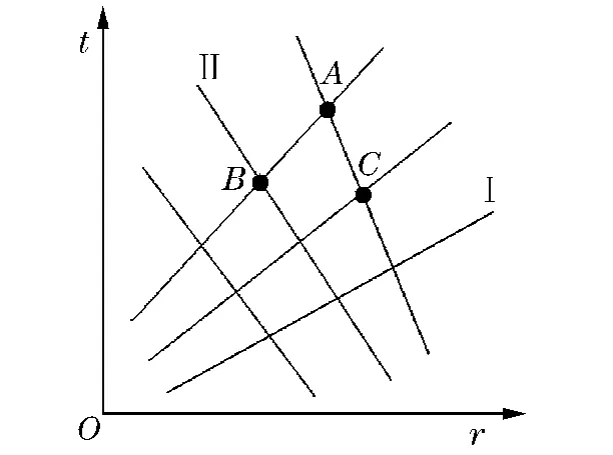
图1 标准特征线法在时空域内的差分方法示意图Fig.1 Standard difference method of characteristics in r－t plane

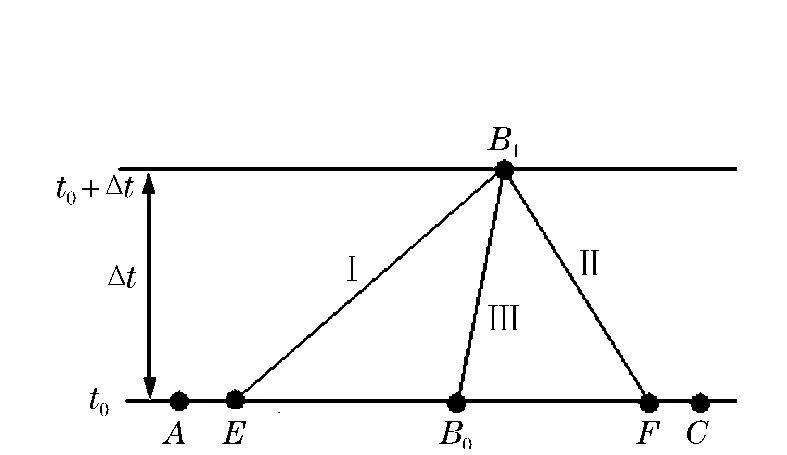
图2 改进的特征线法的差分格式Fig.2 Difference scheme for improved difference method of characteristics

在绝热的流场中，各质点的熵值沿迹线保持不变，本文的特征线方程中添加了熵修正项，并补充加入了质点的迹线方程作为第3族特征线方程，因此可以求解非均熵流场。由于引入了3族特征线也就再无法使用简单的差分方法进行计算了，因此必须使用新的差分方法进行求解。改进特征线法的差分求解方法如下：如图2所示，假定在t0时刻点A、B0、C的参数已知，经过时间Δt，质点由B0沿迹线III运动至B1处，在时空平面上可以沿迹线III求出B1点的坐标；通过B1点的2条特征线I和II又与t0时间线相交于点E和点F，这2点的坐标及各参数可以通过在A、B0与B0、C之间分别插值求得；最后再用点E和点F就可以求出B1点处质点的各个状态参数。若给定初值条件和边界条件，则如此逐层迭代计算就可得出整个域内相关点的参数。

2 水下爆炸近场压力分布的数值计算

一维球面水下爆炸问题是典型的非均熵流问题。爆轰波入射到水中产生球面的水中冲击波，而水中冲击波强度随传播距离增加而不断衰减。由于冲击波引起的熵增与冲击波强度有关，因此水下爆炸冲击波后的熵增也随着传播距离增加而不断减小，所以说球形炸药水下爆炸是典型的非均熵流问题。

2.1 计算模型

将改进的特征线法程序化，对质量分数比w（TNT）∶w（RDX）＝40∶60的TNT／RDX炸药的水下爆炸问题进行数值计算。选用JWL状态方程

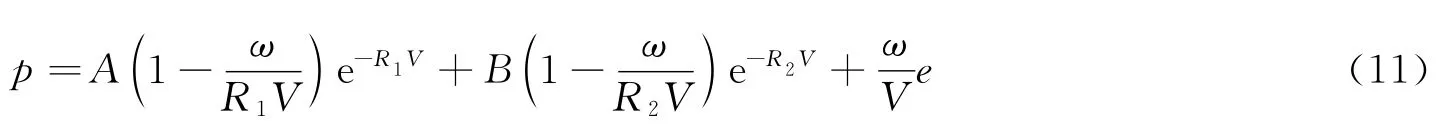
式中：e为单位质量内能；V 为相对体积，V＝v／v0，v0＝1／ρ0，ρ0为炸药初始密度，ρ0＝1.717g／cm3；方程中的其他参数分别取值为：A＝524.23GPa，B＝7.678GPa，R1＝4.2，R2＝1.1，ω＝0.34；炸药爆速D＝7.98km／s。

对水选用多项式形式的状态方程，当水受压和膨胀时，有

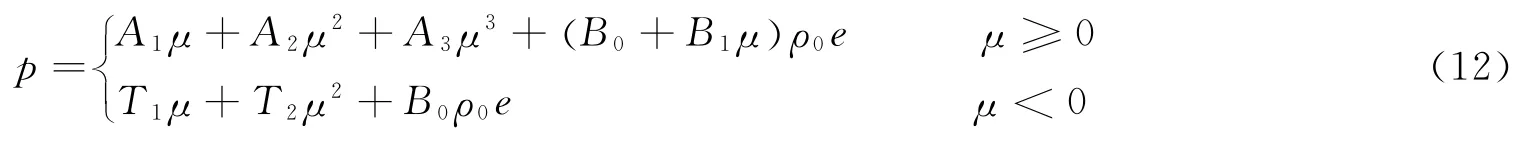
式中：μ 是压缩度，μ＝ρ／ρ0－1；e是单位质量内能；ρ0是初始密度，ρ0＝1.0g／cm3；方程中的其他参数：A1＝2.2GPa，A2＝9.54GPa，A3＝14.57GPa，T1＝2.2GPa，T2＝0，B0＝0.28，B1＝0.28。

计算中采用一维球对称模型，在无限水域中放入1kg的质量分数比w（TNT）∶w（RDX）＝40∶60的TNT／RDX炸药球，药球半径为5.18cm。为了避开药球中心处的计算奇点，起爆点设置在距离球心0.2cm的球面上，起爆后在该处设置固壁边界条件；网格大小设置为0.249cm，炸药内划分20个网格。

2.2 计算结果

数值计算结果如图3所示，图中绘制出了1≤R／R0≤4范围内的峰值压力pmax－比例距离R／R0的曲线。为检验本文中提出的改进的特征线法，将计算结果与池家春等［6］的实验结果进行了比较，实验值公式如下

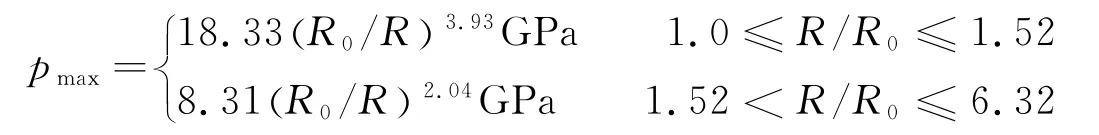
从图3中可以看出，冲击波峰值压力的计算值与实验值符合较好。在比例距离1≤R／R0≤4的近场范围内，两者最大相对误差为13.1%，这说明本文的特征线法完全可以用于处理水下爆炸近场的非均熵流问题。

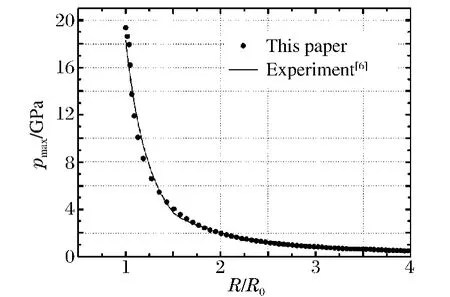
图3 近场冲击波峰值压力的比较Fig.3 Comparison of the peak pressures in the near－field region

3 结 论

本文中提出了一种改进的特征线法，在特征线方程中添加了熵的修正项，并将质点的迹线作为第3族特征线加入到特征线方程组中，使它可以用于求解变强度冲击波及波后的非均熵流场。由于时空平面内的第I、II族特征线与标准特征线方程在形式上完全相同，因此非均熵流的前2族特征线方程同样也代表了声波小扰动的传播线，与标准特征线方程具有相同的物理意义。

将改进的特征线法程序化，对质量分数比w（TNT）∶w（RDX）＝40∶60的TNT／RDX炸药球的水下爆炸问题做了计算。在比例距离1≤R／R0≤4的近场范围内，用本文的特征线法计算得到的冲击波峰值压力与实验值［6］最大误差为13.1%，从而验证了非均熵特征线法的正确性。另外，这种方法无需采用人工粘性系数处理冲击波间断，只需给定计算所需的相关物理参数即可求解，因此减少了对冲击波的人为干预因素。

［1］Cole R H.Underwater explosions［M］.New Jersy：Princeton University Press，1948：3－13，110.

［2］刘科种，徐更光，辛春亮，等.AUTODYN水下爆炸数值模拟研究［J］.爆破，2009，26（3）：18－21.LIU Ke－zhong，XU Geng－guang，XIN Chun－liang，et al.Research on numerical simulation in underwater explosioln by AUTODYN［J］.Blasting，2009，26（3）：18－21.

［3］徐豫新，王树山，李园.水下爆炸数值仿真研究［J］.弹箭与制导学报，2009，29（6）：95－97，102.XU Yu－xin，WANG Shu－shan，LI Yuan.Study on numerical simulation of the underwater explosive［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2009，29（6）：95－97，102.

［4］方斌，朱锡，张振华，等.水下爆炸冲击波数值模拟中的参数影响［J］.哈尔滨工程大学学报，2005，26（4）：419－424.FANG Bin，ZHU Xi，ZHANG Zhen－hua，et al.Effect of parameters in numerical simulation of underwater shock wave［J］.Journal of Harbin Engineering University，2005，26（4）：419－424.

［5］Chou P C，Huang S L，Karpp R R.Numerical calculation of blast wave by the method of characteristics［J］.AIAA Journal，1967，5（4）：618－623.

［6］池家春，马冰.TNT／RDX（40／60）炸药球水中爆炸波研究［J］.高压物理学报，1999，13（3）：199－204.CHI Jia－chun，MA Bing.Underwater explosion wave by a spherical charge of composition B－3［J］.Chinese Journal of High Pressure Physics，1999，13（3）：199－244.