水下爆炸载荷作用下环肋加筋圆柱壳结构的弹塑性动力屈曲＊

袁建红，朱 锡，张振华

（海军工程大学船舶与动力学院，湖北 武汉430033）

舰船结构受到水下爆炸载荷作用时会产生严重的瞬态突加载荷的作用，在动压力的作用下，不仅板架中的板和骨架可能发生局部塑性变形，而且在载荷足够大时，板和骨架等结构可能产生失稳。以往，在确定船体结构（梁、板以及板架）的临界失稳载荷时，都是按照静力屈曲理论来处理。实际上，船体结构在冲击载荷作用下会呈现比静态高很多的屈曲波数，临界屈曲载荷也高于静态屈曲载荷，应变率效应及载荷的历史对屈曲有重要影响。采用适合水下爆炸的动力屈曲理论来确定船体结构动承载能力将更加合理准确。

潜艇受水下爆炸动力屈曲可简化为两端固定有限长圆柱壳受径向冲击的塑性动屈曲问题［1］。鉴于它的军事敏感性，公开报道的有关文献很有限。W.S.Strickland等［2］报道过圆柱壳屈曲的系列实验结果，永井保［3］则进行了系列水下爆炸试验。S.W.Kirkpatrick等［4］采用数值方法讨论了圆柱壳结构的不对称屈曲问题。通常人们研究简化了的情形，如结构的响应是纯塑性或纯弹性的，外载荷通常被简化为初速度并沿周向均布。实际中存在很多不对称屈曲问题，许多壳体处于中等厚度范围，它们通常呈现出弹塑性动力屈曲，应变率反号也需考虑。由于理论上的难度，处理这类问题只能借助于数值分析。随着有限元软件的逐渐成熟，用数值分析方法对复杂结构的屈曲问题分析已成为可能。为了确定动力屈曲的临界屈曲载荷和屈曲时间，需要采用相适应的动力屈曲准则。目前已经提出了一些动力屈曲判定准则，这些屈曲准则各有优缺点和一定适用范围。其中Budiansky－Roth准则建立在物理直观上，且很容易在数值计算中实现，已经得到了广泛的应用［5－10］。

本文中应用MSC－DYTRAN数值分析软件建立加筋圆柱壳结构流固耦合的系列分析算例，讨论更为一般的情况，即载荷是随时间变化的冲击波，用数值分析方法对加筋圆柱壳在爆炸冲击波作用下的弹塑性动力屈曲问题进行研究。应用Budiansky－Roth准则和Southwell方法确定结构的动力屈曲临界载荷；讨论了水下爆炸载荷作用下加筋圆柱壳弹塑性动力屈曲的影响因素（载荷强度、网格密度、径厚比、长径比、加筋间距、加筋尺寸等）对加筋圆柱壳结构动屈曲模态和临界屈曲载荷的影响。

1 有限元模型

1.1 模型描述

加筋圆柱壳模型取自文献［6］，如图1所示，其中x为轴向距离，L为舱段长度，R为圆柱壳体半径，t为圆柱壳板厚度，水域网格最小单元尺寸为0.1m。为了分析网格尺寸、径厚比、长径比、加筋间距及加筋截面尺寸的影响，设计了一系列算例，基本参数如表1所示。ΔL为圆柱壳结构网格单元最小尺寸，h为加筋高度，b为加筋厚度，n为加筋数，加筋圆柱壳端部约束为固定支撑，欧拉水域尺度为6m×6m×8m。TNT药包位于模型跨中正下方。

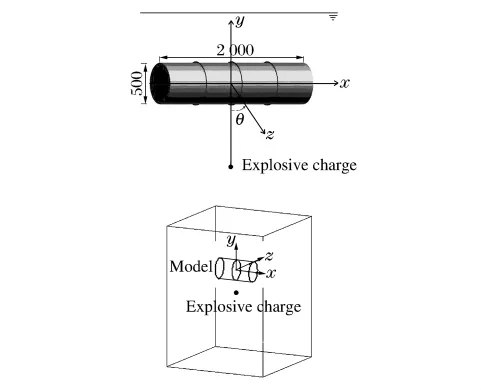
图1 加筋圆柱壳模型Fig.1 The model of ring－stiffened cylindrical shell

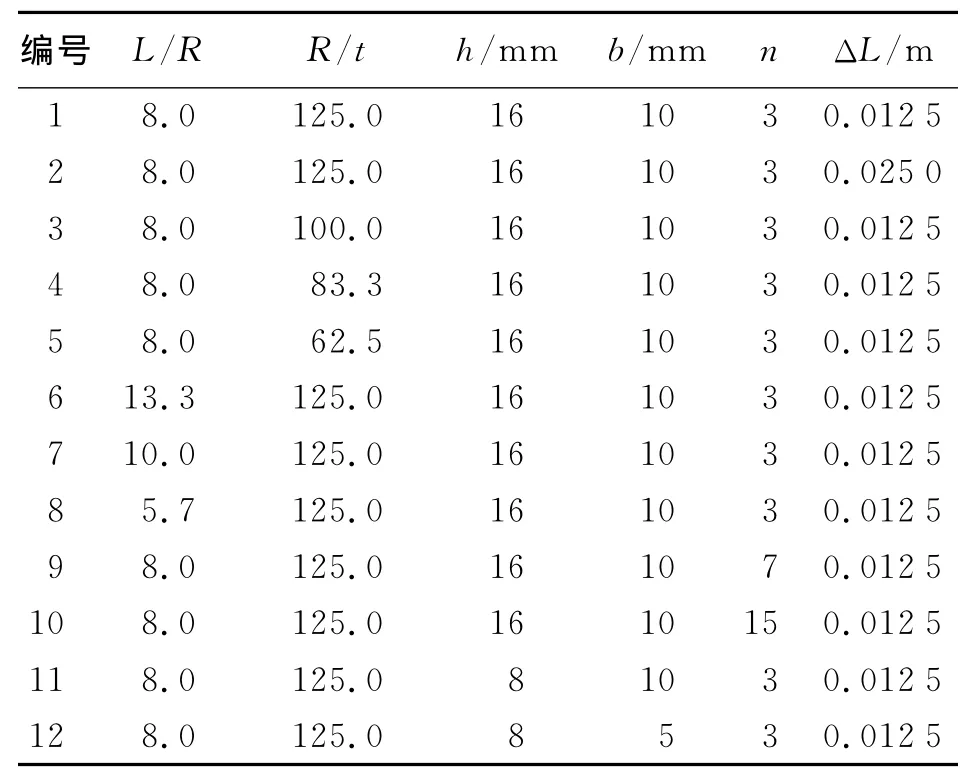
表1 加筋圆柱壳算例的基本参数Table 1 Parameters of ring－stiffened cylindrical shell

1.2 材料参数选取

加筋圆柱壳结构在水下爆炸载荷作用下弹塑性响应是一个动态响应过程，动力影响不能忽略，由于船用低碳钢的塑性性能对应变率高度敏感，其屈服应力和拉伸强度极限随应变率增加而增加，故在材料算例中引入应变率敏感性的影响。本文中采用与实验数据符合较好的Cowper－Symonds本构方程［11］

式中：σD为动屈服应力，σ0为相应的静屈服应力，ε为应变率，D和P为对于具体材料而言为常数，对于低碳普通船用钢：σ0＝235MPa，D ＝40.4和P＝5。

1.3 状态方程选取

炸药的状态方程采用JWL方程来描述

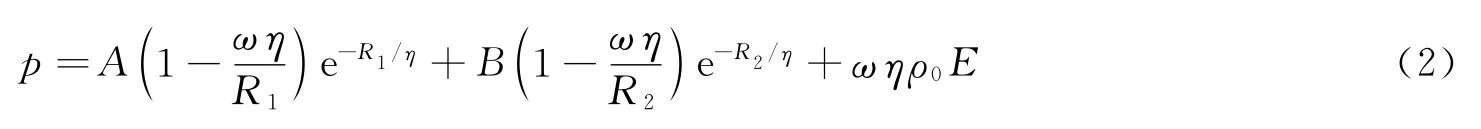
式中：η＝ρ／ρ0，ρ0为材料的参考密度，ρ 为材料总体密度，E 为单位质量的内能，A、B、R1、R2和ω 为JWL状态方程的5个待定参数。对于标准炸药 TNT，A＝3.712×1011，B＝3.231×109，R1＝4.5，R2＝0.95，ω＝0.30，材料的参考密度ρ0＝1 580kg／m3，E＝4.19MJ／kg。

水下冲击波的压力值一般在115～215GPa，属于中等强度冲击波，这时冲击波通过介质后熵值变化很小，一般可以认为是等熵过程，水介质的等熵状态方程为

为了便于 MSC－DYTRAN程序应用，将其变换为多项式形式p＝a1μ＋a2μ2＋a3μ3，μ＝ρ／ρ0－1，其中a1＝2.18×109，a2＝6.69×109，a3＝1.15×1010，水的初始密度ρ0＝1 000kg／m3，空化压力设为0。

2 动力屈曲准则

要获得结构的动力屈曲、屈曲模态、临界屈曲载荷和屈曲时间这些特征量，必需制定动力屈曲判定准则。Budiansky－Roth准则是建立在物理直观上，通过运动方程直接求解位移和载荷关系。当受冲击的球壳结构在微小载荷增量下引起剧烈响应，所对应的载荷定义为临界载荷。B－R准则容易在数值计算中实现，因而得到广泛的应用。如何度量所谓的“微小载荷增量下引起剧烈响应”，文献［12］中指出当结构初始缺陷较小时，位移载荷曲线存在一个位移变化显著的区域，这时B－R准则适用，而当结构初始缺陷较大时，位移载荷曲线不存在一个位移变化显著的区域，这时B－R准则不再适用。I.Ellishakoff［13］提出了基于B－R准则的广义B－R屈曲准则，即认为当位移达到某个规定的临界值时则冲击屈曲发生。

对于柱、板一类具有稳定后屈曲路径的结构，Southwell方法是一种简便，直观而又可靠的确定结构临界屈曲载荷的方法。本文中选取爆炸载荷作用下加筋圆柱壳最大径向位移值为分析对象，定义量纲一载荷参数p＝pm／p0，其中，pm为爆炸载荷冲击波峰值，p0为加筋圆柱壳结构承受均匀径向压力时壳板静力失稳临界压力；定义结构弹塑性响应的量纲一位移参数w＝wm／t，其中，wm为爆炸载荷作用下加筋圆柱壳径向位移的最大值，t为壳板厚度，通过数值分析可以得到w随p变化的关系曲线，应用B－R准则和Southwell方法来确定加筋圆柱壳屈曲临界载荷pcr。

3 影响因素分析

3.1 爆炸载荷强度影响

针对算例1，保持其它参数不变，通过改变爆距设置7个计算工况，得到如图2所示的加筋圆柱壳径向位移随冲击波压力峰值的变化曲线。图2（a）中显示随着爆炸载荷的增大加筋圆柱壳最大径向位移开始增长缓慢，随后最大径向位移增长速度明显加快，应用B－R屈曲准则确定加筋圆柱壳结构的临界动力屈曲载荷p＝8.58。将量纲一载荷峰值与量纲一最大径向位移的关系采用Southwell方法处理得到的直线如图2（b）所示，该直线斜率的倒数即为该结构的屈曲临界载荷为p＝9.17，用B－R屈曲准则和Southwell方法确定的屈曲临界载荷误差约为4.4%，因此这2种方法确定的屈曲载荷相一致。

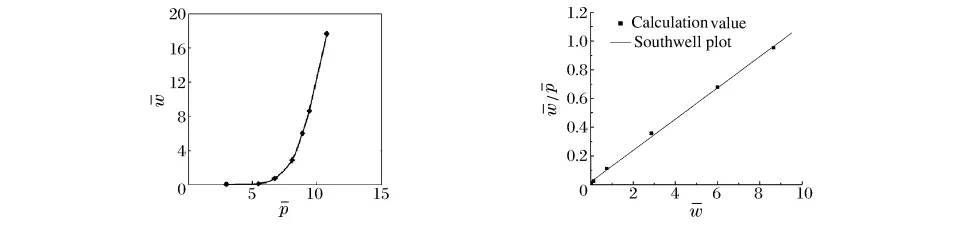
图2 加筋圆柱壳径向位移随相关参数的变化曲线Fig.2 The curves of the maximum radial displacement versus the relative parameter

3.2 模型参数影响

3.2.1 网格密度影响

图3给出了算例1在TNT药量为0.389kg、爆距1.8m爆炸计算工况下τ＝1，2，3ms时刻典型截面（x＝L／8）的径向位移沿周向分布曲线，图中显示随着时间增长，加筋圆柱壳在肋间沿轴向形成一个半波，沿周向呈现出多个屈曲波纹，屈曲波纹主要集中在迎爆面和侧爆面，并且屈曲程度随时间增长逐渐加大，屈曲范围具有沿周向逐渐扩大至整个圆柱壳的趋势，这说明屈曲的传播非常迅速，屈曲幅值具有随着θ增加而减小的趋势，这与爆炸载荷随着θ增加而减小的分布规律相一致。

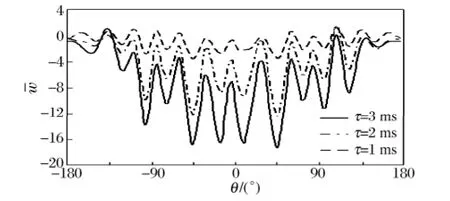
图3 算例1典型横剖面径向位移沿周向分布曲线Fig.3 The curves of radial displacement versus circumferential angle at typical transverse section

图4给出了τ＝10ms时刻不同网格密度的加筋圆柱壳弹塑性响应对比，2个算例的主要差别是算例2的Lagrange最小单元尺寸为算例1的2倍。图4表明2个算例的屈曲模态有较大差异，算例1得到的屈曲波纹数高于算例2，且结构的最大径向位移也高于算例2，这是由于较粗的网格划分会使模型过于刚硬，从而导致在同样爆炸载荷作用下粗网格模型的动力屈曲发展有所减弱。可得出结构的网格划分密度对结构的动力屈曲比较敏感。选择较粗的网格会得到比实际情况高的动力屈曲临界载荷。因此要想获得接近实际的屈曲模态和临界载荷，可靠的做法是基于实验中的屈曲形状进行数值模拟以确定适宜的网格划分，采用文献［4］网格划分建议值，取每个屈曲波长上的网格数不小于10。

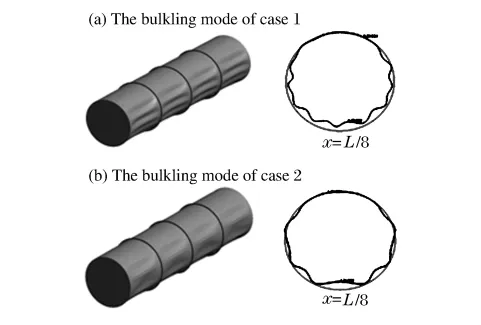
图4 不同网格密度的加筋圆柱壳弹塑性响应对比Fig.4 Dynamic response of structure with different Lagrange meshes

3.2.2 径厚比影响

保持其他计算参数不变，通过改变径厚比设置4个工况，设计径厚比R／t分别为125、100、83和62.5的算例1、3、4、5。

图5为相同工况下τ＝10ms时刻不径厚比加筋圆柱壳典型剖面径向位移沿周向分布图，图中显示随着径厚比的增加，加筋圆柱壳肋间壳板的屈曲有明显增强的趋势，并且随着屈曲波数逐渐增多，屈曲范围沿周向有逐渐向整个壳体迅速扩展的趋势。

图5 加筋圆柱壳径向位移沿周向分布曲线Fig.5 The curves of radial displacement versus circumferential angle at typical transverse section

对这几个算例进一步分析，得到不同径厚比的加筋圆柱壳径向位移与爆炸载荷的关系曲线图6（a），应用B－R准则和Southwell方法确定临界屈曲载荷值，将临界屈曲载荷值与径厚比的关系绘入图6（b）中，图中显示随着径厚比的减小，结构的临界屈曲载荷呈现出基本线性增加的趋势，当径厚比从125减小至83时，即减小约为33.6%，动屈曲临界屈曲载荷大约增加为40%，当径厚比从125减小至62.5时，即减小约为50%，动屈曲临界屈曲载荷大约增加为56%，由此可见加筋圆柱壳的响应对径厚比非常敏感；因此要提高加筋圆柱壳的抗动力屈曲能力，应当选择适当的径厚比。

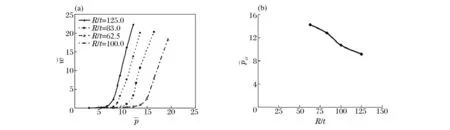
图6 不同径厚比加筋圆柱壳径向位移与爆炸载荷的关系曲线Fig.6 The curves of the maximum radial displacement versus explosive load with different radius－to－thickness ratios

3.2.3 长径比的影响

保持其他计算参数不变，设计长径比分别为L／R＝13、10、8、5.7的计算算例1、6、7、8。

对这几个算例进行分析，计算显示在相同爆炸载荷作用下，随着长径比的减小，加筋圆柱壳结构的最大径向位移减小，屈曲波纹数基本保持不变。进一步计算得到不同长径比的加筋圆柱壳径向位移与爆炸载荷的关系曲线图7（a），应用B－R准则和Southwell方法确定临界屈曲载荷值，将临界屈曲载荷值与径厚比的关系绘入图7（b）中，图中显示随着长径比的减小，临界爆炸屈曲载荷呈现出缓慢增加的趋势，当长径比从8减小至5.7时，即减小约29%时，临界爆炸屈曲载荷增大约为4%；当长径比从8增加至13.3时，即增加约66%时，临界爆炸屈曲载荷减小约为9%。由此可以看出，随着长径比的减小，结构的抗动力屈曲能力略有增强，但是增长的幅度不及结构径厚比的影响显著。

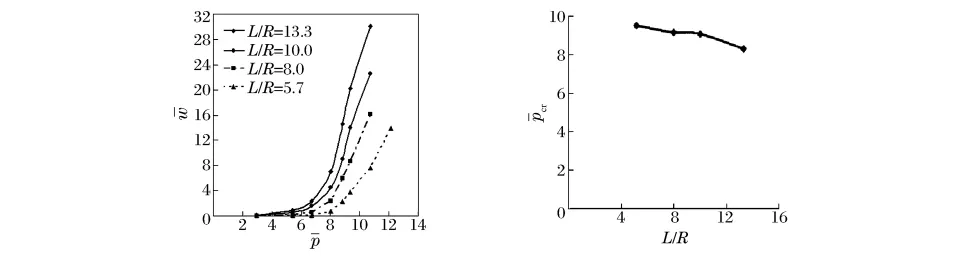
图7 不同长径比加筋圆柱壳结构径向位移与爆炸载荷的关系曲线Fig.7 The curves of the maximum radial displacement versus explosive load with different ratio of length to radius

3.2.4 加筋数影响

保持加筋截面尺寸不变，通过改变加筋间距设计了加筋数分别为3、7和15的3个算例。

计算表明在相同爆炸载荷作用下，不同加筋数的结构屈曲模态及周向屈曲波数基本相同，随着加筋数的增加，结构的最大径向位移显著减小；对这3个算例进一步计算得到不同加筋数圆柱壳径向位移与量纲一水下爆炸载荷的关系曲线如图8所示，图中表明随着加筋数的增加使得结构抗动力失稳的能力增强，当加筋间距减小50%时，即加筋数由3根增加至7根时，临界爆炸屈曲载荷增加约为15%，当加筋间距减小75%时，即加筋数由3根增加至15根时，临界爆炸屈曲载荷增加约为45%。

3.2.5 加筋截面尺寸影响

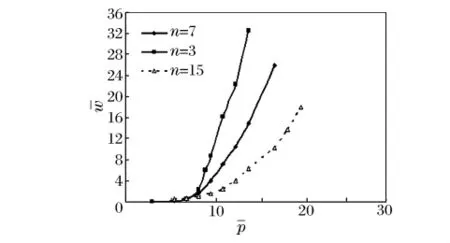
图8 不同加筋数加筋圆柱壳径向位移与爆炸载荷关系曲线Fig.8 The curves of the maximum radial displacement versus explosive load with different ribs number

保持加筋数不变，改变加筋截面尺寸，设计了加筋截面面积（h×b）分别为16mm×10mm、8mm×10mm和8 mm×5mm的3个算例。由图9（b）可以看出，当加筋面积减少为原来的一半时，不仅加筋圆柱壳的肋间壳板发生明显的局部失稳模态，中部加筋同时也呈现屈曲现象，而加筋圆柱壳算例1仅仅出现了筋间壳板的局部失稳，并且其屈曲程度不及后者剧烈。

图9 不同加筋截面尺寸的加筋圆柱壳结构弹塑性响应对比Fig.9 Buckling mode of structure with different section size of ribs

对这3个结构进一步计算分析得到了不同加筋截面面积的加筋圆柱壳x＝0和x＝L／8剖面最大径向位移与爆炸载荷的关系曲线如图10所示，图10（a）中显示随着加筋截面尺寸的减小加筋刚度减小，加筋结构的抗动力失稳能力明显削弱，当截面面积由16mm×10mm减小为8mm×10mm，即剖面积减小约50%时，临界动屈曲载荷减少约为22%。图10（b）显示加筋截面面积对加筋间壳板局部抗动力屈曲能力影响较小。

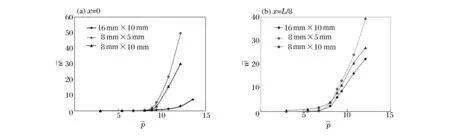
图10 不同肋骨尺寸的加筋圆柱壳径向位移与爆炸载荷的关系曲线Fig.10 The curves of the maximum radial displacement versus explosive load with different section size of ribs

4 结 论

通过对以上典型加筋圆柱壳结构在水下爆炸载荷作用下的动力响应和屈曲分析，得出了如下结论：

（1）采用本文中建立的流固耦合有限元分析模型，应用动力瞬态有限元软件MSC－DYTRAN能够对典型加筋圆柱壳结构的径向非对称屈曲现象进行数值模拟，较粗的网格划分通常会得到比实际情况高的动力屈曲临界载荷，结果的精度有赖于选择合适的结构网格尺寸和关键参数。

（2）加筋圆柱壳结构的最大径向位移与水下爆炸载荷的关系曲线没有呈现出明显的拐点，应用Budiansky－Roth准则和Southwell方法仍然可以来确定结构的动力屈曲临界载荷以便工程应用。

（3）结构的径厚比对动力屈曲临界载荷的影响最为敏感，随着径厚比的减小，结构的临界屈曲载荷呈现出明显增加的趋势。

（4）长径比、加筋数、加筋截面尺寸对动力屈曲临界载荷的影响较小。长径比越大，结构动力屈曲的临界载荷越小；加筋数越多，结构动力屈曲临界载荷越大；加筋截面尺寸面积越大，结构动力屈曲临界载荷越大。

［1］顾王明.冲击及流－固冲击载荷作用下圆柱壳的非弹性动力屈曲研究［D］.武汉：华中科技大学，1993：60－70.

［2］Strickland W S，Milton J E，Ross C A，et al.Failure of aluminum cylindrical shells subjected to transverse blast loadings［J］.Shock Vibration Bull，1977，47（4）：111－120.

［3］永井保.円筒壳の冲击外力による局部凹损试验の結果について［C］∥日本造船协会论文集.1966：108－115.

［4］Kirkpatrick S W，Holmes B S.Structural response of thin cylindrical shells subjected to impulsive external loads［J］.AIAA Journal，1988，26（1）：96－103.

［5］李荣富，程远胜，汪玉，等.爆炸冲击载荷下耐压鞍型舱壁结构弹塑性动力屈曲［J］.振动与冲击，2009，28（9）：139－142.LI Rong－fu，CHENG Yuan－sheng，WANG Yu，et al.Elastic－plastic dynamic buckling of a saddle－shaped bulkhead under blast impact loading［J］.Journal of Vibration and Shock，2009，28（9）：139－142.

［6］余晓菲.加筋圆柱壳在水下爆炸载荷作用下的动力响应及动力屈曲［D］.华中科技大学.2007.

［7］刘理，刘土光，李天匀.轴向冲击载荷下圆柱壳的弹塑性屈曲分析［J］.爆炸与冲击，2000，20（2）：168－174.LIU Li，LIU Tu－guang，LI Tian－yun.Buckling of cylindrical shells under axial impact［J］.Explosion and Shock Waves，2000，20（2）：168－174.

［8］徐加初，杨增涛.爆炸冲击下复合材料层合扁球壳的动力屈曲［J］.爆炸与冲击，2007，27（2）：116－120.XU Jia－chu，YANG Zeng－tao.Dynamic buckling of laminated composite shallow spherical shells subjected to explosive impact［J］.Explosion and Shock Waves，2007，27（2）：116－120.

［9］Jabareen M，Sheinman I.Buckling and sensitivity to imperfection of conical shells under dynamic step－loading［J］.Journal of Applied Mechanics，2007，74（1）：74－80.

［10］Kubiak T，Kolakowski Z，Kowal－michalska K.Dynamic response of conical and spherical shell structures subjected to blast pressure［C］∥SDSS’Rio 2010Stability and Ductility of Steel Structures，2010：1192－1200.

［11］陈志坚，袁建红，赵耀，等.C－S模型参数及对非接触爆炸仿真分析的影响研究［J］.振动与冲击，2008，27（6）：60－63.CHEN Zhi－jian，YUAN Jian－hong，ZHAO Yao，et al.The C－S parameter and its effect on simulation of non－contact explosion problems［J］.Journal of Vibration and Shock，2008，27（6）：60－63.

［12］王德禹.受静载作用的直杆在周向冲击载荷下的屈曲［J］.振动与冲击，1997，16（1）：35－37.WANG De－yu.Buckling of a statically pre－loaded column under axial impact load［J］.Journal of Vibration and Shock，1997，16（1）：35－37.

［13］Elishakoff I.Axial impact buckling of a column with random initial imperfections［J］.Journal of Applied Mechanics，1978，45：361－365.