炸药性质对岩石粒子运动影响的数值模拟＊

覃剑锋，焦清介，聂建新

（北京理工大学爆炸科学与技术国家重点实验室，北京100081）

炸药爆炸后在岩石介质内激起应力波是造成岩石破坏的一个重要因素［1］。应力波的传播和衰减，同时造成裂纹的形成和扩展以及表面抛掷成坑等现象，所以岩体介质中的应力波传播和衰减特性是岩石爆破理论的重要组成部分。由于实验条件的限制，难以进行大量的爆破实验，随着计算机水平的发展，数值模拟已成为研究这类复杂问题的手段之一［2－4］。但是数值模拟结果的可靠性需要实验来验证，所以实验也是不可缺少的。岩石介质内应力波压力的直接测试多采用压阻法［5－6］和压电法［7］，岩体性状和环境条件对测试精度的影响很大，结果离散型较大，不易处理和分析。应力波引起岩石粒子的扰动，所以粒子运动特性也能反映应力波的特性，而且对于粒子运动参量的测量，测试技术相对完善，受环境干扰小，所以可选择对粒子的运动规律进行分析。J.K.Gran等［7］、王占江等［8－9］用圆环形电磁粒子速度计测得了爆炸载荷下花岗岩和混凝土中的粒子速度，实验重复性较好。

虽然针对岩石介质中应力波的传播和衰减规律做了大量研究，但大多集中在对不同岩体和爆破条件下的分析。对炸药的处理较为简单，通常是将不同炸药以爆热作为等效参量进行等效［10］，仅考虑了爆热的影响，而炸药种类以及非理想炸药的能量释放速率等对介质中爆炸应力波影响的研究较少。不同的炸药具有不同的爆压和爆速以及爆轰产物的膨胀特性，其中爆压和爆速是影响岩石中入射应力波的因素［1］，爆轰产物的膨胀特性影响能量的传递，爆炸释放的能量以应力波的形式在介质中传播，能量释放的快慢也会影响传递给介质的能量，从而影响应力波的传播。所以研究炸药种类，能量释放速率等因素对岩石中爆炸应力波的影响规律，可为工程实践中炸药的选取提供参考依据。

本文中，利用AUTODYN［11］软件模拟炸药在花岗岩中的爆炸过程，结合实验结果，分析介质中粒子的运动规律，并着重研究炸药性质对粒子运动参数的影响。

1 模型的建立

1.1 物理模型和计算模型

在圆柱形蓝田花岗岩试件中装有球形炸药PETN，密度为1 500kg／m3，半径2.5mm，质量为0.125g。爆炸试件尺寸远大于装药半径，可忽略边界效应对粒子运动的影响，图1为模型的剖面图。装药中心起爆，在壁面上激起球面入射应力波并在岩石介质中传播。

物理模型具有对称性，用二维轴对称算法，以减少网格数量，提高计算效率，计算模型如图2所示。岩石介质用拉格朗日网格描述，炸药爆炸后产物剧烈膨胀，建立欧拉网格使炸药产物在网格间自由流动。岩石和炸药网格间定义流固耦合算法。x轴为默认的对称轴，y轴方向上需定义对称边界，在炸药中心设置起爆点。沿x轴方向上设置计算点，可记录各点上的运动曲线。计算点1设置在炸药与岩石界面处，计算点2距离装药中心10mm，2～13等间距布置，间距为10mm。

图1 物理模型Fig.1 Physical model

图2 计算模型Fig.2 Simulation model

1.2 材料模型

材料力学行为的准确描述是保证数值模拟精度的前提，模型中涉及到2种材料：炸药和岩石。

1.2.1 炸 药

炸药爆炸是一个极为复杂的物理化学过程。理想炸药爆轰反应速度很快，可不考虑化学反应过程，能量在爆轰波阵面到达的时刻瞬时释放。在非线性动力学数值模拟中，多采用JWL状态方程来描述产物的状态

式中：p是压力，V是产物相对比容，E 是产物的内能，A、B、R1、R2、ω是常数，由圆筒实验拟合得到，PETN的状态方程参数参见文献［10］。

1.2.2 岩 石

炸药爆炸后对岩石加载，初始冲击波强度在吉帕以上，岩石介质在冲击波的作用下粉碎破坏。蓝田花岗岩密度为2 600kg／m3，用分段冲击状态方程描述花岗岩在不同加载条件下的冲击压缩特性［12］

式中：c是应力波波速，ur是粒子速度，单位为m／s。在数值模拟计算时，需假设式（2）可外推，即在粒子速度大于350m／s时和小于10m／s时同样成立。用Von Mises模型描述蓝田花岗岩的强度［12］。

2 计算结果分析

图3是部分计算点的速度曲线。当应力波阵面到达时，粒子开始扰动，距离爆心较近的粒子速度几乎从零直接跃升至最大值，应力波近似冲击波。随着距离r的增加，应力波在几何扩散和物理衰减的作用下，应力波峰值不断降低，导致粒子速度峰值的降低。粒子速度峰值的衰减速度随着距离的增加而逐渐减小，这是因为在爆炸近区，冲击波的强烈压缩作用使得介质粉碎破坏产生不可恢复的塑性变形，消耗掉应力波的大部分能量，而在离爆心较远的区域，应力波的衰减主要由几何扩散效应导致。同时随着距离的增加，粒子速度上升到最大值所消耗的时间逐渐增大。当粒子速度达到最大值后，由于后续稀疏波的追赶卸载，使得粒子速度从峰值逐渐降低到零，随后粒子反向运动达到速度峰值后又逐渐衰减至零，来回扰动几次后，粒子速度逐渐趋近于零。

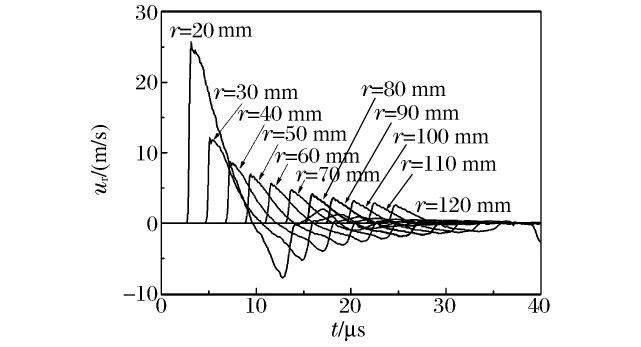
图3 粒子速度时程曲线Fig.3 The time history of particle velocity

图4 粒子位移时程曲线Fig.4 The time history of particle displacement

图4是部分计算点的位移曲线。可以看出随着距离的增加，粒子位移上升到最大值后逐渐回落，并在平衡位置经历一段扰动后最终趋近于平衡位置，即粒子位移的最大值并不是位移的最终平衡值。因为位移是速度对时间的积分，而速度的反向使粒子从最大位移处反向运动。随着距离的增加，粒子的最大位移和平衡位移逐渐减小，由于介质的塑性变形，粒子平衡时的位移不为0。粒子的速度和位移变化趋势与实验结果［10］基本一致，说明数值模拟可用于粒子速度和位移的定性分析。

粒子的运动特性包含了粒子速度和位移峰值，上升时间，脉冲持续时间等。由于实验数据有限，很难对比所有的运动特性，以王占江等［10］的实验结果依据，对比粒子速度峰值和位移峰值，如表1所示。表中W 为等效TNT质量；r为测点的位置；r／W1／3为比例距离。通过粒子速度峰值ur，max和位移峰值Dmax的实验拟合与数值模拟的对比发现，虽然粒子速度峰值和位移峰值随距离的变化区域一致，但是粒子速度峰值的数值模拟和实验拟合结果之间偏差很大，而粒子位移峰值的偏差在20%以内，吻合较好。虽然模拟结果与实验值相差很大，使定量的数值模拟难度很大，但利用数值模拟对运动参数的影响因素进行定性分析是可行的。

表1 粒子运动参数的数值模拟与实验对比Table 1 Comparison of particle movement parameters between simulation and experiment results

3 炸药性质对粒子运动参数的影响

3.1 炸药种类的影响

爆炸释放的能量以应力波的形式传递给岩石介质，引起介质的变形和粒子扰动，所以炸药的爆热对于应力波的影响非常大。除了爆热外，不同炸药具有不同的爆压、爆速以及产物膨胀特性（JWL状态方程）。很难找出爆速、JWL状态方程参数相同而爆压不同的炸药，所以要单独研究这些特性的影响是不现实的。取TNT、PETN和HMX等3种常用理想炸药作为研究对象，主要性能参数和状态方程参数参见AUTODYN材料库，各炸药的质量均为0.125gTNT当量质量，以保证炸药释放的总能量相同。

图5为不同种类炸药对20mm处粒子速度的影响的比较。在爆炸能量相等的条件下，炸药种类对粒子速度的影响较小，图中粒子速度的变化趋势相同。粒子速度峰值的大小关系为：u（HMX）r＞u（PETN）r＞u（TNT）r，与炸药爆压的大小关系一致，但仅存在细微差别。图6为炸药种类对20mm处粒子位移的影响。粒子速度的变化受到炸药种类的影响较大，这是因为速度曲线经过时间积分，细微差别被放大。值得注意的是位移峰值的大小关系为：D（TNT）＞D（HMX）＞D（PETN），与速度峰值大小关系不一致。虽然TNT引起的速度峰值最小，但是粒子速度的衰减要慢于HMX和PETN，说明除了爆压外，其它因素如爆轰产物的膨胀特性也可能会对粒子位移产生影响，但是具体是何种因素起主要作用，还需进一步的研究。

图5 不同种类炸药对粒子速度的影响Fig.5 Particle velocity－time curves influenced by different explosive types

图6 不同种类炸药对粒子位移的影响Fig.6 Particle displacement－time curves influenced by different explosive types

3.2 能量释放速率的影响

非理想炸药中的非理想成分如铝粉在产物膨胀区内缓慢反应（相对于理想成分）释放能量，AUTODYN中用改进的JWL方程描述产物的状态

用P.J.Miller［13］反应速率方程定义非理想成分的反应速率

式中：Q为非理想成分含有的热量，λ为非理想成分的反应度，0≤λ≤1；G、a和b是与反应速率相关的常数，由实验标定。以非理想炸药PW20（ω（RDX）＝80%，ω（Al）＝20%）作为爆炸源，研究非理想成分的反应速率对粒子运动参数的影响。状态方程和反应速率方程参数：ρ0＝1 700kg／m3，A＝927.6 GPa，B＝29.3GPa，R1＝6.5，R2＝1.85，ω＝0.5，E0＝4.88MJ／kg，Q0＝2.27MJ／kg，a＝1／2，b＝1／6。G与炸药特性、铝粉的颗粒形状和尺寸等有关，可通过调整G改变反应速率，G越大，反应速率越快。

图7 不同反应速率对粒子速度的影响Fig.7 Particle velocity－time curves influenced by different reaction rates

图8 不同反应速率对粒子位移的影响Fig.8 Particle displacement－time curves influenced by different reaction rates

图7为反应速率对20mm处粒子速度的影响。虽然释放的总的能量相同，而且炸药的其他性能参数均不变，但是非理想成分能量释放的快慢会影响能量向岩石介质的传递，即能量释放速率影响岩石介质中传播的应力波强度。能量释放速率越快，转化成应力波的能量越多，从介质中的粒子运动角度来说，则粒子速度峰值越高，且粒子正向速度持续时间越长，粒子的位移峰值越大，如图8所示。

4 结 论

利用有限元软件AUTODYN对岩石中爆炸作用下的粒子运动进行数值模拟，得到如下结论：

（1）通过与实验结果对比发现，数值模拟可以较准确地预测粒子的速度和位移变化趋势，但是在定量分析时，所有的运动参量很难同时与实验结果吻合。粒子位移由粒子速度曲线积分得到，所以粒子的位移不仅受到粒子速度峰值的影响，同时与粒子速度的上升时间，脉冲持续时间以及速度的衰减有关。在多种因素的综合影响下，虽然粒子速度峰值与实验结果偏差很大，但粒子位移峰值与实验值的偏差较小，在20%以内。

（2）在爆炸能量相同的条件下，炸药种类对粒子速度峰值的影响较小，而对粒子位移有明显的影响，但很难具体分析某一个因素单方面的影响。所以在对炸药处理时，不能仅仅考虑爆热，而要综合考虑炸药的其他性质，需要进一步的研究。

（3）非理想能量释放速率对粒子的运动有很大的影响。在其他所有性能参数都相同的条件下，反应速率越快，以应力波的形式传递给岩石介质的能量就越大，从而粒子速度峰值和位移峰值越大。由于岩石介质中的爆炸能量可分为应力波能和爆轰产物能，应力波能量的增加意味着爆轰产物的能量减小，能量释放的快慢可以调节2部分能量的比例。

［1］吴亮，卢文波，宗琦.岩石中柱状装药爆炸能量分布［J］.岩土力学，2006，27（5）：735－739.WU Liang，LU Wen－bo，ZONG Qi.Distribution of explosive energy consumed by column charge in rock［J］.Rock and Soil Mechanics，2006，27（5）：735－739.

［2］王耀辉，陈莉雯，沈峰.岩爆破坏过程能量释放的数值模拟［J］.岩土力学，2008（3）：790－794.WANG Yao－hui，CHEN Li－wen，SHEN Feng.Numerical modeling of energy release in rock burst［J］.Rock and Soil Mechanics，2008，29（3）：790－794.

［3］劳俊，肖卫国，王肖钧，等.地下空腔解耦爆炸的数值模拟［J］.爆炸与冲击，2009（5）：535－541.LAO Jun，XIAO Wei－guo，WANG Xiao－jun，et al.Numerical simulation on underground cavity－decoupling explosion［J］.Explosion and Shock Waves，2009，29（5）：535－541.

［4］田振农，张乐文，李世海.岩体中爆腔内压力脉动特征和爆炸能量分布的数值模拟［J］.岩土工程学报，2010（8）：1247－1252.TIAN Zhen－nong，ZHANG Le－wen，LI Shi－hai.Numerical simulation of pulsation features of pressure in explosion cavity and distribution of explosive energy in rock blasting［J］.Chinese Journal of Geotechnical Engineering，2010（8）：1247－1252.

［5］武海军，杨军，黄风雷，等.不同耦合装药下岩石的应力波传播特性［J］.矿业研究与开发，2002（1）：44－46.WU Hai－jun，YANG Jun，HUANG Feng－lei，et al.Propagation behavior of stress wave of rock under the conditions of different coupling charges［J］.Mining Research and Development，2002（1）：44－46.

［6］李清，王汉军，杨仁树.多孔台阶爆破破裂过程的模型试验研究［J］.煤炭学报，2005，30（5）：576－579.LI Qing，WANG Han－jun，YANG Ren－shu.Experimental investigation on fracture process of multi－hole bench blasting［J］.Journal of China Coal Society，2005，30（5）：576－579.

［7］Gran J K，Ehrgott J Q，Cargile J D.Cavity expansion with spherical explosive charges in concrete［R］.US Army Engineering Research and Development Center（ERDC），ERDC／GSL SR－09－4，2009.

［8］王占江，李孝兰，戈琳，等.花岗岩中化爆的自由场应力波传播规律分析［J］.岩石力学与工程学报，2003，22（11）：1827－1831.WANG Zhan－jiang，LI Xiao－lan，GE Lin，et al.Free－field stress wave propagation induced by underground chemical explosion in granite［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（11）：1827－1831.

［9］王占江，李孝兰，张若棋，等.固体介质中球形发散波的实验装置［J］.爆炸与冲击，2000，20（2）：103－109.WANG Zhan－jiang，LI Xiao－lan，ZHANG Ruo－qi，et al.An experimental apparatus for spherical wave propagation in solid［J］.Explosion and Shock Waves，2000，20（2）：103－109.

［10］王占江.岩石中填实与空腔解耦爆炸的化爆模拟实验研究［D］.湖南：国防科学技术大学，2003.

［11］Century Dynamics Incorporated.Interactive non－linear dynamic analysis software user manual［M］.Ramon，USA：Century Dynamics Incorporated，2001.

［12］王占江，张德志，张向荣，等.蓝田花岗岩冲击压缩特性的实验研究［J］.岩石力学与工程学报，2003，22（5）：797－802.WANG Zhan－jiang，ZHANG De－zhi，ZHANG Xiang－rong，et al.Testing study on shock compression for Lantian granite［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（5）：797－802.

［13］Miller P J.A reactive flow model with coupled reaction kinetics for detonation and combustion of non－ideal explosives［C］∥MRS Proceeding.1996，418：413.