水下爆炸冲击作用下重力坝的损伤发展及破坏模式＊

张启灵，李端有，李 波

（1.长江科学院，湖北 武汉 430010；2.水利部水工程安全与病害防治工程技术研究中心，湖北 武汉430010）

大坝作为重要基础建设设施，安全意义重大。各类爆炸对大坝的冲击作用可能引起结构的损伤甚至破坏，直接威胁大坝安全。例如，1937年西班牙Ordunte大坝检修廊道内15t炸药爆炸，大坝受到损伤［1］；1941年Dnjeprostroj大坝廊道内90t炸药爆炸，大坝被炸出缺口［1］；克罗地亚Peruca大坝也遭到了类似破坏［2］。除战争因素外，近年来频发的各类恐怖活动同样对大坝安全构成潜在威胁［3－4］。有证据表明恐怖分子已将某些水坝列入伺机打击的目标，美国政府已正式立法防范水坝人为破坏［5－6］。

近年来有关大坝在爆炸冲击荷载作用下结构的动力响应成为研究热点。李本平等［7］用动力有限元程序LS－DYNA对三峡三期碾压混凝土横向围堰爆破拆除进行了数值模拟，重点分析了上游库水和廊道对爆破拆除效果的影响。李鸿波等［8］用三维动力损伤有限元模型分析了混凝土重力坝及其岩石基础在大坝背水坡面中部被导弹（或炸弹）击中情况下的各向异性脆性动力损伤问题。刘军等［9］用动力有限元程序LS－DYNA研究了两河口土石坝在坝顶接触爆炸作用下的破坏与损伤演化规律。李本平等［10］利用任意Lagrange－Euler计算方法模拟了2枚制导炸弹连续水平打击重力坝下游垂直段中心的侵彻爆炸全过程，重点研究了大坝破坏效应。王山山等［11］将爆炸视为典型的冲击荷载，采用模型实验的方法研究了重力坝顶部在冲击荷载作用下结构的破坏过程。以上研究均是考虑陆上爆炸冲击荷载作用多发生于战时。与陆上爆炸相比，水下爆炸具有隐蔽性强、实施简便的特点，容易被恐怖分子利用。孟会林等［12］采用LS－DYNA数值模拟分析了典型重力坝断面在上游近坝面水中爆炸和上游深水库底坝踵处爆炸冲击荷载作用下的动力响应特性。徐俊祥等［13］在考虑炸药的爆炸、爆炸波的水中传播、水介质与坝体结构的相互作用的基础上对混凝土重力坝的加速度响应以及位移的时程变化进行模拟。文献［12－13］中均采用了有限元程序LS－DYNA，混凝土采用HJC材料模型，基于ALE算法用状态方程描述流体和炸药，通过欧拉单元计算冲击波的传播过程，重点分析了水下爆炸冲击作用下重力坝结构的动力特性和响应。本文中拟采用基于有限元程序ABAQUS／Explicit和声学介质描述流体，爆炸冲击波在声学单元中传播，选取损伤塑性模型描绘混凝土材料的力学性能，同时考虑混凝土的受拉和受压，重点研究水下爆炸冲击作用下重力坝结构的损伤发展规律和潜在破坏模式，为重力坝的反恐防护提供参考。

1 数值模拟原理

有关水下爆炸作用下各类结构响应的数值模拟研究成果众多［14］，已有成果表明应用ABAQUS／Explicit程序模拟各类结构在水下爆炸冲击作用下的动力响应过程是可行的［15－16］，ABAQUS／Explicit程序中的损伤塑性模型（Concrete damaged plasticity）也被证实能够较好预测爆炸荷载作用下钢筋混凝土结构的动态响应和各类破坏模式［17］。

ABAQUS／Explicit程序采用声学介质描述流体，爆炸冲击波在声学单元中传播，在声学介质边界由边界阻抗指定声压和边界法向运动的关系，声学介质表面任意点的阻抗边界条件统一基本方程

该模型中边界阻抗可以被看作是声学介质和某边界之间布置的一系列并联弹簧和阻尼器。式（1）中：p表示声压，p表示声压随时间的变化率，k和c分别表示弹簧的弹性系数和阻尼器的阻尼系数，u是指声学介质（流体）与边界之间的外法向相对速度。边界阻抗是通过阻止声能量在边界面上的反射来实现透射边界条件。特殊地，对于自由面，式（1）中k＝ρg，ρ为流体的密度，g为重力加速度，c趋于无穷大。若流体边界未定义边界阻抗，边界运动加速度始终为0，此时相当于不透射（固定）边界。

在流固交界面上，式（1）中u是指声学介质（流体）与结构体之间的外法向相对速度

式中：uf为声学介质边界面上的速度矢量，um为相应位置结构体的速度矢量，n为声学介质边界面的外法向向量。

ABAQUS／Explicit程序中水下爆炸冲击波对水下结构的冲击荷载与爆炸源位置、冲击波在水中的传播特性和参考点处的冲击波压力时程有关，如图1所示。

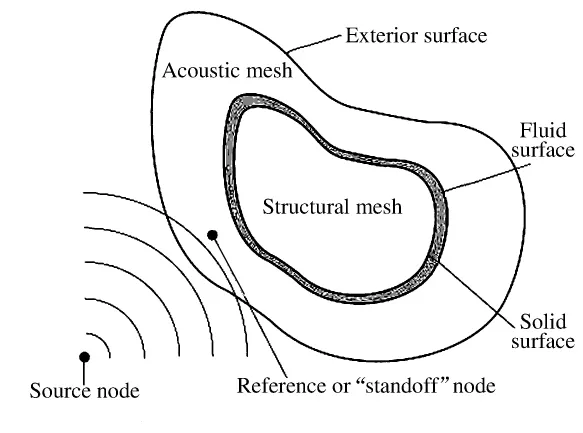
图1 水下爆炸荷载示意图Fig.1 Underwater explosion loading model

参考点位置的选取和该处冲击波压力时程的定义对流固耦合瞬态动力分析至关重要。ABAQUS／Explicit程序要求参考点需定义为冲击波反射面上距爆炸源最近的点，以此保证流固接触面上所有点受到冲击波荷载的起始时刻滞后于参考点。为节约计算时间，参考点位置直接定义在反射面上，这样在时程分析起始时刻冲击波即发生反射，结构开始受到冲击作用。参考点的冲击波压力时程波形可以根据已有实验数据确定，冲击力峰值与装药量以及离爆心距离的关系根据库尔经验公式确定

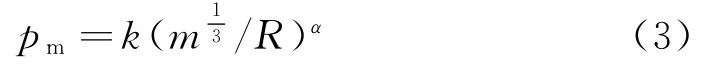
式中：pm为冲击波压力峰值，m为装药量，R为离爆心距离，k和α为与炸药类型有关的经验系数，以下计算的炸药类型假设为TNT，取k＝52.27MPa，取α＝1.13。

参考点的冲击波压力时程确定后，流固接触面上其他点压力时程可以根据冲击波类型和该点与参考点的相对位置确定。假定冲击波自爆炸点向四周球形传播，对于球面波，Abaqus程序默认空间上某点冲击波压力大小与该点和爆炸源的距离有关

式中：pL为该点的冲击波压力，pS为参考点的冲击波压力，R0为爆炸源与参考点的距离，Rj为爆炸源与该点的距离。由于参考点为流固接触面上距爆炸源最近的点，即R0＜Rj，因此pL＜pS。式（4）反映的仅是pL和pS的空间关系，在时域上pL滞后于pS，滞后时间为为冲击波在流体介质中的传播速度。

2 计算条件

以某典型的重力坝坝段结构为研究对象，坝高85m，坝顶宽15m，坝段长20m，上游坝坡1∶0.05，下游坝坡1∶0.65，底部宽为61.5m，下游起坡点距离坝顶20m，上游水深75m，下游无水。文献［13］中的研究表明，水中冲击波引起的坝体动力响应以水平方向为主，且爆炸引起的基础震动对于结构的影响远小于爆炸冲击波的直接作用，而本文中研究重点为坝体混凝土结构，故考虑到计算规模，数值计算模型未包含坝基。水库水体自坝踵向上游延伸3倍坝高（255m）。坝体采用八节点六面体等参单元（C3D8）模拟，水体采用四节点四面体声学单元（AC3D4）模拟，大坝迎水面和水体采用ABAQUS／Explicit程序中的TIE命令实现流固耦合。整个模型含89 450个单元，68 442个节点，其中坝体含55 800个单元，61 341个节点。有限元模型见图2。

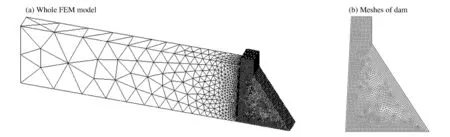
图2 有限元模型Fig.2 Finite element model

坝体混凝土容重25kN／m3，弹性模量28GPa，泊松比0.167，标准抗拉强度1.75MPa，标准抗压强度17MPa，混凝土拉伸和压缩损伤值与应变关系由Mazars模型确定［18］，混凝土损伤后残余应力与应变关系根据文献［19］确定。水体容重10kN／m3，体积模量2GPa，声音在水中的传播速度为1.5km／s。

计算模型采用笛卡尔直角坐标系，其x轴为水平方向，指向下游为正；y轴为铅垂方向，向上为正；z轴为水平方向，指向右岸为正；坐标值单位为m。坐标系原点为坝踵最左端。大坝底部施加全约束，两侧和下游面自由。水体底面按不透射边界处理，两侧和上游面定义为透射边界模拟半无限水域，水面定义为自由面。

参考点的爆炸冲击力时程波形选取Y.W.Kwon等［20］的实验成果，该冲击力峰值15.72MPa，记录持续时间为2ms，时程曲线如图3所示。爆炸源位于坝段长度方向中断面上（z＝10m）。计算分析时长定为0.1s，结果输出步长1ms。

3 坝体损伤发展

3.1 不同水深爆炸作用

为分析炸药在不同水深处起爆时大坝结构的损伤分布和发展规律，假定爆炸源与大坝迎水面水平距离10m，分别考虑爆炸源位于库底（y＝2m）、中部（y＝40m）、下游起坡点高程（y＝65m）和近水面（y＝73m）等情况，记为方案A～D。TNT装药量为50kg，根据库尔经验公式计算得到参考点冲击波压力峰值为16.91MPa。各方案坝体中断面损伤区面积占断面总面积比例随时间的变化如图4所示。

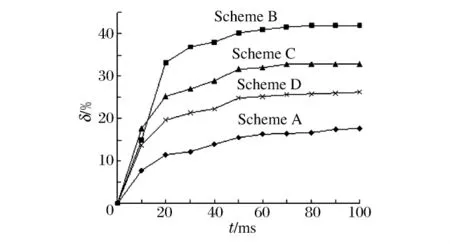
图4 坝体中断面损伤区比例Fig.4 Damage area proportion of dam’s middle crosssection

从图4中可以看出，断面损伤区面积百分比δ在0～20ms内急剧发展；20～60ms损伤区继续发展，但扩散速度减慢；60ms后损伤区范围趋于稳定。这说明在水下爆炸冲击作用下，大坝的损伤发展是一个瞬态过程。从最终的损伤范围看，δB（41.95%）＞δC（32.81%）＞δD（26.26%）＞δA（17.67%）。

图2中坝体模型单元尺寸划分均匀，因此可以近似采用坝体中断面上所有节点的损伤代数平均值δ定性描述坝体的损伤程度。从断面平均损伤值看，δB（0.236）＞δC（0.193）＞δD（0.149）＞δA（0.080）。

比较结果表明，对于损伤范围和损伤程度，爆炸源靠近大坝高度方向中部对坝体破坏作用最强。

3.2 不同爆源距离爆炸作用

方案B情况下坝体断面损伤范围比较大（超过40%），为探寻爆炸源与大坝距离对坝体损伤的影响，在方案B的基础上，将爆源距离设为15、20、25和30m，记为方案B2～B5。各方案（包括方案B）在坝体中断面损伤区如图5所示，损伤区比例和平均损伤值列于表1。

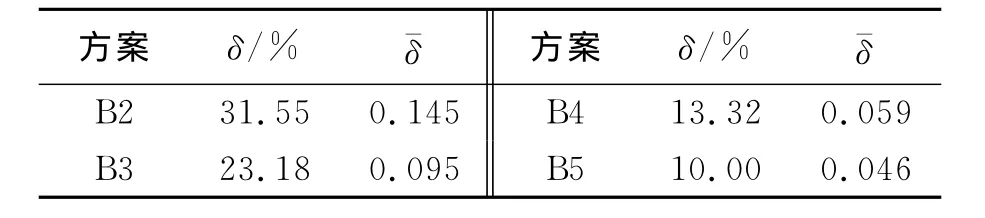
表1 坝体中断面损伤区比例和平均损伤值Table 1 Damage area proportion and average damage variable of dam’s middle crosssection

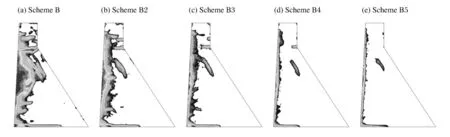
图5 不同爆源距离坝体中断面损伤区Fig.5 Damage area of dam’s middle crosssection with different explosion site distances

从图5和表1可以看出，随着爆源距离的增大，相同装药量爆炸对大坝的损伤作用显著减小。爆源距离较大时（方案B4、B5），损伤区主要集中在上游坝面和坝底上游侧，损伤深度为2～3m；由于应力波向下游传播过程遇到下游坝坡面发生反射，坝体内形成拉伸波，与后续应力波共同作用，坝体中上部存在一条长约12m、宽约2m的损伤带，延伸方向大致平行于下游坝坡面。当距离爆源较近时（方案B、B2、B3），上游坝面损伤区深度显著变大，坝底上游侧损伤区向下游有所延伸，深度变化不明显；坝体中上部损伤带向上游坝面发展，与上游坝面损伤区贯通；另外，坝头部分损伤严重，方案B和方案B2坝头出现顺河向贯穿性损伤区。

4 大坝潜在破坏模式

混凝土结构损伤发展到一定程度即会出现宏观裂缝，最终破坏。通过分析坝体结构的损伤发展范围，可以在一定程度上预测大坝的潜在破坏模式。方案A～D情况下坝体中断面损伤区如图6所示。

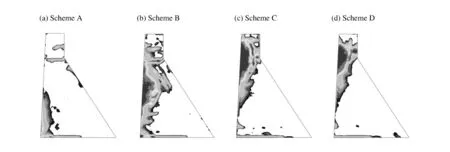
图6 不同水深爆炸作用下坝体中断面损伤区Fig.6 Damage area of dam’s middle crosssection with different explosion site depth

无论哪种方案，坝体近爆炸点区域都是损伤严重的部位，局部区域混凝土结构可能失效，与大坝主体结构分离，造成大坝质量减小或局部缺陷，大坝可能整体溃败或局部失稳倒塌，此为大坝的第1种潜在破坏模式。

爆炸冲击力作用于上游坝面，相对于坝踵处有一个冲击力矩作用，爆炸点越靠近水面，则冲击力矩越大，坝底竖向受拉范围越大。可以预见，当冲击力矩大到一定程度时，坝底损伤区可能从坝踵向下游延伸至坝趾处，这意味着坝体与坝基连接十分薄弱，大坝在上游水压力作用下可能向下游滑动甚至倾倒，从而失去挡水功能，此为大坝的第2种潜在破坏模式。

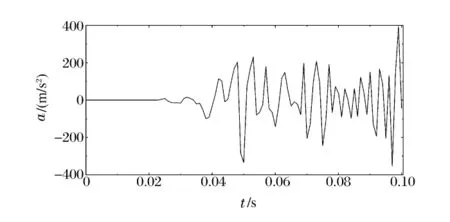
图7 方案A坝顶上游侧中点顺河向加速度时程曲线Fig.7 Acceleration of midpoint on dam crest’s upstream side along stream of scheme A

坝头部分断面尺寸较小，爆炸源靠近坝头（方案C、方案D）时，在冲击力作用下坝头可能破坏。即使爆炸源位于库底（方案A），冲击波通过坝体结构向坝顶传播，引起坝顶顺河向瞬时强烈振动，如图7所示。从图7可以看出，坝顶顺河向振动自25ms后开始明显，0.1s内瞬时顺河向振动加速度峰值接近400m／s2。由于下游起坡点高程上下大坝断面结构发生突变，坝顶顺河向强烈的振动所产生的惯性力导致坝体下游起坡点高程出现局部应力集中，坝头与主体结构连接区域（下游起坡点高程）出现一条水平损伤带，此时坝头可能断裂。以上分析表明，坝头是大坝的薄弱部位，在冲击力作用下坝头可能局部破坏或断裂而倒向下游，造成大坝挡水高度不足，出现漫顶，这也是大坝的第3种潜在破坏模式。

5 结 语

通过一个典型算例，在考虑坝体、库水流固耦合的前提下，分析了水下爆炸冲击作用下重力坝结构的损伤发展规律，预测了3种潜在破坏模式。通过研究发现，从重力坝的反恐防护角度讲，大坝高度方向中部应该成为安防重点；控制爆源距离是有效的手段，以本文中算例为例，当50kg当量TNT炸药的爆源距离控制在30m以上时，水下爆炸冲击对大坝的损坏作用已经不大。除近爆炸点区域外，坝体与坝基连接部位以及坝头部分都是容易损伤的区域，可以考虑增加坝体与坝基连接部位竖向基础插筋，加强坝体与坝基的连接；另外可以考虑局部增加坝头与主体结构连接区域（下游起坡点高程）竖向钢筋，以防坝头局部破坏或断裂而倒向下游，造成灾难性后果。

［1］Jansen R B.Dams and public safety［M］.Denver：US Department of the Interior，Water and Power Resources Service，1980.

［2］Nonveiller E，Rupcic J，Sever Z.War damages and reconstruction of Peruca dam［J］.Journal of Geotechnical and Geoenvironmental Engineering，1999，125（4）：280－288.

［3］Stewart M G，Netherton M D，Rosowsky D V.Terrorism risks and blast damage to built infrastructure［J］.Natural Hazards Review，2006，7（3）：114－122.

［4］Stewart M G.Risk acceptability and cost－effectiveness of protective measures against terrorist threats to built infrastructure considering multiple threat scenarios［J］.Transactions of Tianjin University，2008，14（5）：313－317.

［5］Federal Emergency Management Agency.Dam safety and security in the United States：A progress report on the national dam safety program in fiscal years 2002and 2003［C］∥US Department of Homeland Security，2003.

［6］林祥钦.防恐操作平台：美国对水坝人为破坏的防护策略［J］.大坝与安全，2003（4）：59－61.LIN Xang－qin.Protection dam strategy against terrorism in USA［J］.Dam and Safety，2003（4）：59－61.

［7］李本平，卢文波.廊道和库水对三峡围堰爆破拆除效果影响的数值模拟［J］.爆炸与冲击，2006，26（2）：183－187.LI Ben－ping，LU Wen－bo.Numerical simulation for influence of corridor and reservoir water on blasting－demolition effect of the Three－Gorge cofferdam［J］.Explosion and Shock Waves，2006，26（2）：183－187.

［8］李鸿波，张我华，陈云敏.爆炸冲击荷载作用下重力坝三维各向异性脆性动力损伤有限元分析［J］.岩石力学与工程学报，2006，25（8）：1598－1605.LI Hong－bo，ZHANG Wo－hua，CHEN Yun－min.3Dfinite element analysis of anisotropic brittle dynamic damage in gravity dam under blast－impact load［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（8）：1598－1605.

［9］刘军，刘汉龙，张正珺.爆炸荷载下土石坝动力响应特征的数值模拟［J］.防灾减灾工程学报，2010，30（1）：10－16.LIU Jun，LIU Han－long，ZHANG Zheng－jun.Numerical simulation of dynamic response of an earth and rock－fill dam to a blast loading［J］.Journal of Disaster Prevention and Mitigation Engineering，2010，30（1）：10－16.

［10］李本平.制导炸弹连续打击下混凝土重力坝的破坏效应［J］.爆炸与冲击，2010，30（2）：220－224.LI Ben－ping.Damage effect of a concrete gravity dam under continuous attacks of guided bombs［J］.Explosion and Shock Waves，2010，30（2）：220－224.

［11］王山山，任青文.重力坝在冲击荷载作用下破坏模型试验［J］.水力发电学报，2010，29（5）：11－13.WANG Shan－shan，REN Qing－wen.Experimental study of the gravity dam damage caused by impact load［J］.Journal of Hydroelectric Engineering，2010，29（5）：11－13.

［12］孟会林，刘代志，孙新利.水中爆炸荷载下混凝土重力坝动力特性分析［M］国家安全地球物理丛书：三：地球物理探测与应用：西安：西安地图出版社，2007：212－221.

［13］徐俊祥，刘西拉.水中爆炸冲击下混凝土坝动力响应的全耦合分析［J］.上海交通大学学报，2008，42（6）：1001－1004.XU Jun－xiang，LIU Xi－la.Full coupled simulation of concrete dams subjected to underwater explosion［J］.Journal of Shanghai Jiaotong University，2008，42（6）：1001－1004.

［14］胡春红，冯新，李昕，等.水下爆炸作用下结构响应的数值计算研究综述［J］.工程爆破，2007，13（1）：28－34.HU Chun－hong，FENG Xin，LI Xin，et al.Review of numerical simulation of structural responses to underwater explosion［J］.Engineering Blasting，2007，13（1）：28－34.

［15］Cichocki K.Effects of underwater blast loading on structures with protective elements［J］.International Journal of Impact Engineering，1999，22（6）：609－617.

［16］姚熊亮，张阿漫，许维军，等.基于 ABAQUS软件的舰船水下爆炸研究［J］.哈尔滨工程大学学报，2006，27（1）：37－41.YAO Xiong－liang，ZHANG A－man，XU Wei－jun，et al.Research on warship underwater explosion with ABAQUS software［J］.Journal of Harbin Engineering University，2006，27（1）：37－41.

［17］HUAN Yi，FANG Qin，CHEN Li，et al.Evaluation of blast－resistant performance predicted by damaged plastici－ty model for concrete［J］.Transactions of Tianjin University，2008，14（6）：414－421.

［18］江见鲸，陆新征，叶列平.混凝土结构有限元分析［M］.北京：清华大学出版社，2005.

［19］中华人民共和国建设部.GB 50010－2002混凝土结构设计规范［S］.北京：中国建筑工业出版社，2002.

［20］Kwon Y W，Fox P K.Underwater shock response of a cylinder subjected to a side－on explosion［J］.Computers and Structures，1993，48（4）：637－646.