高速杆条对薄靶板切割毁伤影响因素分析*

张刘成，李向东，刘 刚

(南京理工大学机械工程学院，南京 210094)

0 引言

杆条破片侵彻能力强，长径比大，能够对目标结构件产生切割破坏，是一种有效的终点毁伤元素。目前对杆条破片的侵彻能力已有较多的研究。胡景林等[1]利用经验公式计算了杆状破片对A3钢靶的极限穿透速度并进行了试验验证，靳佳波等[2]利用LS-DYNA对高速杆条小着角侵彻靶板进行了数值模拟，卢永刚等[3]对BRL的THOR方程进行了修正，得到了杆条复杂姿态下的穿甲分析模型，提供了杆条极限穿透速度、剩余速度等的计算方法。但关于杆条破片的切割毁伤特性的研究尚不多见，John G Avery[4]曾提出一个用于预测高速杆状破片对金属结构损伤尺寸的分析模型，但侯日立、涂明武等人[5]指出直接用该模型计算的切口尺寸比实际偏长。文中建立了杆条对薄靶板切口长度的投影方法计算模型，并对典型入射条件下的投影计算结果进行了数值模拟验证。投影计算模型可以为目标易损性研究提供参考。

1 影响杆条切割毁伤特性的因素

当杆条切割薄靶板时，可能直接穿透靶板，也可能出现穿不透、跳飞等情况。杆条切割靶板的结果与杆条、靶板以及入射条件有关。杆条因素包括杆条的材料性能、长径比、截面形状等;靶板因素包括靶板的材料性能、厚度等;入射条件包括杆条的着靶速度(弹目相对速度)v、攻角(速度与杆条之间的夹角)β、入射角(杆条速度与靶板法线之间的夹角)α、面角(杆条和杆条速度所在的面与靶面之间的夹角)γ以及杆条自身的旋转因素等。杆条对薄靶板的切割毁伤特性主要表现在杆条穿过薄靶板时，在靶板上留下的切口长度和宽度，文中杆条具有较大的长径比，切口宽度的变化和切口长度相比不显著，文中重点研究切口长度的变化规律。高速杆条切割薄靶板，作用过程时间很短，约几十微秒，可忽略杆条的自身旋转。综上所述，当杆条和靶板一定时，杆条的切割毁伤特性主要受着靶速度v、攻角β、入射角α及面角γ四个因素的影响，如图1所示。

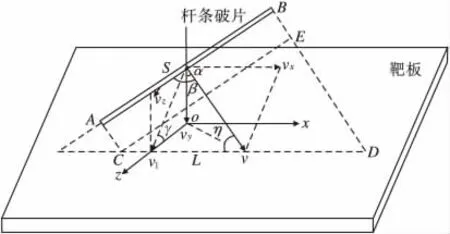
图1 杆条着靶姿态示意图

2 杆条切割毁伤特性的投影计算模型

在杆条切割靶板的模型中建立直角坐标系，y轴穿过杆条的质心，同时垂直于靶板面。当面角γ≠0时，入射面与靶板面相交，其交线为直线CD，交线与速度方向之间的夹角设为η，如图1所示。

虽然杆条长度尺寸S远远大于其端面的尺寸，但当杆条端面与速度方向不平行时，杆条截面尺寸S1对切口长度的影响比较重要，因此需要计算杆条端面尺寸对切口长度的影响，则切口长度分为两部分：一是杆条长度影响部分，设为L1;二是破片端面尺寸影响部分，设为L2。A、B为杆条的两个端点，当不考虑杆条自身的旋转时，杆条将沿着速度v方向飞行，端点A运动到C点时与靶板接触，此时端点B运动到E点，杆条开始侵彻靶板，并在靶板上形成CD长的切口，CD长设为 L，则 L=L1+L2。

由图1分析杆条的速度，在直角坐标系中，杆条速度由沿坐标轴x、y、z三个方向组成，即：

根据三角形正弦定理知：

式中：L1为待求量，β为变量，S是已知量，其中∠BDC= η。因此：

为了求出切口长度L1，则必须先知道η的值。下面在速度三角形中计算η：

1)由杆条速度分析可知，vy=vcosα

3)在入射面中可知，v1=vsinη

由上述可得出：

因此，可以得到杆条长度影响造成的切口长度：

如图2所示，∠a=90°－ α，∠b=90°－ β，S1为杆条A端端面尺寸，根据三角形正弦定理知：

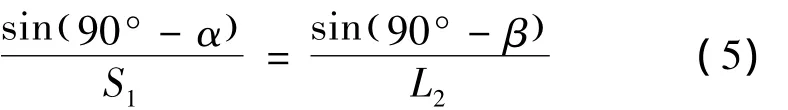
即得出杆条端面尺寸影响造成的切口长度：

由此杆条侵彻靶板的切口长度：

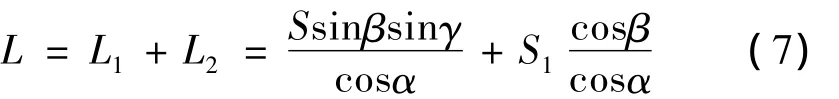
图2 杆条A端放大示意图

3 杆条切割毁伤特性的数值模拟

3.1 有限元模型及材料参数

有限元模型如图3所示，薄靶板厚6mm，长200mm，宽100mm，边界采用固定约束;圆截面杆条直径4.25mm，长100mm。杆条和靶板均采用单点积分Lagrange六面体单元划分网格，使用面面侵蚀接触算法。

图3 杆条切割靶板有限元模型

计算时，杆条和靶板均采用JOHNSON_COOK材料模型和GRUNEISEN状态方程。其屈服应力表达式为：

式中：A、B、C、n及m为与材料相关的常数;εp为有效塑性应变为有效塑性变应率;T*=(TTroom)/(Tmelt－Troom)为无量纲温度，其中Tmelt与Troom分别表示材料的熔点与室温。

断裂处的应变为：

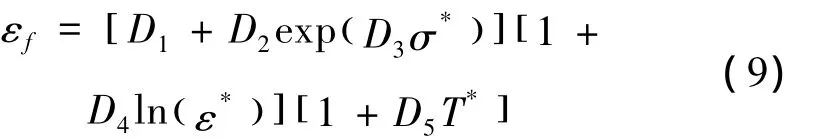
杆条采用20#钢，靶板采用Q235钢，主要材料参数见表1。

表1 杆条和靶板的主要材料参数

3.2 杆条切割靶板过程

由对杆条切割毁伤特性的影响因素分析可知，杆条切割靶板结果除了受杆条和靶板自身因素的影响，还受到杆条入射条件的影响。图4和图5分别描述了两种典型入射条件下，杆条穿透靶板和出现跳飞两种状态。图6为两种过程中杆条的速度变化曲线。

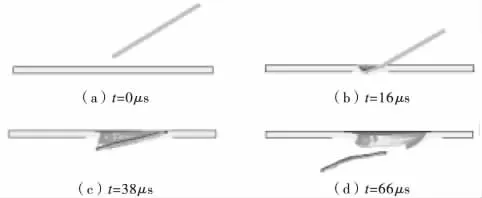
图 4 杆条穿透靶板(v=1900m/s、α =30°、β =30°、γ =90°)

图 5 杆条跳飞(v=1900m/s、α =60°、β =45°、γ =90°)

3.3 数值模拟结果分析

3.3.1 杆条速度对切割毁伤特性的影响

固定入射面和靶面之间的夹角γ=90°、入射角α=30°、攻角β=90°，模拟在不同速度下杆条对薄靶板的侵彻，结果如图4所示。由图可知，当杆条速度为1800m/s时，靶板上有较深的撞痕，且有少许穿透，随着杆条速度的增加，穿透部分增大，直到撞痕面全部穿透。在不同杆条速度下，撞痕长度基本相同，即杆条速度不影响切口长度。为了让杆条尽可能穿透，以下计算取杆条速度为2000m/s。

图6 杆条速度随时间变化曲线

图7 杆条在不同速度下对靶板的侵彻

3.3.2 攻角及入射角对切割毁伤特性的影响

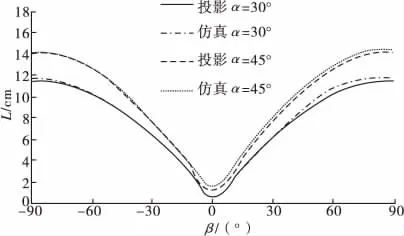
图8 攻角及入射角对切口长度的影响

杆条对薄靶板的切割毁伤效果随着攻角、入射角及面角的变化而变化，着靶姿态影响着杆条对靶板的切割毁伤效果。杆条着靶姿态很多，这里选取面角γ =90°，入射角α =30°和α =45°两种典型情况，模拟不同攻角β条件下，杆条对靶板的侵彻，并将结果与投影计算结果进行对比，如图8所示。由曲线可以看出，投影计算结果与模拟计算结果变化规律非常一致，切口长度随攻角绝对值的增大而增大，随入射角的增大而增大。只是投影计算结果略小于数值模拟计算结果，且当攻角β在零点附近时，切口长度较小，两种方法所得结果差值较大;当攻角大于15°时，两种方法所得结果差值较小，在10%以内。

3.3.3 面角对切割毁伤特性的影响

在杆条切割靶板的过程中，面角γ起着重要的作用，为了研究γ对切口长度的影响，选取α=30°、β=90°的典型情况，模拟γ在60°～90°之间变化时杆条对靶板的侵彻，得到切口长度随面角γ的变化曲线，同时列出对应的投影计算结果，如图9所示。由图可知，两条曲线变化规律相同，切口长度随面角的增大而增大，投影计算所得曲线略低于模拟计算所得曲线，但两者差值很小，随着γ的变化，两者差值一直在10%以内。

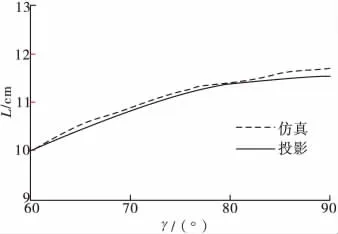
图9 面角对切口长度的影响

4 结论

文中对影响杆条切割毁伤特性的因素进行了分析，指出杆条对薄靶板的切割毁伤特性除了受杆条和靶板自身因素影响外，还受到杆条速度、攻角、入射角及面角等入射条件的影响;然后建立了高速杆条对薄靶板切口长度的投影计算模型，并对典型入射条件下杆条对薄靶板的切割毁伤进行了数值模拟，模拟计算结果与投影计算结果规律一致，杆条长度随攻角、入射角、面角的增加而增大，攻角大于15°时，投影计算结果与模拟计算结果差值在10%以内。当杆条能够穿透靶板时，用投影计算模型预测高速杆条对薄靶板的切口长度具有较好的精确度，该投影计算模型可用于目标易损性分析。

[1]胡景林，张运法.杆状破片对A3钢板的极限穿透速度研究[J].弹道学报，2001，13(2)：18－22.

[2]靳佳波，王树山，司红利.高速杆条小着靶角侵彻靶板的三维数值模拟[J].弹箭与制导学报，2003，23(1)：160－161.

[3]卢永刚，杨世全.基于THOR方程的杆条复杂姿态穿甲分析模型[J].弹箭与制导学报，2005，25(1)：27－30.

[4]John G Avery.Design Manual for lmpact damage tolerant aircraft structure，AD－ A 109290[R].1982.

[5]侯日立，涂明武，孙峰山，等.一种离散杆战斗部威胁下的飞机损伤计算模型[J].计算机仿真，2006，23(6)：85－87.