组合导航中抑制自适应滤波发散的研究*

宋 杰，晋 帆

(昆明理工大学信息工程与自动化学院，昆明 650500)

0 引言

现代主要的导航系统有捷联惯导系统(SINS)、卫星全球定位系统(GPS)、无线电导航和组合导航系统等。其中SINS有误差积累的问题，而GPS的信号容易受到遮蔽和干扰。对于高速运动和长时间飞行的载体，用单一的导航系统，很难达到理想的导航精度。为了提高导航的精度，采用将几种导航系统组合起来，能有效提高导航的精度，更好的满足载体对导航系统的要求[1－2]。

在组合导航系统中，如何将数据进行有效的融合成为一个关键问题。常用的方法是卡尔曼滤波(Kalman filter，KF)，卡尔曼滤波是一种最小方差估计的方法。比较常用的还有Sage-Husa自适应卡尔曼滤波，利用观测数据进行滤波递推的同时，通过时变噪声估值器，实时估计和修正系统噪声和量测噪声的统计特性。Sage-Husa自适应卡尔曼滤波的滤波精度要优于卡尔曼滤波，但是Sage-Husa自适应卡尔曼滤波容易出现滤波发散，其中稳定性和收敛性不能完全保证。文中主要针对Sage-Husa自适应卡尔曼滤波的发散进行研究，采用一种改进的自适应卡尔曼滤波抑制滤波发散，并且通过与卡尔曼滤波器的比较来验证滤波效果。

1 SINS/GPS组合导航原理

捷联惯性导航系统(SINS)的核心是用计算机来实现的惯性平台。SINS用捷联陀螺仪测量的载体角速度解算姿态矩阵，从姿态矩阵的元素中提取载体的姿态和航向信息;并用姿态矩阵把加速度计的输出从载体坐标系变换到导航坐标系，然后进行导航解算[1]。在SINS中，对于高速运行和长时间的飞行后，其积累误差越来越大，使精度降低。在组合导航系统中，需要借助GPS的输出来提高组合导航系统的精度。

在文中，导航坐标系采用东－北－天地理坐标系。在组合导航系统中，其组合方式是采用位置速度组合的方式，用GPS和SINS输出的位置和速度信息的差值作为观测量，经组合的滤波器估计惯性导航系统的误差，然后对惯性导航系统进行校正。SINS/GPS组合导航系统的结构图如图1。

图1 SINS/GPS组合导航系统的结构图

2 抑制滤波发散

2.1 常规卡尔曼滤波

组合导航系统离散数学模型的状态方程和量测方程：

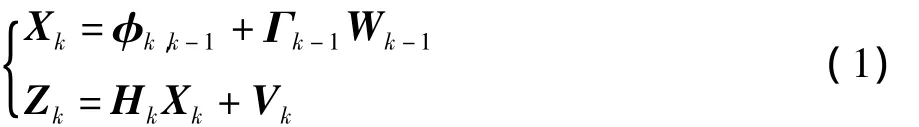
式中：Xk为k时刻的18维状态向量，也是被估计向量;Zk为k时刻的6维量测向量;φk为k－1到 k时刻的系统一步转移矩阵(18×18阶);Wk－1为k－1时刻的系统噪声;Гk－1为系统噪声矩阵;Hk为k时刻的量测矩阵(6×18阶);Vk为k时刻的6维量测噪声。系统噪声是不相关的高斯白噪声。卡尔曼滤波是一种基于误差方差最小准则的递推线性最小方差估计算法，其离散卡尔曼滤波方程如式(2)～式(6)：

其中式(2)和式(5)是时间修正方程，其余3个方程是量测修正方程。式中：Rk和Qk分别称为系统噪声和量测噪声的方差矩阵;Kk为滤波增益矩阵;Pk为估计均方差矩阵，而Pk|k－1为一步预测均方差误差矩阵。

2.2 自适应Sage-Husa滤波算法的改进

自适应Sage-Husa滤波是在卡尔曼滤波算法的基础上改进的一种算法，为了提高估计值的精度。在这种滤波方式中，Sage-Husa自适应卡尔曼滤波算法的滤波流程与卡尔曼滤波的方式是一样的。只是在随着滤波的递推算法中，实时的估计系统噪声和量测噪声[2－3]。其中时变噪声统计递推估值器为：

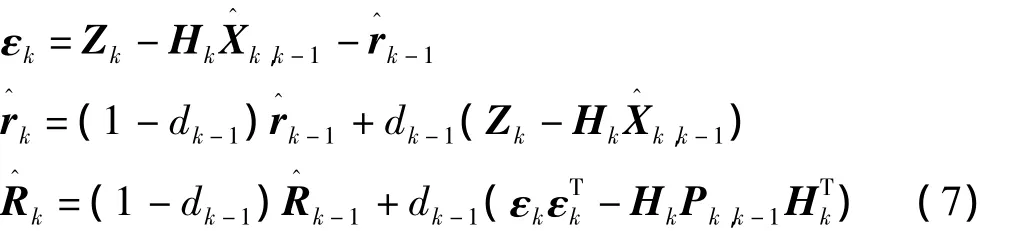
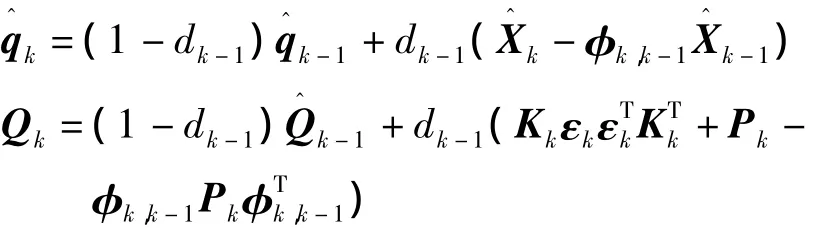
其中，dk－1=(1－b)/(1－bk)，0＜b＜1为遗忘因子。通常取b的范围为0.95＜b＜0.995。在对系统噪声统计特性的计算过程中，由于系统噪声和量测噪声的方差矩阵在递推的过程中，方差矩阵变得越来越大，造成Pk趋向无穷大，使得滤波发散，不能再修正系统噪声和量测噪声。

为了抑制滤波的发散，对自适应Sage-Husa滤波中的Rk和Qk进行改正来解决滤波发散的问题。改进滤波算法后，其时变噪声统计递推估值器变为：

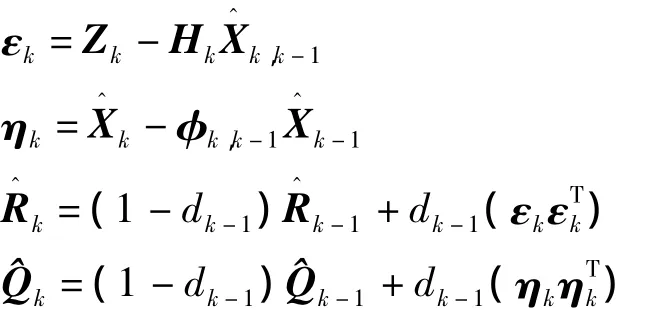
改进后的自适应Sage-Husa算法是实时计算滤波过程中的系统噪声和量测噪声，然后用获得的系统噪声和量测噪声求出当前时刻的系统噪声和量测噪声的方差矩阵，并通过与以前时刻的系统噪声和量测噪声的方差矩阵计算出总体的方差矩阵。这样可以使得方差矩阵Rk和Qk比较稳定，使Pk变得越来越大，起不到修正的作用，造成滤波发散。

3 仿真结果与分析

文中仿真的过程中，惯性导航系统的陀螺随机常数为 0.1°/h，随机漂移均方差为0.1°/h，一阶马尔可夫噪声驱动白噪声均方差为0.1°/h，相关时间为200s;加速计一阶马尔可夫噪声驱动白噪声的方差为0.5m/s，相关时间为100s。GPS接收机随机伪距测量误差为50m，随机伪距测量误差为5m/s。初始位置为北纬30°、东经30°，海拔高度为1000m。飞行航迹在前100s内以90m/s的速度飞行，在后100s内以60m/s的速度飞行。

经过仿真之后得到的结果如图2～图6。

通过仿真结果图可以看出在前20s内，改进后的自适应滤波器在各项导航参数的变化范围比较大;如果采用自适应Sage-Husa滤波器的方法进行滤波，很容易造成滤波的发散。但是改进后的自适应滤波在后续的时间内没有表现出发散现象。比较在经度、纬度和高度的位置误差，可以明显看出，改进后的自适应滤波器的滤波精度要高于卡尔曼滤波器，而且比较稳定。在东、北和天向速度的滤波过程中，在速度变化时刻第100s，可以看出自适应滤波在此时刻，东、北和天向速度都有明显的变化，而在卡尔曼滤波器中则看不到这种变化，符合卡尔曼对方差总体的估计。

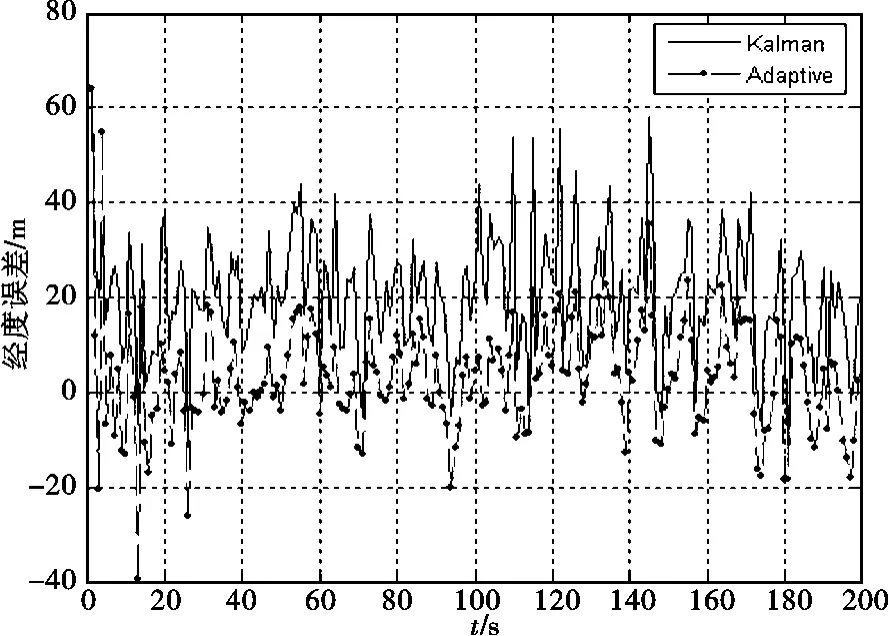
图2 经度误差曲线

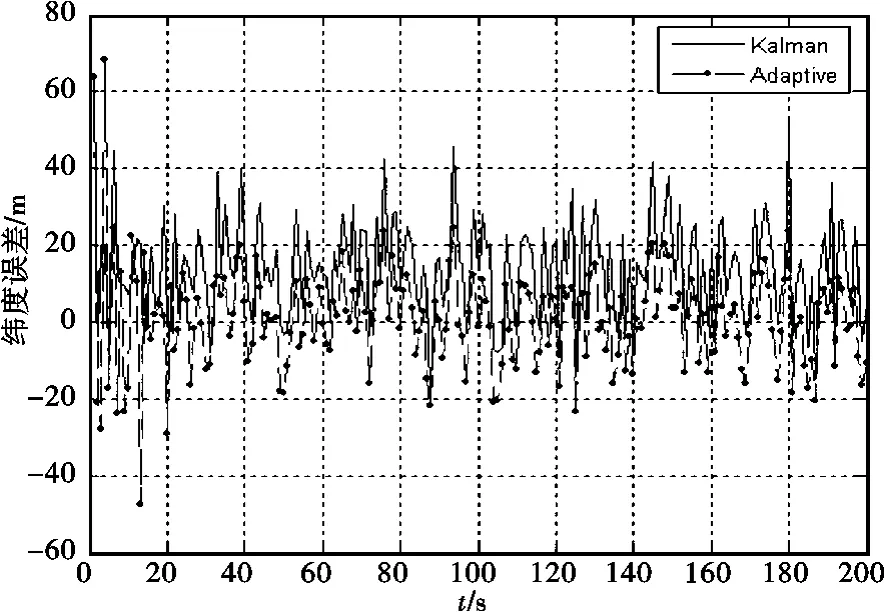
图3 纬度误差曲线

图4 高度误差曲线

图5 东向速度误差曲线

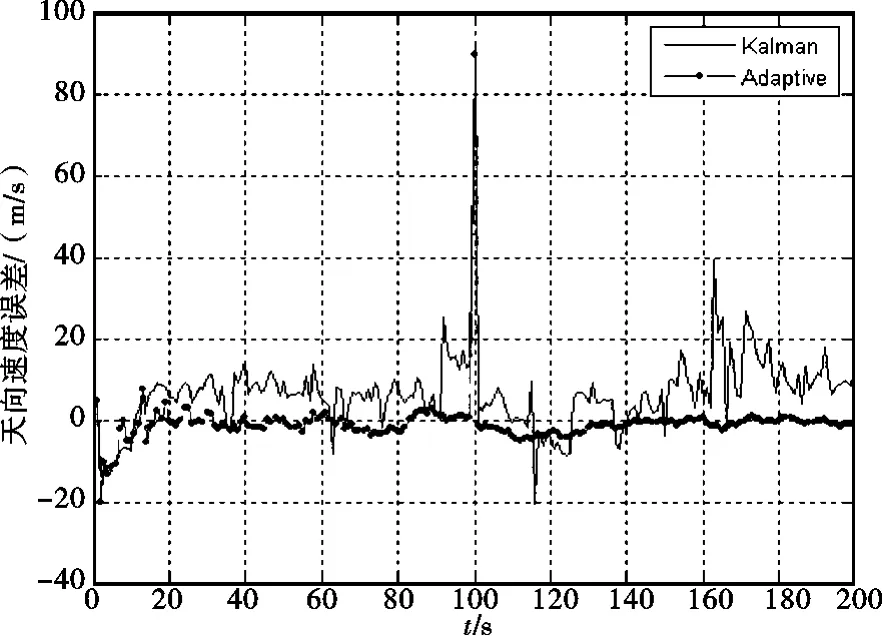
图6 天向速度误差曲线

图7 天向速度误差曲线

4 结论

通过以上的仿真实验结果可以看出，经过改进的自适应Sage-Husa滤波器能够避免滤波的发散，通过与卡尔曼滤波的比较，能够获得较高的精度和比较稳定的状态。但是在状态发生变化时，会引起各项导航参数精度的波动。

[1]刘建业，曾庆华，赵伟，等.导航系统理论与应用[M].西安：西北工业大学出版社，2010.

[2]赵俊梅.GPS/SINS组合导航系统滤波算法研究[D].太原：中北大学，2006.

[3]周媛媛.基于非线性模型的组合导航滤波算法研究[D].上海：上海交通大学，2008.

[4]宋迎春，陈正阳.GPS/INS组合导航中的自适应滤波算法[J].湘潭大学自然科学学报，2006，28(2)：95－98.

[5]周爱军，任光，郭模灿，等.一种新的自适应估计方法在组合导航系统中的应用[J].中国造船，2009，50(1)：69－74.