基于MEMS陀螺仪的轨迹球研究
赵文宏,徐乐俊,宋 闯,王章权,陈程远,周海军
(1.浙江工业大学 机械工程学院,浙江 杭州310014;2.浙江丽水学院计算机与信息工程学院,浙江 丽水323000;3.浙江树人大学 信息科技学院,浙江 杭州310015)
0 引言
众所周知,精密球作为精密仪器中的一个重要元件,在精密工程领域占有一个重要地位。随着许多专家学者提出了很多新的加工工艺和研磨方式,精密球的加工与制作技术近几年取得了飞速发展。浙江工业大学超精密加工研究团队提出一种新型的研磨方式——双自转研磨方式[1],该研磨方式在理论上能够提高研磨均匀性,能够实现对球坯的高效研磨。然而还尚未有检测装置用来检测精密球在研磨过程中的运行轨迹,未能给出研磨轨迹均匀性的定量评价。
MEMS陀螺仪能测得载体的转动角速率,通过公式解算,从而获得载体的姿态信息。本研究基于MEMS陀螺仪的这一特性设计了一种检测装置,通过误差补偿使系统零偏处在合理的范围内。将此检测装置置于研磨球内,在双自转球磨机上做研磨实验,对实验得到的研磨轨迹进行分析,可以得出双自转研磨方式研磨均匀性程度。
1 工作原理
陀螺仪是测量运动物体相对惯性空间绕其输入轴角运动的惯性传感器,可以通过测量得到角速度,对角速度进行积分得到运动载体在一瞬间相对某一基准的角位置信息[2]。运用这一原理,可以由陀螺仪输出角速度,通过积分而得到轨迹球相对于初始定坐标系的3个姿态角:航向角、俯仰角和倾斜角。得到轨迹球的姿态角后就可以完成由载体坐标系到初始定坐标系的转换,如图1所示。
由轨迹球坐标系OX″Y″Z″到初始定坐标系OXYZ的变换可以经过绕Z,Y,X三个坐标轴依次旋转α,β,γ来完成
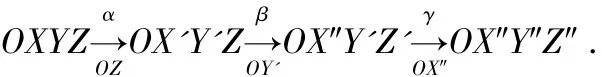
经过三次坐标转换后其变换关系为
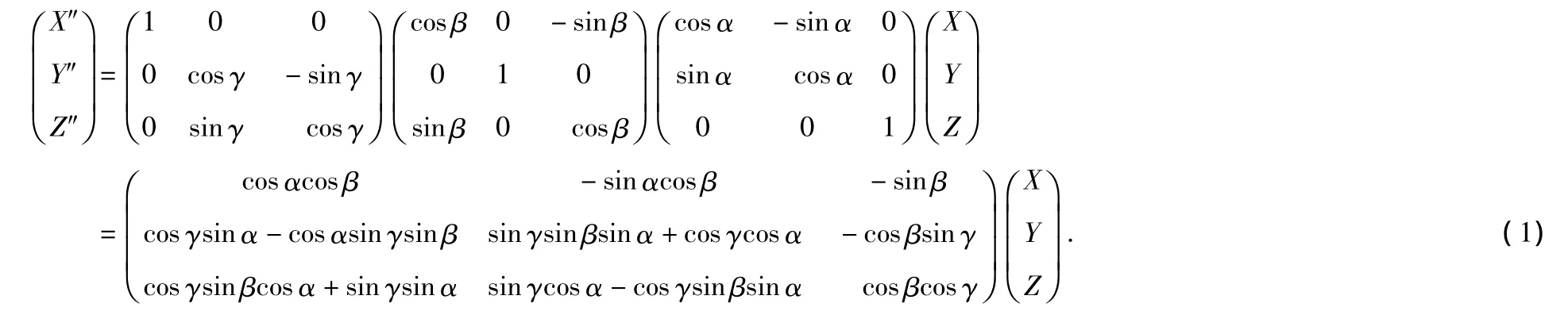
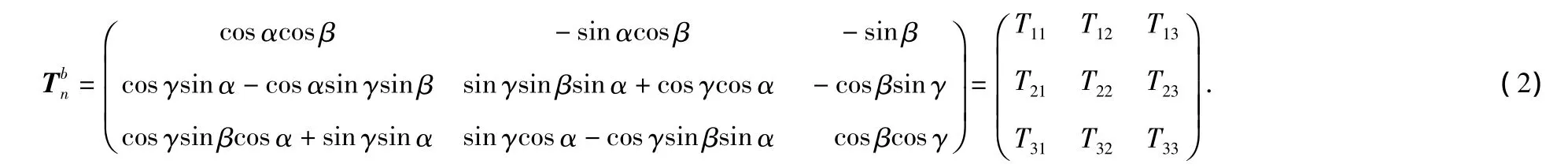
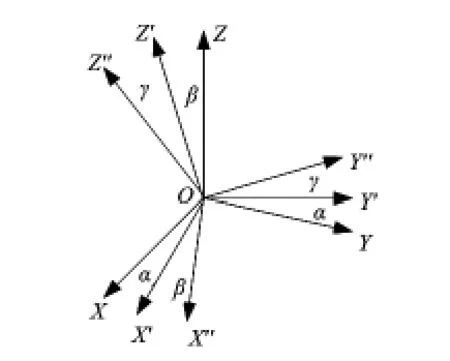
图1 载体坐标系和地理坐标系之间的关系Fig 1 Relation between carrier coordinates and geography coordinates
可以看出:若知道在载体坐标系中的坐标,通过公式(1)解算则可以得到地理坐标系中的坐标值。
在轨迹球上按经纬度将球表面划分为10×10个区域,经度 θ∈(-π,π),纬度 φ∈(-π/2,π/2),统计出研磨实验后落在各个区域轨迹点的个数P。由于随着纬度的不同,球表面各区域面积(A)不同,所以,需要正则化,公式为F=P/A。将各个区域的F做标准差,标准差越小,则说明轨迹球的研磨均匀性越好,标准差越大,则说明轨迹球的研磨均匀性越不好[3]。
2 系统设计
2.1 MEMS陀螺仪的选用
本系统采用的是IvenSense公司生产的ITG3200三轴MEMS陀螺仪(X轴为pitch、Y轴为roll、Z轴为yaw),整合性三轴消除了轴间干扰。内部整合了3个16位A/D转换器,数字输出,无需外部接高分辨率A/D转换器。ITG3200整合了数字低通滤波器,温度传感器,以及快速模式的I2C串行接口(400 kHz),温漂小,噪声低,满刻度范围可达2000°/s,噪音系数为0.03°/s/Hz,交叉轴隔离为±2%,以及高达10,000 gn的耐震度,宽电压供给(2.1~3.6 V)。采用4 mm×4 mm×0.9 mm QFN封装,静态电流只需5μA[4]。
ITG3200的系统框图如图2所示,传感器内部嵌有时钟源,也可通过引脚1外接32.768kHz或19.2 MHz的时钟源。3个方向上的传感器分别获取各轴上的角速度信息,利用ADC将模拟信号转换为数字信号,经过信号处理之后将数据存在寄存器中,然后利用I2C总线与系统通信,引脚9置位高低电平分别代表I2C通信时不同的从器件地址,引脚23为I2C通信的时钟信号引脚,引脚24为I2C通信的数据信号引脚,引脚12为中断引脚。传感器内部还有温度传感器,在ADC转换为数字信号后也可通过I2C与系统通信。
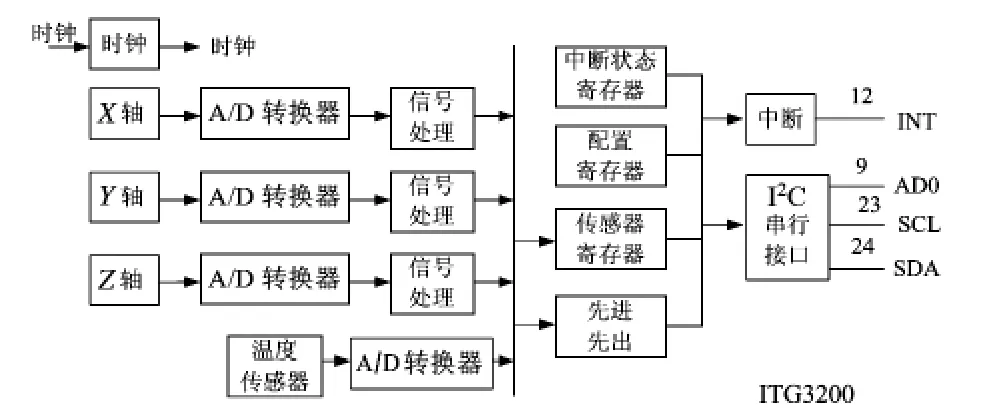
图2 ITG3200框图Fig 2 Block diagram of ITG3200
2.2 系统设计
系统中三轴陀螺仪采集载体(即轨迹球)在三轴方向上的旋转角速度并转换为数字信号,通过I2C总线完成陀螺仪与STM32F103RC微控制器的通信,同时利用SPI总线把角速度信号存储在SD卡中,运用无线模块和PC机通信将数据传输到PC机中,最后在PC机中进行通过公式解算轨迹点坐标,得到轨迹球的运动轨迹。
系统组成如图3所示,主要包括STM32F103RC微控制器、ITG3200三轴陀螺仪模块、SD卡模块、无线模块、电源模块、PC机。在电源模块,由于系统将放入轨迹球内,所以,电源采用钮扣电池供电,而非开关电源等其他供电模式。三轴陀螺仪虽然内部嵌有时钟源,但由于不精准,因此,采用外部32.768 kHz的晶振作为时钟源。MAX3232作为串口调试使用。
在系统软件设计方面,由于采用钮扣电池,所以,必须采取低功耗模式。系统软件设计选择睡眠模式、降低系统与外设时钟等方法来降低功耗,同时设置1ms采集一次数据,采集完之后就关掉SD卡模块等的外设时钟。
3 单轴实验与误差补偿
环境温度的变化对硅微陀螺仪的性能有较大影响,主要表现之一为陀螺仪的零偏随温度变化有较大偏移,本研究采用最小二乘法补偿零偏随温度变化而有的较大偏移[5,6]。实验方法:将ITG3200三轴陀螺仪放入温控箱内,测量的温度范围为10~60℃,每隔5℃测量一次零偏,每次先将陀螺仪放入温控箱30 min,使陀螺仪内部温度和环境温度相同之后再工作,采样频率为1 kHz,采样时间为60 s。将实验得到的陀螺仪输出角速度积分得到角度,60 s之后角度累积误差如图4所示。
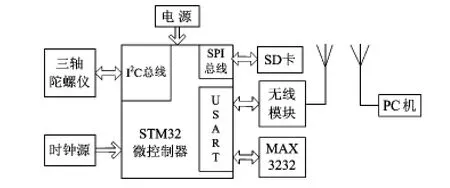
图3 系统框图Fig 3 System block diagram
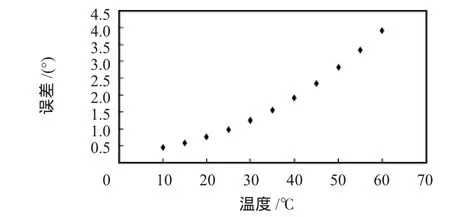
图4 未经补偿的陀螺仪零偏误差Fig 4 Gyro’s zero-offset error without compensation
对于上述温度—零偏累积误差数据,采用最小二乘法进行多项式曲线拟合,曲线拟合函数形式为
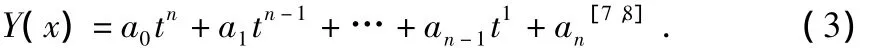
提高多项式的阶次能使拟合程度更高,然而阶次过高使得计算复杂,影响系统的实时性[9]。鉴于此,本文采取三阶多项式模型。经计算可得 a0=0.000 002 12,a1=0.00078,a2=0.00525,a3=0.3184,即
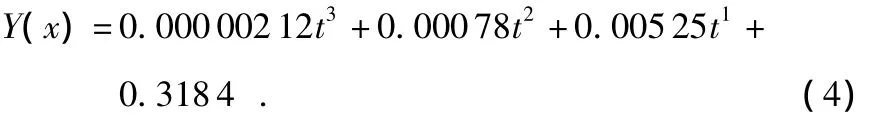
拟合后的曲线如图5所示,由图可见,拟合程度良好。将误差补偿模型对中立点进行温度实时补偿,重复上述实验,得出陀螺仪在各温度下的零偏累积误差都在1°左右,如图6所示。实验结果表明:最小二乘法能显著减小陀螺仪因温度变化而产生的偏移,补偿效果明显,使误差在合理的范围之内,在一定程度上能够满足工程应用。
4 磨球实验
为了得到双自转研磨和传统研磨均匀性的比较,分别将轨迹测量系统进行双自转研磨和传统研磨。双自转研磨方式实验方法:将轨迹测量系统放入轨迹球内,在双自转磨球机上进行实验,实验时间 t=60 s,研磨盘半径 R=300 mm,轨迹球半径 r=50 mm,内研磨盘研磨速度vb=20 r/min,外研磨盘转速 vc=(40sin2πt+20)r/min,上研磨盘转速va=0 r/min。传统研磨方式实验方法:将轨迹测量系统放入轨迹球内,在磨球机上进行传统研磨方式实验,仅使vc=20r/min,其他实验条件不变。实验结束后根据公式(1)计算轨迹坐标值,在轨迹球上划分10×10个区域,统计各区域的个数P,在各区域分别做正则化(F=P/A),根据得到的F做标准差,最后得到双自转研磨和传统研磨的轨迹均匀性如图7所示。由图可见,双自转研磨方式较传统V型槽研磨方式均匀性好。
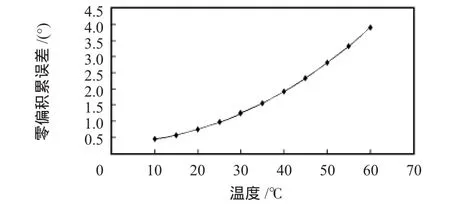
图5 三阶拟合曲线Fig 5 Fitting curve of three orders
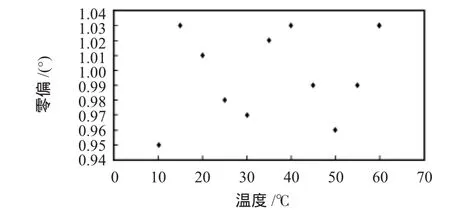
图6 最小二乘法补偿后的零偏累积误差Fig 6 Zero-offset error after compensated by least square method(LSM)
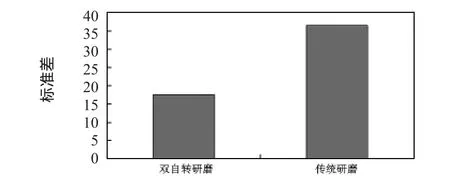
图7 不同研磨方式下研磨轨迹点的标准差Fig 7 Standard deviation of lapping track points with different lapping method
5 结论
本文基于微惯性测量器件测量载体相对惯性空间角速度的原理,将角速度信号积分得到角度,转换到地理坐标系得到坐标值。设计了一种检测轨迹球研磨轨迹系统,通过对实验数据的处理和分析,建立了零偏随温度变化的多项式模型。用建立的多项式模型对零偏进行了实时在线补偿,从补偿的结果可以看出:补偿后的零偏稳定性得到有效提高,在一定程度上满足了工程的需要。对设计的轨迹检测系统在磨球机上进行双自转研磨实验和传统研磨实验,实验结果表明:双自转研磨较传统研磨方式轨迹均匀性好。
[1]Lü B H,Yuan JL,Yao Y X,et al.Study on wear mode of silicon nitride balls in lapping process[J].Key Engineering Material,2005,304-305:403-407.
[2]张树侠,何昆鹏.陀螺仪性能参数表征与评定[J].导航与控制,2010,9(2):33-35.
[3]王志伟.精密球研磨技术的基础研究[D].杭州:浙江工业大学,2005:35-36.
[4]ITG—3200 Product Specification Revision 1.4.InvenSense Inc.
[5]顾广清,夏敦柱,李宏生,等,硅微陀螺仪数字化温度补偿系统的实现[J].舰船电子工程,2008,28(12):49-52.
[6]陈 怀,张 荣,周 斌,等.微机械陀螺温度特性及补偿算法研究[J].传感器技术,2004,23(10):24-26.
[7]西蒙·赫金.自适应滤波器原理[M].4版.北京:电子工业出版社,2003.
[8]尹 文.MIMU微惯性测量单元误差建模与补偿技术[D].长沙:国防科学技术大学,2007:32-41.
[9]赵晓军,伊国兴,王常虹.硅微陀螺仪温度漂移补偿研究[J].传感器与微系统,2008,27(10):48-50.

