双基阵方位—频率匀加速运动目标跟踪算法研究

许兆鹏，韩树平

(海军潜艇学院 水声中心，山东青岛266042)

0 引言

微处理器性能与网络技术的不断提高，解决了多部传感器同步工作和数据传输上的问题，使得多传感器联合使用进行目标跟踪成为一个重要的研究方向，其中，应用两部声纳基阵即双基阵的量测信息对水中运动目标的跟踪问题是研究的热点之一。

匀加速运动是目标较为常见的运动方式，但尚没有基于双基阵量测信息对水中匀加速运动目标跟踪方面的研究，以往的研究只针对匀速直线运动目标［1～4］。这里将双基阵量测的目标方位信息和其中一部基阵量测的目标频率信息作观测融合后，根据匀加速运动状态方程，建立双基阵方位—频率匀加速运动目标跟踪系统。由于该跟踪系统的观测方程中含有非线性函数，则其为非线性系统。此时，对于系统的非线性性，根据量测值应用非线性滤波算法对匀加速运动目标进行状态估计。为此，本文提出了一种双基阵方位—频率匀加速运动目标跟踪算法。

本文又对该跟踪系统的可观测性进行了研究。所谓可观测性，是指系统在忽略观测噪声情况下目标状态是否有唯一解的问题，有唯一解则称系统是完全可观测的。可观测性是跟踪系统进行目标跟踪的前提和基础，只有满足可观测条件才能对系统进行正确求解，从而实现对目标的有效跟踪。以往的研究表明:对于非线性系统的可测性有多种定义方法，而按照线性系统的有关理论，线性系统的可测性具有明确的定义［5］。由于该系统的非线性性，这里拟从线性系统可测性的有关理论出发，通过将双基阵方位—频率匀加速运动目标跟踪系统伪线性化来进行可观测性的研究，得到其可观测性判定条件。最后，通过仿真验证了算法的有效性和可观测性判定条件的正确性。

1 双基阵方位—频率匀加速运动目标跟踪算法

在水中目标被动跟踪问题中，由于跟踪距离远远大于目标深度，可以忽略深度的影响，将目标与双基阵设定在同一平面内，即研究二维的目标被动跟踪问题［6］。为了便于研究，假设双基阵位于同一观测平台，以基阵1为坐标原点建立二维笛卡尔坐标系，基阵2位于x轴，双基阵声学中心的间距为L;采样间隔为T，第k个采样时刻目标以基阵1为基准的相对运动向量为 X(k)=［x(k)，y(k)，vx(k)，vy(k)，ax(k)，ay(k)］T，x(k)，y(k)为 x 方向与 y方向上的相对距离，vx(k)，vy(k)为 x方向与 y方向上的相对速度，ax(k)，ay(k)为x方向与y方向上的相对加速度;α(k)和β(k)分别为双基阵所观测的目标方位，如图1所示，这里假设基阵1观测的目标频率信息为f(k)，目标固有频率为f0。

图1 双基阵跟踪系统Fig 1 Tracking system of two sonar arrays

状态方程为

式中 W(k)为过程高斯白噪声，状态矩阵Φ为

观测方程为

式中 V(k)是量测高斯白噪声，c为声速。

式(1)和式(2)构成了基于双基阵方位—频率的匀加速运动目标跟踪系统。式(2)中含有非线性函数arctan{·}，则此跟踪系统为非线性系统。针对系统的非线性性，依据各采样时刻的量测值，采用扩展卡尔曼滤波(EKF)算法或无迹卡尔曼(UKF)滤波算法等非线性滤波算法［7］，对该系统进行匀加速运动目标状态估计，从而可对匀加速目标进行跟踪，此过程即构成了基于双基阵方位—频率匀加速运动目标跟踪算法。

2 系统可观测性判定

2.1 伪线性化

为了便于系统可观测性判定，将跟踪系统由离散形式改写成连续时间系统的形式，并对观测方程进行伪线性化。需说明的是:在分析过程中并没有考虑噪声的影响，这是因为噪声的存在只对定位和跟踪的精度有影响，而不影响系统的可观测性。状态向量改写为

状态方程改写为式(3)

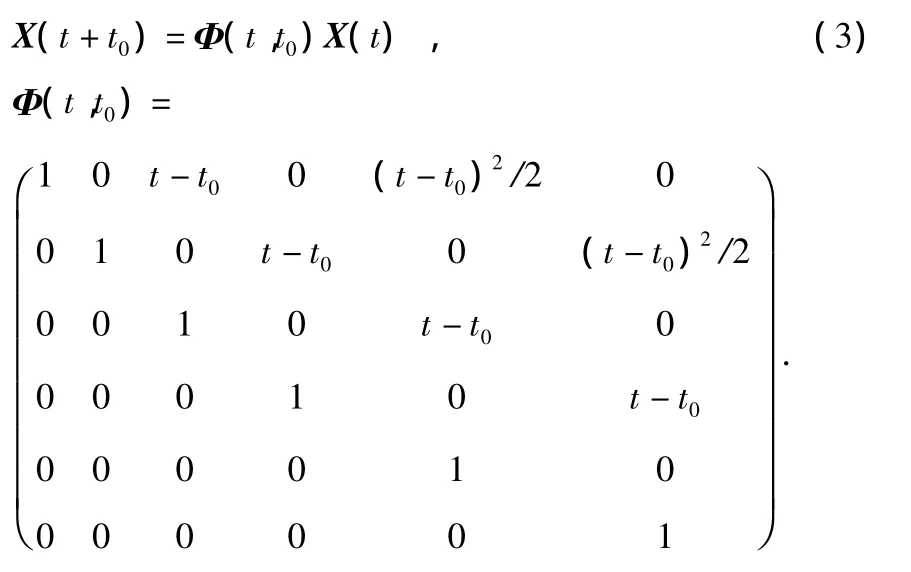
其中，t0为跟踪起始时刻。

采用伪线性处理后［1，2］，量测方程改写为

2.2 可观测性判定条件

这里采用Jaufferet C提出的可观测性判定定理［5］

可观测的充要条件是:∀Y≠0∈Rn，∃t∈［t0，t1］，使得H(t)Φ(t，t0)Y≠0。

该定理又可用其逆否命题表述，可观测充要条件是:∀t∈［t0，t1］，如果 H(t)Φ(t，t0)Y=0，则 Y=0。

其表明系统在时间段［t0，t1］内可观测，当且仅当对任何一个非零向量 Y，总存在 t∈［t0，t1］使得 H(t)Φ(t，t0)Y≠0或者说若 H(t)Φ(t，t0)Y=0，则 Y 必须为0。

若假 设 Y= ［y1，y2，y3，y4，y5，y6，y7］T，则 根 据H(t)Φ(t，t0)Y=0 可得方程组式(5)～ 式(7)

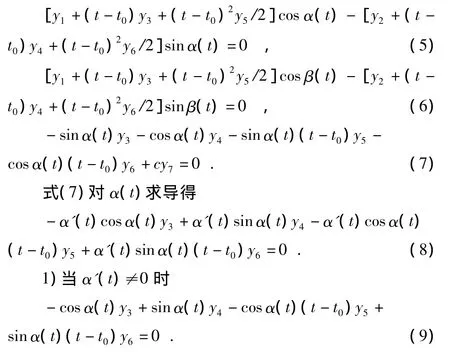
由于α(t)随时间变化，要等式成立只能有y3=y4=y5=y6=0，将它们分别代入式(5)和式(7)可得式(10)和y7=0

由于α(t)随时间变化，要等式成立只能有y1=y2=0。则Y即为零向量，所以，系统可观测，此时只要基阵1测量的方位变化，即可满足条件。

2)当 α'(t)=0时

式(8)恒为零，此时要使式(5)和式(6)组成的方程组有唯一解，则需方程组的行列式值 sin［α(t)-β(t)］不为零，则 α(t)-β(t)≠kπ。此时，由于行列式是随t实时变化的，要使等式成立必有

亦由t-t0随t实时变化，要使等式成立需y1=y3=y5=0和 y2=y4=y6=0，则式(7)中，y7=0。所以，得 Y=0，因此，系统可观测，此时只要目标不在双基阵连线上运动即可满足条件。

综上，双基阵方位—频率匀加速运动目标跟踪系统可观测条件为:只有当匀加速运动目标在双基阵连线上运动，并且用于测量目标频率的基阵所测量的方位值不发生变化时，系统才不可观测外，其余情况均可观测。

3 仿真验证

为使问题简化，假设两部声纳均静止不动，声纳1的坐标为(0，0 km)，声纳2的坐标为(1，0 km)，两声纳方位测量均方误差分别为0.2°和0.3°，声纳1频率测量均方误差为0.5 Hz，目标固有频率为500 Hz，采样周期为2 s;目标初始速度为零，初始位置(-5，0 km)，航向90°，轴向分加速度(ax，ay)初始时为(0.04，0 m/s2)，过坐标原点后变为(-0.04，0 m/s2)，运动时间为1 000 s;采用本文所提方法进行跟踪，滤波时选用UKF滤波算法，Monte—Carlo仿真次数为50，跟踪结果如图2所示。

图2 跟踪结果Fig 2 Results of tracking

从仿真结果可看出:0～500 s，目标在双基阵连线上运动，此时基阵1所测方位 α(t)恒为270°，即 α'(t)=0，不满足可观测条件，跟踪结果不收敛;但当目标经过原点后，α(t)=90°，方位发生变化，α'(t)≠0，此时满足可观测条件，跟踪结果收敛。此外，应用所提出的方法对目标稳定跟踪时的跟踪精度较高。

4 结论

基于双基阵量测的方位信息和其中一部基阵量测的目标频率信息，根据匀加速运动状态方程，建立跟踪系统，进而提出了一种基于双基阵方位—频率匀加速运动目标跟踪算法。从伪线性化角度出发，用线性理论中可观测性判断定理对该跟踪系统进行分析，给出了此系统的可观测性判定条件。最后，通过仿真验证了算法的有效性和可观测性判定条件的正确性。

［1］杜选民，姚 蓝.多基阵联合的无源纯方位目标运动分析研究［J］.声学学报，1999，24(6):605-610.

［2］陈伏虎，胡 青.多阵方位—频率目标运动分析算法研究［J］.声学与电子工程，2003(7):1-5.

［3］关 欣，何 友，衣 晓.双基阵纯方位水下被动目标跟踪性能仿真分析［J］.系统仿真学报，2003，15(10):1464-1466.

［4］曲 毅，刘 忠，屈津竹.基于时延的水中目标纯方位跟踪算法［J］.系统工程与电子技术，2007，29(1):107-109.

［5］胡友峰.非机动水下三维被动目标运动分析研究［D］.西安:西北工业大学，2002:19-22.

［6］刘 忠，周 丰，石章松，等.纯方位目标运动分析［M］.北京:国防工业出版社，2009:77.

［7］郭晓松，李奕芃，郭君斌.贝叶斯目标跟踪方法的研究［J］.计算机工程，2009，35(12):137-139.