神经网络和SVM多传感器融合的隧道CO体积分数研究*

王 芹，王晓东，吴建德，黄国勇，范玉刚

(1.昆明理工大学信息工程与自动化学院，云南昆明650500;2.云南省矿物管道输送工程技术研究中心，云南昆明650500)

0 引言

目前，国内外公路隧道通风控制系统中的传感器布设单一、类型较少、可靠性低，一旦传感器损坏就会对隧道的安全运营造成危害［1］。CO体积分数是隧道环境运行状态的一项重要指标，如果隧道一断面的CO传感器失效，能通过该断面其他相关传感器的数据融合出隧道CO体积分数，对于提高车辆通过隧道安全性能有重要意义［2，3］。多源信息融合技术对多传感器获得信息进行协调、组合、互补来提高系统有效性，比单一传感器更精确、可靠［4］。

神经网络记忆性和强大的非线性映射能力，在信息融合中引起广泛的重视。神经网络信息融合主要成果有:Melgani F等人设计多层前馈神经网络将遥感图像空间信息、时间信息和光谱信息融合;Cao Jin利用BP神经网络设计了多源信息融合机器人导航系统等［5］。但神经网络信息融合存在不足，基于经验的风险最小化，泛化能力低、易陷入局部极值、训练学习速度较慢、对小样本数据分析能力低。而支持向量机(SVM)信息融合基于结构风险最小化原则，泛化能力强，具有全局最优性，是小样本统计学习理论［6，7］。本文分别比较了 BP，RBP 神经网络、SVM 融合隧道CO体积分数模型效果和不同组合的最优加权融合模型CO体积分数效果，结果表明最优加权融合避免了单一融合模型的信息缺陷，实现优势互补，提高融合CO体积分数的精度。

1 多源信息融合系统结构

1.1 输入数据选取

输入数据选取要与隧道CO体积分数变化相关因素，一般隧道CO主要是隧道内的行驶车辆所排放出来的，因此，主要与车速、车流量关系比较大，同时还与隧道能见度(如发生火灾)、风速等因素有关系，所以，选取车速(v)、车流量(TV)、能见度(VI)、风速(w)为融合系统的输入量。

1.2 神经网络融合系统

目前有多种不同的神经网络模型被应用信息融合，如BP神经网络、径向基函数RBF神经网络等。

神经网络模型具有高度非线性映射能力，通过输入前向传播实现由输入到输出的非线性映射，这就正好满足信息融合隧道CO体积分数的要求［8］。

1.2.1 BP神经网络融合算法

BP神经网络理论上证明具有三层网络能实现任意非线性逼近映射。本文BP网络融合三层网络，输入层神经元为4，隐含层神经元为10，输出层神经元为1，隐含层采用S型正切传递函数，输出层采用线性传递函数。本文采用BP网络的误差反向传播算法，思想是将网络输出与期望输出间的误差归结为权值和阈值的“过错”，调整权值和阈值使误差沿着下降最快的方向变化。

1.2.2 RBF神经网络融合算法

RBF网络基本思想:用径向基函数作为隐含层节点的“基”构成隐含层空间，将低维的输入数据映射到高维空间内;然后通过线性函数将隐含层节点输出数据映射到输出层节点。为使计算方便隐含层采用RBF高斯激活函数，隐含层到输出层使用线性传递函数［9］。由此可得信息融合输入与输出表达式为

其中，wi，θ分别是隐含层到输出层的权值和阈值;y为隧道CO体积分数融合输出值。RBF网络的学习过程分为2个阶段。第一阶段，根据输入样本确定中心向量，标准化常量。第二阶段，根据最小二乘法求权值和阈值，进一步提高进度。

1.3 SVM信息融合系统

SVM应用于信息融合基本思想是寻找一个最优分类面使得训练样本离该最优分类面误差最小，设有l训练样本对为{(xi，yi)，i=1，2，…，l}，其中，xi是第 i只传感器数据作为训练样本的输入列向量，yi为对应的融合输出。在高维特征空间中建立最优的线性回归函数为

其中，φ(x)为非线性映射函数。现在的问题成为，根据已知的l个样本，确定向量w和标量b。对于这样一个回归问题，基于SVM的最优回归函数是指满足结构风险最小化原理，其最小化表示为

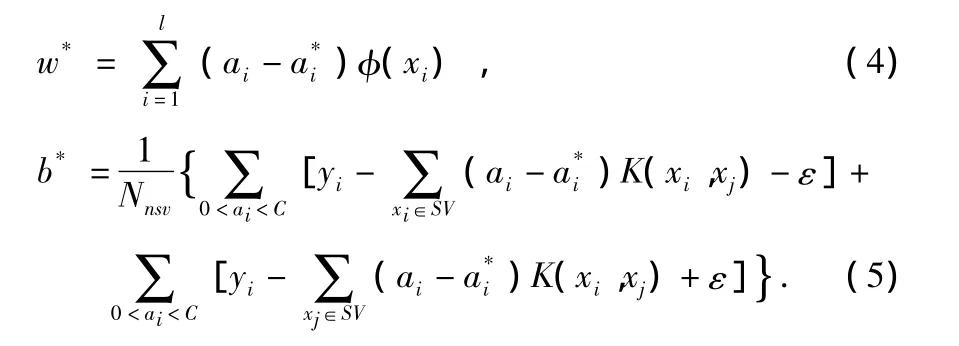
其中，Nnsv为支持向量个数，K(xi，x)为核函数 SVM 的核函数有多种形式有多项式核、RBF核函数等。本文使用的核函数为

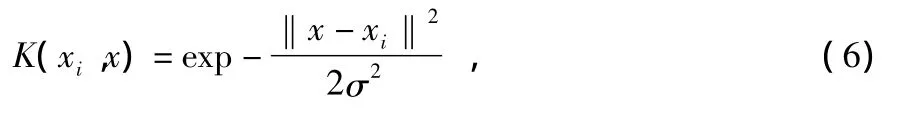
于是基于SVM的信息融合的输入与输出的关系式为

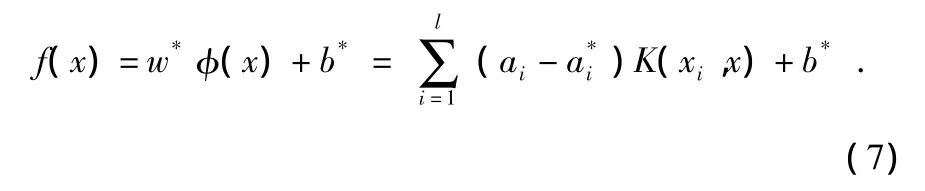
其中，只有部分参数(ai-a*i)不为零，其对应的样本为支持向量。可以看出与神经网络不同，SVM的拓扑结构是由SVM决定，避免了神经网络反复试凑确定网络结构问题。SVM利用非线性变换将原始输入变量映射到高维特种空间，在高维空间中进行信息融合，还保证了融合具有良好的泛化能力［10］。SVM的训练算法最终可以转化为QP规划问题，当训练样本少时可以用牛顿法、共轭梯度法，当训练样本大时可以使用分块算法理论、Osuna算法、SMO序列最先优化算法等［11］。

1.4 均方误差最优加权信息融合

多源信息融合技术中加权融合是一种经典的信息融合方法被受重视。本文用最优均方误差加权融合算法，该方法是对BP，RBP神经网络和SVM融合结果进行再次加权组合融合，其融合精度高于单一融合。理论证明最优均方误差加权融合能使融合后输出值均方误差最小，且小于参与单一模型融合的均方误差［12］。设有m种融合系统的最优均方误差可以表示

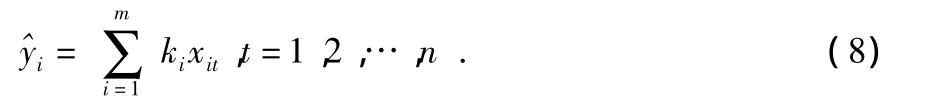
其中，xit为第i个融合系统在第t个样本输出值记，^yt为第t个样本加权融合值，ki为第i只传感器的权系数，且满足，设yt为第t个样本的真实值，加权融合输出的第t个样本的误差为

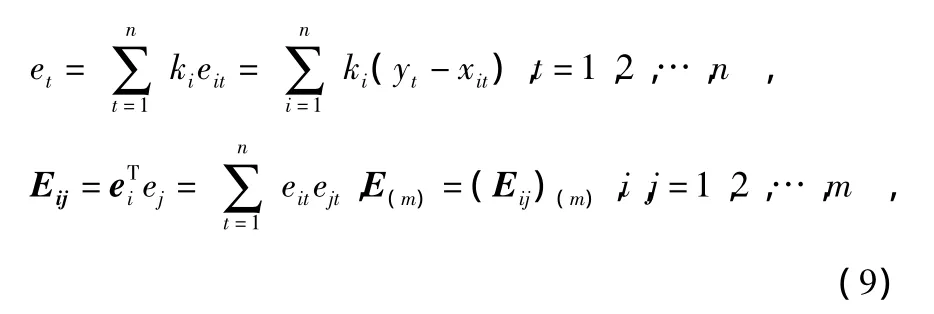
式中 Eij为第i个融合系统和第j个融合系统的均方误差，E(m)为融合输出误差信息方阵。寻找权系数向量K*，使组合预测方法的预测均方误差J达到极小值Jmin，则称为最优均方误差加权融合，由此可以转化为下列最优化问题

根据Lagrage求条件极值可求出K*，Jmin，可得最优加权系数为

1.5 冗余度的最优加权融合有效性分析

最优加权融合是对不同单一融合模型信息进行选择利用的过程。如何选择参与加权的单一融合模型，才能充分发挥各单一融合模型互补信息，使最优加权融合精度大幅提高。对不同单一融合模型是通过不同结构融合CO体积分数信息，因此，单一融合模型输出可看作是同一目标发出的信息源，这就可用信息论方法进行分析，设2种单一融合模型输出为 Y1，Y2，Y1所含的隧道 CO体积分数信息熵H(Y1)可分为两部分，第一部分Y1，Y2所共有的CO体积分数信息熵R既冗余信息，第二部分HY2(Y1)为Y1所特有的CO体积分数信息熵，因此，可得2种单一融合模型输出Y1，Y2之间冗余度R为

其中，HY2(Y1)=为两单一融合输出相关性分布。通过分析冗余度与最优加权融合效果可找到之间的规律。用该规律对参与加权融合的单一融合模型进行筛选，找到提高最优加权融合精度明显的组合。

2 仿真实验与结果分析

为了验证信息融合模型的有效性。本文采用某公路隧道监控系统中同一断面的车速、车流量、能见度、风速为融合系统输入量，隧道CO体积分数为融合系统输出量。为不失一般性，每次实验用计算机对100组样本随机的抽取80组样本作为神经网络和SVM的训练集，余下的20个样本作为对模型的测试集。

2.1 信息融合模型性能评价指标

为了评价不同融合模型的融合精度，本文选用均方误差(MSE)和相关系数P对融合模型性能进行评价。计算公式如下

MSE越小说明模型性能好，相关系数在［0，1］内，接近1表明模型性能好;相反，则差，一般大于0.8，说明模型具有融合能力，大于0.9说明模型具有较好的融合效果。

2.2 单一融合系统结果分析

BP，RBF神经网络及SVM 3种单一融合模型融合结果比较如表1和图1所示。3种融合模型P都大于0.8表明都能对隧道CO体积分数进行融合。BP网络融合精度最差，P最小，MSE值最大;RBF网络融合精度一般，P一般，MSE值比BP网络降低30%;SVM在单一融合模型中融合精度最好P高于0.9，MSE值最小，分别比BP网络和RBF网络降低了48%和25%，可见SVM具有全局最优性。

表1 单一融合模型性能指标比较Tab 1 Performance index comparison of single fusion model

图1 单一融合模型融合效果对比Fig 1 Fusion effect comparison of single fusion model

2.3 最优加权融合结果分析

本文将BP网络、RBF网络与SVM两两加权融合和3种全部加权融合进行比较研究。比较结果如表2和图2所示。

图2 不同组合最优加权融合效果对比Fig 2 Optimal weighting fusion results comparison of different combinations

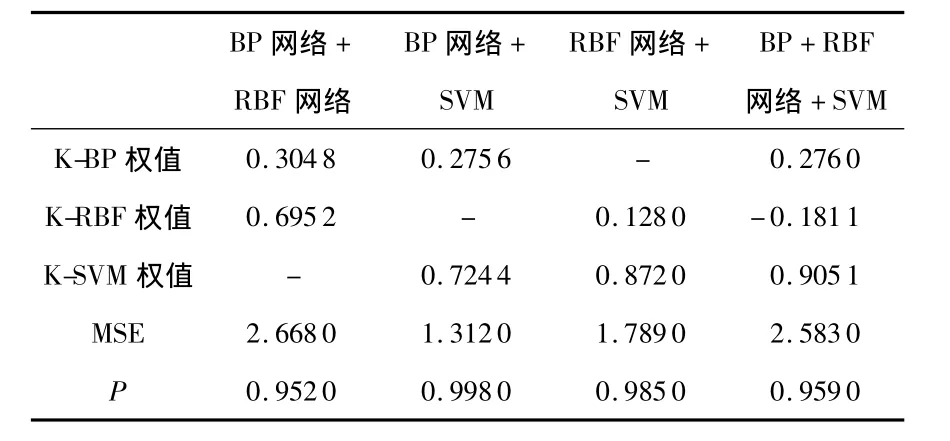
表2 不同组合最优加权融合模型性能指标比较Tab 2 Optimal weighted fusion model performance comparision of different combinations

对比表1和表2可以看出:加权融合精度比单一融合精度都有不同程度提高，表明加权融合对不同单一融合信息进行选择利用，P值都在0.95以上具有较好的融合效果。BP网络与SVM加权融合精度最高，P值为0.998，MSE值比单一BP网络和SVM分别降低81%和63%，精度有大幅提高;虽然单一的RBF网络和SVM融合精度高，但是RBF网络与SVM加权融合精度不是最高，P值为0.985，MSE值比单一RBF网络和SVM分别降低63%和50%，精度提高很明显;BP网络与RBF网络加权融合精度最低，P值为0.952，MSE值比单一BP网络和RBF网络分别降低61%和25%，精度有提高;3种全部加权融合仅比BP网络与RBF网络加权融合P值仅提高0.007，MSE值仅降低3%精度提高不明显。由图3可以看出:BP网络与SVM的加权融合预测曲线和真值曲线接近重合，在曲线变化快的区域精度改善明显。

2.4 最优加权融合冗余度分析

由式(12)可计算出单一融合BP、RBF网络，SVM模型两两之间输出CO体积分数的冗余度结果如表3所示，如果某2个单一融合模型之间的冗余度较大，则说明该模型输出信息的关联性大，冗余信息量大。

由表3看出:BP网络与SVM冗余度最低小于5;RBF网络与SVM冗余度其次高于5，BP与RBF网络冗余度最大高于10。根据以上分析，可得如果单一融合模型之间冗余度较低，则加权融合精度提高明显，如SVM分别与BP，RBF网络，虽然单一RBF网络和SVM融合精度高，但是它们之间冗余度大于5，而BP网络与SVM冗余度小于5，所以，RBF网络与SVM加权融合精度提高不是最大;如果单一融合模型之间冗余度较高，则加权融合精度提高不明显，如BP与RBF网络，SVM 3种全部融合。由于神经网络与SVM融合结构不同，输出CO体积分数冗余信息相对少，加权融合综合了神经网络和SVM的各自优点，实现优势互补，因此，加权融合精度提高明显;BP与RBF神经网络融合结构近似，输出CO体积分数冗余信息相对大，因此，加权融合精度提高不明显。3种全部加权融合的精度没有明显提高，是因为RBF网络分别与BP网络和SVM的冗余度比较大，所以，RBF网络的权值小且为负值-0.1811，说明对提高精度影响非常小，它只提供冗余信息，应该将它删除。

表3 单一融合模型输出之间冗余度Tab 3 Redundancy between single fusion the model output

3 结束语

本文将BP，RBF神经网络，SVM融合及最优加权融合模型应用于公路隧道CO体积分数。研究表明3种单一融合模型的有效性，在单一模型中SVM融合精度最高;对3种单一融合模型进行组合最优加权融合，发现BP网络与SVM加权融合精度最高，说明加权融合充分发挥了神经网络非线性逼近能力、记忆能力和SVM全局最优性，弥补了单一神经网络融合易陷入局部极值的不足;不同单一组合加权融合对融合精度影响大。冗余度小时加权融合才能实现信息互补，达到提高融合精度的目的。

［1］李家龙.公路隧道通风节能技术研究［D］.重庆:重庆交通大学，2007.

［2］夏永旭.我国长大公路隧道通风中的几个问题［J］.公路，2003(5):147-149.

［3］杨兆升.基础交通信息融合方法综述［J］.公路交通科技，2006，23(3):111-116.

［4］王耀南.多传感器信息融合及其应用综述［J］.控制与决策，2001，16(5):518-522.

［5］周呜争，汪 军.基于SVM的多传感器信息融合算法［J］.仪器仪表学报，2005，26(4):407-410.

［6］Capparuccia R，Leone R D，Marchitto E.Integrating support vector machine and neural network［J］Neural Networks，2007，20(5):590-597.

［7］韩崇昭，朱红艳，段战胜.多源信息融合［M］.北京:清华大学出版社，2010.

［8］Inguva R，Johnson J L，Scham SM P.Multi-feature fusion using pulse coupled neural networks［J］.SPIE，1999，3719:342-351.

［9］Leonard JA.RBF network for classifying process faults［J］.Control Systems，1991，23(4):31-38.

［10］Pouteau R，Stoll B，Chabrier S.Multi-source SVM fusion for environmental monitoring in Marquesas archipelago［J］.Geoscience and Remote Sensing Symposium，2010，26(6):2719-2722.

［11］白 鹏，张喜斌，张 斌，等.支持向量机理论及工程应用实例［M］.西安:西安电子科技大学出版社，2008:13-73.

［12］李 伟，何鹏举，高社生.多传感器加权信息融合算法研究［J］.西北工业大学学报，2010，28(5):674-679.