双轴旋转惯导系统的转位方案优化技术研究*

朱 蕾，袁书明，程建华

(1.海军装备研究院舰船所，北京100073;2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

0 引言

旋转调制捷联惯导系统通过旋转机构的引入，实现了惯性器件误差的有效调制，大大提高了捷联式惯导系统的导航定位精度，在国内外高精度舰船导航领域得到了大量的应用，如美国SPERRY公司的MK39单轴旋转捷联惯导和 MK49 双轴旋转捷联惯导系统［1～3］。

单轴旋转方式由旋转机构提供一个转轴用于惯性器件误差的调制，这种方案结构简单、易实现、成本低，目前仍是应用较为广泛的旋转调制方案。但由于单轴旋转方案无法实现三轴器件误差调制，因此，未从根本上解决惯导系统定位误差随时间积累的问题。而双轴旋转捷联惯导由于能够调制三轴惯性器件误差，因此，具备了从根本上抑制惯导系统误差随积累的特性［4］。

转位方案是影响旋转调制效果的重要因素，一直是国内外学者在旋转式捷联惯导系统方案设计的重要研究内容。不仅如此，在同类转位方案中，转位方式、转位次序和转位速率的不同，也会产生不同的调制效果。

双轴依次旋转调制方案是目前国内外学者最多采用和研究的一种方案，但在方案研究和设计过程中，多数文献仅分析旋转方案对器件误差的调制效果，未从定量角度分析转位方案的细节参数对系统定位性能的影响［5，6］。

基于此，本文就双轴依次旋转捷联惯导系统方案，就转位过程中的旋转、停止时间对定位性能影响开展研究，通过对定位性能的分析改进转位方案，达到提高捷联惯导系统精度的目的。

1 双轴依次旋转的误差调制效果分析

1.1 双轴依次旋转惯导原理

陀螺仪和加速度计是惯性导航系统的2个核心惯性器件，二者的精度决定了惯性导航系统的位置、速度和姿态精度。而从频域角度分析惯性导航系统特性可知，惯导系统具有对高频干扰衰减的特性，即具有较高频率的周期干扰作用在低通特性的系统上，漂移造成的误差将大为减小，旋转式惯导系统正是利用了这一特性，将常值误差调制为高频误差，提高系统精度。

双轴依次旋转惯导系统通过引入具有2个旋转自由度的旋转机构进行惯性元件误差调制，常用的八位置双轴依次旋转方案如图1所示［7］。

图1 双轴依次旋转效果图Fig 1 Effect diagram of double-axis rotation sequences

图1中，箭头指向代表旋转轴指向，各旋转次序的旋转时间为tr，在各位置的停止时间为ts。

依据图1可得八位置双轴依次旋转惯导系统的转动次序为:

次序1:绕东向轴正转180°由A到位置B停止;

次序2:绕天向轴正转180°由B到位置C停止;

次序3:绕东向轴反转180°由C到位置D停止;

次序4:绕天向轴反转180°由D到位置A停止;

次序5:绕天向轴正转180°由E到位置F停止;

次序6:绕东向轴反转180°由F到位置G停止;

次序7:绕天向轴正转180°由G到位置H停止;

次序8:绕东向轴正转180°由H到位置E停止。

1.2 漂移调制效果分析

为简化问题分析，设初始时刻，框架坐标系oxryrzr、载体坐标系oxbybzb和地理坐标系oxtytzt重合，由此可计算出8个转动次序过程中的陀螺等效漂移为

依据旋转次序、变换矩阵Tbr和式(1)，可以求得沿地理系的等效漂移如图2～图4中实线所示。

图2 等效东向陀螺漂移Fig 2 Drift curve of the equivalent east gyro

图3 等效北向陀螺漂移Fig 3 Drift curve of the equivalent north gyro

图4 等效天向陀螺漂移Fig 4 Drift curve of the equivalent up gyro

传统的分析方法是对等效漂移在一个周期内累加，只要等效陀螺漂移累加和为零，就表示旋转方案实现了对器件误差的旋转调制［7，8］。但对图2～图4的等效漂移曲线进行分析可知，即使在一个旋转周期内三轴漂移的累积和为零，但对于不同的旋转时间tr和停止时间ts，等效漂移的变化规律是不同的，其对惯导系统误差的影响也是不相同的。

2 双轴旋转方案的定位误差分析

2.1 基于傅里叶级数变换的定位误差推导

对于双轴旋转方案的定位误差分析，采用先对漂移做拉氏变换代入误差方程，而后进行拉氏反变换得到时域表达式的方法，其求解过程非常繁琐。为此，首先对等效漂移进行简化，在不影响调制漂移基本特性的前提下，得到如图2～图4中虚线所示的漂移曲线，即将3个方向的等效漂移简化为方波形式。

根据静基座下的捷联式惯导系统误差方程，可以得到受漂移误差激励的系统经纬度误差表达式为

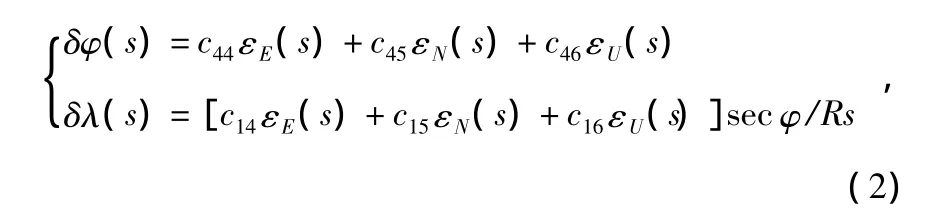
式中 δφ，δλ 分别为纬度误差和经度误差，c14～c16与 c44～c46均为已知量［8］。

对于如图2～图4所示的等效陀螺漂移，无法直接代入式(2)直接求解经纬度误差。为此，对简化后的等效漂移进行傅里叶级数展开，得到

通过对式(6)进行拉氏变换，代入式(2)后通过拉氏反变换运算，即可得到双轴依次旋转方案的定位误差时域表达式。

2.2 不同转位方式下的定位误差分析

为分析不同旋转时间tr和停止时间ts对系统定位误差的影响，对 tr≈ts，tr≪ts和 tr≫ts三种情况下的定位误差进行分析。

1)tr≈ts情况

考虑到旋转周期8(tr+ts)≪Ts(舒勒振荡周期)，可以简化得纬度、经度误差时域输出为

2)tr≪ts情况

简化后的纬度、经度误差时域输出为

3)tr≫ts情况

简化后的纬度、经度误差时域输出为

通过对式(7)～式(11)的输出可以看出:在陀螺漂移的激励下，纬度误差和经度误差中仅包含常值和振荡误差项，没有随时间增长的趋势项。而由式(11)可知，当tr≫ts时，被激励纬度和经度误差已不包含与北陀螺εy有关的误差项，而且，将式(11)与其他2种情况的误差项幅值相比，式(11)中的经纬度误差项幅值远小于tr≈ts和tr≪ts情况下的经纬度误差幅值。

3 计算机仿真

仿真条件设置如下:

陀螺漂移:εx=0.01°/h，εy=0.01°/h，εz=0.01°/h;

对称标度因数误差阵

非对称标度因数误差阵

安装误差阵

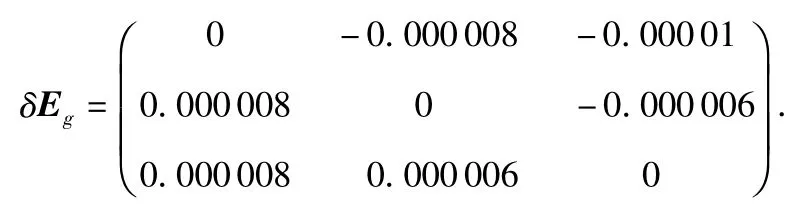
初始位置:φ0=45.78°，λ0=126.6705°;

旋转周期:取旋转角速度为3°/s。

1)tr=ts=1 min:系统在每个停止位停留1 min，在2个停止位间旋转时间为1min，系统定位误差曲线如图5所示。

图5 仿真条件1激励的定位误差曲线Fig 5 Positioning error curve excited by simulation condition 1

2)旋转系统无停止时间，旋转时间为tr=1 min:系统没有停止位，在每个改变旋转轴的位置间旋转时间为1 min，

式中 εE，εN，εU为沿地理坐标系轴向的等效陀螺漂移，εx，εy，εz为沿 x，y，z陀螺敏感轴的陀螺漂移，T=tr+ts。

考虑到惯导系统为一低通滤波器，为简化推导分析过程，对简化后的等效漂移进行傅里叶级数展开，提取其级数展开式频率最低的基波误差信号，得到系统定位误差曲线如图6所示。

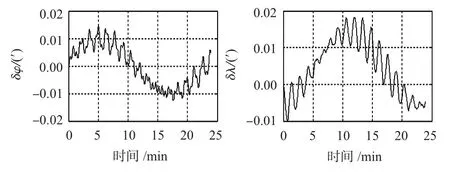
图6 仿真条件2激励的定位误差曲线Fig 6 Positioning error curve excited by simulation condition 2

通过不同转位方式下的经纬度误差分析和仿真分析可知:

1)减小系统在停止位停留时间，即惯性测量单元在一个旋转周期内，旋转周期长于停止时间，常值漂移激励的经纬度误差越小;

2)尽量减小旋转周期。在双轴旋转方案中，常值漂移激励的经纬度误差正比于系统旋转周期，旋转周期越长，则激励的经纬度误差越大。

4 结论

针对双轴旋转调制捷联惯导受旋转方案影响的问题，对旋转方案的误差特性开展了定量推导分析。结合仿真，明确了转、停时间对系统经纬度误差的影响关系，在此基础上给出了转位方案的优化改进方法，为设计提高双轴旋转捷联惯导经度提供了参考依据。

［1］张炎华，王立瑞，战兴群，等.惯性导航技术的新进展及发展趋势［J］.中国造船，2008，10(49):134-141.

［2］Tucker L E.The AN/WSN—7B marine gyrocompass/navigator［C］∥ION NTM，2000:348-357.

［3］Hibbard R，Wylie B，Levison E.Sperry marine MK—49，The world’s best ring laser gyro ship’s inertial navigation system［C］∥JSDE Proceedings，1996:35-46.

［4］程建华.光纤陀螺捷联惯导系统监控技术研究［D］.哈尔滨:哈尔滨工业大学，2009:24-25.

［5］翁海娜，陆全聪，黄 昆，等.旋转式光学陀螺捷联惯导系统的旋转方案设计［J］.中国惯性技术学报，2009，17(1):8-17.

［6］孙 枫，孙 伟，郭 真.基于IMU旋转的捷联惯导自补偿方法［J］.仪器仪表学报，2009，30(12):2511-2517.

［7］袁保伦.四频激光陀螺旋转式惯导系统研究［D］.长沙:国防科学技术大学，2007:56-67.

［8］袁保伦，饶谷音.光学陀螺旋转惯导系统原理探讨［J］.国防科技大学学报，2006，28(6):76-80.

［9］张树侠，孙 静.捷联式惯性导航系统［M］.北京:国防工业出版社，1992:55-60.

［10］Wang Xinzhe，Zhao Lin.The research on rotation self-compensation scheme of strapdown inertial system［C］∥ICMA，2009:4760-4764.