多传感器系统估计的稳健切比雪夫中心估计融合*
屈小媚
(西南民族大学计算机科学与技术学院,四川成都610041)
0 引言
多传感器信息融合是将来自多信息源的数据和信息加以智能化的合成,产生比单一传感器更精确、更完整、更可靠的描述和判断,是一个涉及信息科学、计算机科学、自动化科学的复合型学科。它的结构模型主要有4种形式:分布式、中心式、混合式和分级式。这4种结构的信息融合的理论研究均已取得了很大进展。
文献[1~3]针对多传感器数据的融合问题进行了研究,这些研究基于一个重要假设,即多传感器信息融合的数学模型是精确知道的。然而,在实际应用中,不论军事还是民用方面,多传感器信息融合的数学模型常常是不准确的。在多传感器分布式系统中,当观测噪声范数有界的情况下,如何得到系统参数估计的稳健估计融合是多传感器信息融合领域中一个受到广泛关注的研究方向[4~8]。解决这类问题的常用方法是最小二乘法[4],即求使得估计误差的范数最小的参数估计,其中范数取欧几里德范数。最小二乘在本质上是确定性的方法,因为并未对各变量假设任何统计性质。当一些统计信息(比如观测噪声的方差)已知,可以用加权最小二乘。但当出现异常值时,现有的许多估计方法表现出不稳健的现象,模型的解不一定是在估计绝对误差意义下最好的估计。特别是当观测矩阵是病态的时候,可能得到很差的估计。虽然很多方法试图寻找有偏且是更接近真实参数z的估计,但是都不一定能使得估计的绝对误差小,参见文献[5~7]。
本文的主要策略是:首先描述出未知参数z的可行集合,为线性系统的所有可行解,命名为可行参数集(feasible parameter set,FPS)。然后选择FPS的一个使得估计绝对误差稳健的中心来作为融合的估计,即切比雪夫中心。
然而,一般情况下,求一个凸集的切比雪夫中心是一个很难的问题,核心的困难在于里层的极大问题非凸。对于这个问题,文献[8]提出了一个松弛的切比雪夫中心方法。本文的主要目的在于建立另外一种策略来求解FPS的切比雪夫中心。虽然这个问题在一般情况下很难,但是有2个例外情况[9,10]:一是 FPS是多面体,且包含 FPS的球是l∞范数下的球;二是FPS是有限集。本文主要利用后面一种情况,因为可以证明:在二维情况下,即z∈R2时,FPS的切比雪夫中心等价于有限个特殊点的切比雪夫中心。在高维情况下,近似的切比雪夫中心则通过投影到二维平面的方法得到。
1 多传感器系统估计的稳健切比雪夫中心融合
考虑如下的多传感器系统中确定性参数z的参数估计问题
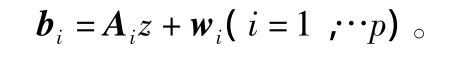
其中,Ai是已知的矩阵,wi是范数有界的噪声。为了得到使得估计绝对误差小且稳健的估计融合,首先描述出未知参数z的可行集合,为线性系统的所有可行解,命名FPS

式中 ρi为噪声wi的范数的上界。
可行参数集的切比雪夫中心可以通过如下的minimax优化问题定义

切比雪夫中心的几何意义是包含集合FPS的最小球(圆)的中心,即使得FPS上的最坏情况下的估计误差最好的点。本质上来说,这是一个优化问题,目标函数为估计的绝对误差,而非数据误差。
2 二维切比雪夫中心估计融合的求解
为了得到参数在最坏估计误差最好意义下的稳健估计,需要求解FPS(1)的切比雪夫中心。图1是2个椭圆的交集的切比雪夫中心的一个例子,其中虚线的圆是最小的包含实线椭圆的交集的圆。
松弛的切比雪夫中心方法是首先将内层的非凸极大问题松弛为对偶问题,再解对应的凸优化问题。关于松弛切比雪夫中心(RCC)方法的细节可参考文献[8]。这种方法得到的切比雪夫中心不是严格的切比雪夫中心。下面的定理1给出在二维情况下,FPS的切比雪夫中心等价于几个特殊点的切比雪夫中心:
定理1 设E1和E2为二维平面上的2个相交椭圆,Xi(i=1,2,3,4)为交点。如果E1和E2的相交区域包含k个长轴上的顶点,记为Dj(j=1,…,k),那么,E1和 E2的相交区域的切比雪夫中心与集合 Xi(i=1,2,3,4)∪Dj(j=1,…,k)的切比雪夫中心是等价的。

图1 两个椭圆交集的切比雪夫中心Fig 1 Chebyshev center of the intersection of two ellipses
3 高维近似切比雪夫中心的算法


式中 A+i为矩阵Ai的广义逆。并且,每一个投影FPSk,l(k≠l)都是非空的,因为它至少包含一个内点,即真实参数 z的投影 zk,l。所以,FPSk,l仅仅表示的是二维平面上椭圆的交,FPSk,l的切比雪夫中心可以通过定理1求得,记为^zk,l,对应的半径记为 ^rk,l。

取高维情况的ACC为式中zk=zk,lk,使得
这样选取ACC的原因是,FPS在各个坐标平面的投影的切比雪夫中心反映了投影的中心位置,即在该平面最小的最坏情况的估计误差,因此,ACC选取对应的每一维上的最小的最坏情况的估计误差。
算法1高维情况下求ACC的算法
1)令z=0n,k=1,l=2,将 FPS 表示为式(3)的形式;
2)按照式(4)表示出FPS的投影FPSk,l;
3)计算出FPSk,l里面椭圆的交点,并选出包含在椭圆的交里的长轴顶点,记这些点的集合为Xk,l;
4)求解下面的凸优化问题
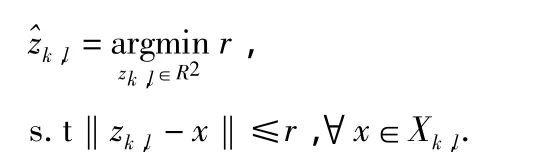
若 l≤n-1,令 l=l+1,回到步骤(2),否则,若 k<n-1,令 k=k+1,l=k+1,回到步骤(2);
5)按照式(5)计算zACC。
ACC融合算法的计算复杂度集中在步骤(4)上,需要求解一个二次约束的线性规划。因此,将原始的非凸优化问题式(2)近似成n(n-1)/2个凸优化问题,其中的每一个都可以高效的求解。所以,在未知参数z的维数不是很高的情况下,这里建议用ACC融合估计方法。
4 数值例子
下面通过模拟例子来比较ACC融合估计方法,RCC融合估计方法以及最小二乘方法。
例1 考虑一个未知参数为二维的两传感器的例子,真实参数z=[1,1]',各传感器的观测由下面的线性模型产生

其中,矩阵Ai∈R5×2的各个元素均由均匀分布随机产生,观测噪声wi的各个分量服从标准正态分布,观测噪声的范数的上界选为 ρ‖σwi‖2,ρ=5。表1为随机采样100次后得到的平均融合估计误差的平方‖z-z‖2(z是zRCC,zACC或者 zLS)。
表1的结果说明:ACC融合估计方法的平均估计误差要低于RCC方法,并且LS估计方法的平均估计误差最大。这是因为在二维情况下,ACC融合方法是精确的FPS的切比雪夫中心,RCC是松弛的切比雪夫中心。而ACC和RCC都是关于优化估计性能的方法,LS则是基于最小数据误差得到的估计,因此,LS估计方法的平均估计误差是最大的。

表1 三种融合方法的估计误差的比较Tab 1 Comparison of estimation error of the three fusion methods
例2 考虑未知参数是三维的情况,即 z=[111]'。2只传感器的观测也由线性模型产生,Ai∈R7×3,其他参数与上面的例子相同。表2为该模型随机采样100次后得到的平均融合估计误差的平方‖z-z‖(z是 zRCC,zACC或者zLS)。
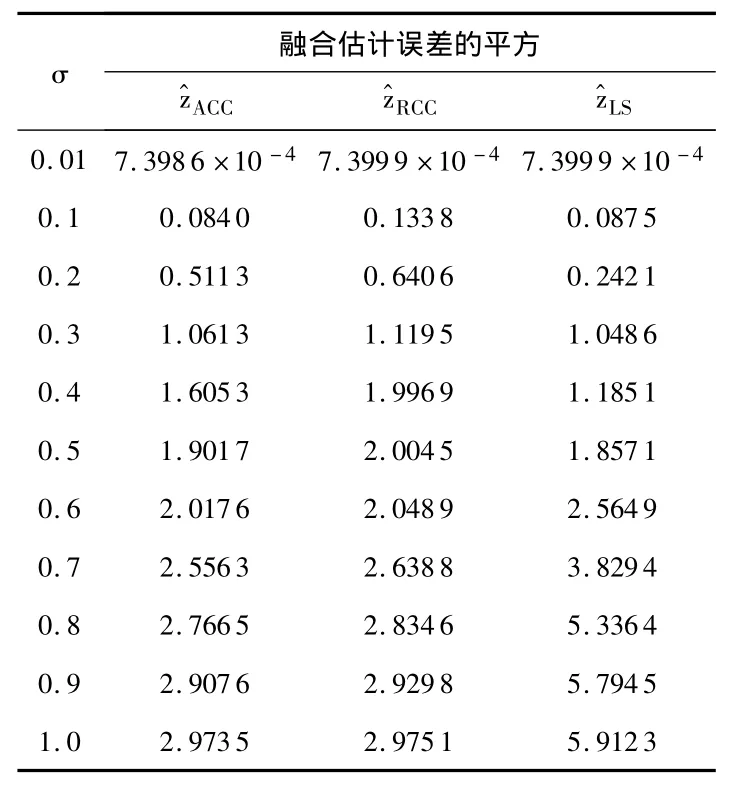
表2 三种融合方法的估计误差的比较Tab 2 Comparison of estimation error of the three fusion methods
通过表2的结果可以得出:尽管ACC和RCC分别为FPS近似的切比雪夫中心估计融合和FPS松弛的切比雪夫中心估计融合,但从平均估计误差来看,ACC方法要优于RCC方法。
5 结论
本文主要针对多传感器参数估计的融合问题,基于稳健融合的策略,将未知参数的所有可行点作为估计范围,然后选取它的切比雪夫中心作为估计的融合。然而,求解一个集合的切比雪夫中心是一个非常困难的问题。本文首先证明了在二维情况下,切比雪夫中心可以精确求解。对于高维情况,采取投影到各坐标平面再融合的方法,得到一个近似的切比雪夫中心作为多传感器估计的融合。数值模拟的结果说明:在多传感器估计融合问题中,提出的ACC融合方法优于已有的RCC融合方法。
[1]唐骥锋,刘国栋.基于多传感器融合的机器人蒙特—卡洛定位决策[J].传感器与微系统,2012,31(3):18-21.
[2]孟秀峰.一种多传感器信息融合的优化方法[J].传感器与微系统,2010,29(12):67-68.
[3]万树平,潘 鹏.基于信息熵的多传感器数据的融合方法[J].传感器与微系统,2008,27(5):64-68.
[4]Kailath T.Lectures on linear least-squares estimation[M].Springer-Verlag,New York,1976.
[5]Eldar Y C,Ben-Tal A,Nemirovski A.Robust mean-squared error estimation in the presence of model uncertainties[J].IEEE Trans on Signal Process,2005,53(1):168-181.
[6]Ben-Haim Z,Eldar Y C.Maximun set estimators with bounded estimation error[J].IEEE Trans on Signal Processing,2005,53(8):3172-3182.
[7]Milanese M,Tempo R.Optimal algorithms theory for robust estimation and perdiction[J].IEEE Trans on Automat Control,1985,30(3):730-738.
[8]Beck A,Eldar Y C.Regularization in regression with bounded noise:A Chebyshev center approach[J].SIAM J Matrix Anal Appl,2007,29(2):606-625.
[9]Beck A,Eldar Y C.Strong duality in noncovex quadratic optimization with two quadratic constraints[J].SIAM J Optim,2006,17(3):844-860.
[10]Xu S,Freund M,Sun J.Solution methodologies for the smallest enclosing circle problem[J].Comput Optim Appl,2003,25(2):283-292.

