基于复合双基阵的弹丸落点观测声定位方法
郑 坚,张炳文,熊 超
(军械工程学院 火炮工程系,石家庄 050003)
基于复合双基阵的弹丸落点观测声定位方法
郑 坚,张炳文,熊 超
(军械工程学院 火炮工程系,石家庄 050003)
基于单基阵的弹丸落点声定位方法存在定距误差大且定向误差小的缺点,针对此问题,利用双基阵交叉定位实现了落点定位。针对双基阵落点定位方法存在一定盲区的不足,提出了一种基于复合双基阵的弹丸落点观测声定位方法。以五元十字阵为复合阵列的基本单元,建立双基阵以及复合双基阵的数学模型,并对定位算法和定向、定距精度进行了理论推导和仿真分析,进行了外场模拟实验。实验结果表明:基于复合双基阵的弹丸落点声定位方法能够有效实现全区域的声定位,相对方位角误差和距离误差均小于4%,定位精度较高。
弹丸;落点定位;五元十字阵;声学;复合双基阵
在射击试验中,弹丸落点位置的确定是整个过程中至关重要的一个环节,落点散布和射击误差的计算准确度和可信度直接取决于落点的精确定位。目前靶场较为常用的落点定位方法有光学法和人工搜索法。其中,光学法的原理是利用光学仪器判读落点角度,并结合基站坐标进行坐标转换,确定弹丸的位置,这存在一定的判读误差,且受天气条件及靶场地形区域的影响较大;而人工搜索法的强度大,危险性高,效率很低,且存在找不到落点的情况。这些都较大程度上延长了射击试验的周期,不利于试验效率的提高。
目前,弹丸落点定位方法的研究工作主要集中在被动声定位方面,且已经取得了较大的进展[1-4],定位原理是提取阵列中传感器采集到的声信号中的时间信息和阵列布阵几何中的空间信息,进行一定的换算来确定目标位置。传统的定位方式通常采用单基阵单元,特点是定向精度较高,定距误差较大,无法实现远距离条件下的定位[5-6]。而利用单基阵定向精度高的优点,使用双基阵方位线交叉定位则能够实现落点的定位[7],但是进一步的分析表明,双基阵探测存在一定盲区,无法实现全区域定位。本文以五元十字阵作为基本单元,提出了一种基于复合双基阵的弹丸落点声定位方法;对双基阵和复合双基阵模型的定位算法和定位精度进行了理论分析,并进行了外场模拟实验。精度分析表明其探测区域能够覆盖全区域;外场模拟实验结果表明基于复合双基阵的声定位方法可有效实现全区域的准确定位。
1 双基阵定位
1.1 定位原理
弹丸落地爆炸基本处于地平面,其坡度几乎为0,故忽略俯仰角,仅在平面坐标中进行研究。以五元十字阵[5]为阵型的基本单元,建立双基阵的几何模型[6],阵型分布如图1所示。

图1 双基阵模型
在Oxy坐标系内,双基阵中基阵1的中心阵元位于原点O,4个探测阵元分别位于坐标轴,离中心阵元的距离均为D,坐标分别为(0,D),(-D,0),(0,-D)和(-D,0),每个阵元布置一个性质相同的传声器;基阵2的阵列布置与基阵1相同,中心位于(r,0)。设点T(x,y)为弹丸落点,T到基阵1中心阵元O的距离为落点距离R,OT与x轴所成夹角φ1为落点方位角。爆炸声信号到达基阵中探测阵元传声器与中心传声器的时延为τ1i,距离差为d1i(i=2,3,4,5),则d1i=c×τ1i(c为声速)。双基阵和复合双基阵都是以五元十字阵作为基阵单元,单个阵列的定距、定向原理相同,故仅对单基阵的定向算法进行阐述。
根据基阵1几何关系可得:
(1)
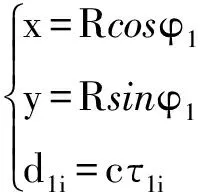
(2)
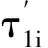
(3)
进行化简可得:
(4)
式(4)即为双基阵落点定位方程。在实际实验中,根据现场条件预先确定阵列参数,进行信号的相关处理,获取各传声器之间的时延,即可确定落点位置。
1.2 定位精度

由式(4)可知双基阵方法实现落点定位的运算量是2个基阵的方位角,受定向精度影响较大。双基阵的定向精度和单基阵是相同的,故其定向精度为[5]
(5)
分析式(5)可知,双基阵方位角误差σφ的影响因素包括有效声速c、阵列尺寸D和时延误差στ。当采样频率为5kHz时,一个采样间隔为200μs。取有效声速c=343m/s或时延估计误差στ=200μs作为精度分析的常量,阵列尺寸D为可变量,对双基阵定向精度进行分析,相对误差的分布如图2所示。
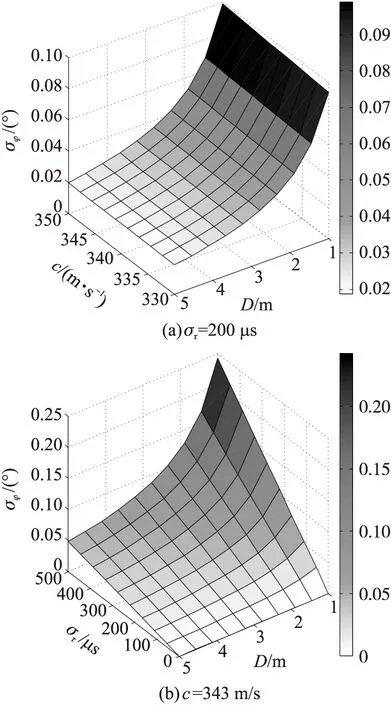
图2 方位角误差分布
从图2(a)可以得出,方位角误差σφ随有效声速c增大而增大,呈现线性关系;随阵列尺寸D的增大呈反函数减小,当D>2m时,减小趋势保持平缓,σφ基本保持在0.03°的水平。由图2(b)可知,σφ随着στ的增大同样呈线性增长;随D增大而减小,在D>2m时基本保持在0.1°的水平。
由式(4)可知,距离R同样由方位角参加计算,和方位角精度分析相似,结合误差传播理论[8]可知:
(6)
将式(4)对φ1、φ2求偏导,并将其和式(5)代入上式:
(7)
式(7)中含有复杂的三角函数,同时会有无穷大解,需要进行处理。对图1中ΔTO1O应用正弦定理:
(8)
(9)
(10)
对式(10)求偏导可得:
(11)
将式(10)代入上式化简:
(12)
式(12)即为定位距离误差的表达式,可知距离精度由有效声速c、阵列尺寸D、基阵2方位角φ2、时延估计误差στ和探测距离R等因素决定。
和方位角误差分析相同,预先设定部分参数值,即可得出在不同D、φ2、R和στ下的距离误差。图3(a)为R=100m、c=343m/s、στ=200μs时的距离误差;图3(b)为D=2m、R=100m、c=343m/s时的距离误差。
对图3(a)进行分析可知,距离误差受到方位角φ2的影响较大。当方位角φ2处于[1°,20°]及[160°,179°]的范围内,误差很大,在[1°,10°]及[170°,179°]内误差急剧增大,最小的误差达到28m,相对误差30%;在[10°,20°]及[170°,179°]范围内趋于平缓。当方位角处于[20°,160°]范围内,误差较小,总体的误差小于5%。而阵列尺寸对精度的影响相比较而言没有那么剧烈。图3(b)表明距离误差同样受到方位角φ2的影响较大,受到时延估计误差的影响较小,且分布规律和图3(a)类似。
阵列间距r是与时间t无关的参量,则r对定距精度σR的影响为
(13)
对式(10)求偏导可得:
(14)
将式(9)代入上式:
(15)
由几何关系可知:
(16)
代入式(15)并进行化简可得:
(17)
式(17)即为阵列间距r对定距精度的影响表达式,可知精度受到R和r的共同作用,相对定距误差为1/r,即理论上r确定后相对定距误差恒定。当r ≥15m时,相对定距误差小于6.67%,误差在可接受范围之内。在测试条件允许的前提下,应该尽量增大阵列间距。
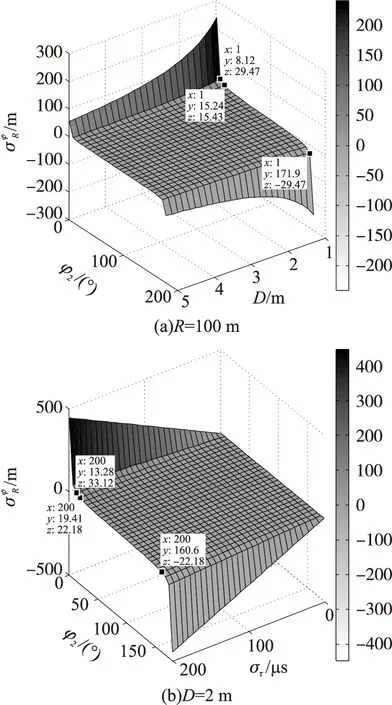
图3 距离误差分布
图4为距离误差分布图。由图4可知,当阵列间距r=10m时,最大距离误差在距离R=100m时约为10m,相对误差为10%;而在r=15m时,相对的距离误差小于7%。
对双基阵定位方法的精度分析表明:双基阵在大部分定位区域的精度较高,但是在参考方向(x轴)附近有一定大小的区域较低(距离误差>10%),无法在整个靶场区域内实现弹丸的落点定位。由上述分析可知,双基阵定位的探测盲区关于x轴对称,其范围如图5所示。
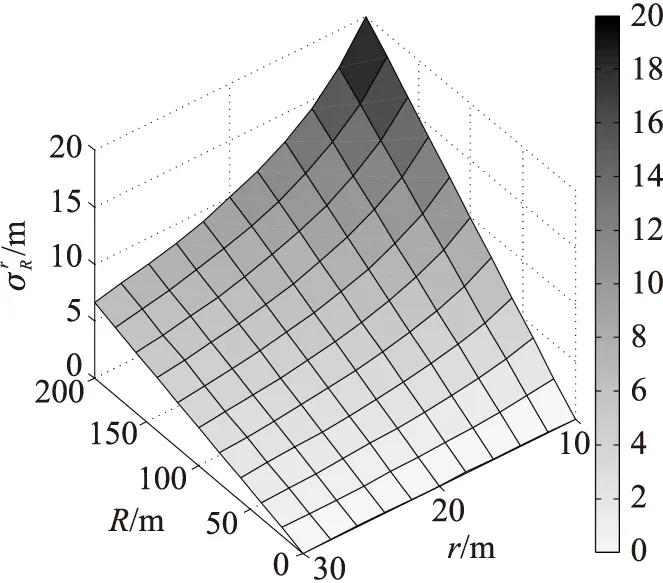
图4 距离误差分布
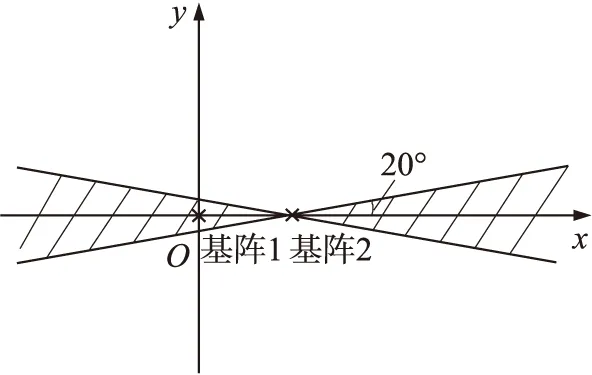
图5 双基阵定位探测盲区
由图5可知,探测区域中存在以基阵2为中心的扇形探测盲区,圆心角为80°,占整个区域的2/9。当落点距离R=100m时,盲区面积约为6 981m2,覆盖范围较大,无法满足定位要求。
2 复合双基阵定位
2.1 定位原理
双基阵探测盲区是以基阵2为中心的辐射扇形区域,在其基础上添加一个基阵3,垂直于x轴,并共用基阵2的信息形成另一个双基阵定位系统,使其有效探测区域覆盖基阵1、基阵2定位的探测盲区,确保全区域定位的实现。
复合双基阵模型如图6所示。基阵1、基阵2与双基阵模型相同,基阵3中心传声坐标为O2(r,r),连线O2T与水平方向夹角为φ3。复合阵定位系统中,基阵1、基阵2形成主双基阵定位系统,同时基阵1、基阵3形成辅助双基阵定位系统。
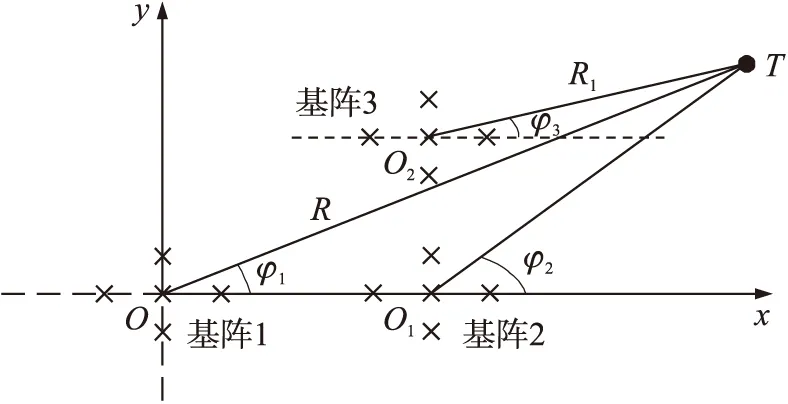
图6 复合双基阵模型
复合双基阵定位是由2个双基阵进行的复合定位,需要对辅助双基阵定位算法进行推导。设目标信号到达基阵3时延为τ″1i,距离差为d″1i,则有d″1i=c×τ″1i。由式(2)、式(4)可得基阵3定位表达式为
(18)
当落点处于主双基阵的探测盲区中时,无法准确定位,则使用辅助双基阵进行定位。依据式(2)得出落点的方位角φ1。同时,依据式(6)可得出从基阵3中心传感器出发的落点方位角φ3和距离R1,然后根据基阵间的几何关系进行换算,最终确定出落点位置。
综合上述可得出弹丸落点的坐标公式为
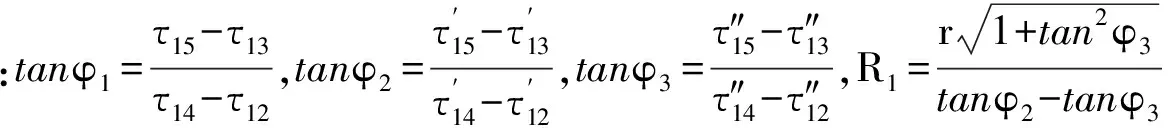
2.2 定位精度
复合双基阵是由2个双基阵定位系统组成,其精度分析过程基本相似。改进阵型的出发点是提高定距精度,故将2种阵列形式的定距误差进行综合对比。设定即时声速c=343m/s,阵列尺寸D=3m,时延估计误差στ=100μs,对定距精度进行分析,相对误差分布如图7所示。
由图7可知,相同条件下双基阵的距离误差随基阵2方位角φ2的增大而减小,最大距离误差σR,max=150m,当φ2<10°时,随其增加而急剧下降;当φ2>20°时基本保持在10m的水平,误差较小。复合双基阵的误差曲线由2个部分组成,但在整体范围内距离误差小于10m,即最大相对距离误差σR,max=1%。
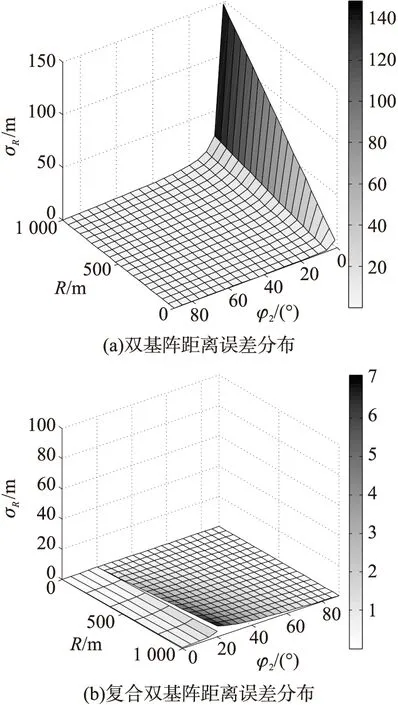
图7 2种定位方式距离误差对比
综上所述,复合双基阵能有效克服双基阵存在探测盲区的缺陷,实现全区域定位;在情况允许的前提下,应尽量满足阵列尺寸D>3 m以及时延估计误差στ<100 μs的条件。
3 实验结果分析
3.1 实验过程简述
参考靶场环境,进行了外场模拟定位实验。按图6布置复合双基阵,参考前文的精度分析结果,设定阵列尺寸D=3 m,阵列间距r=15 m,使用少量炸药爆炸产生模拟声波,炸点位置示意图如图8所示,每个实验点重复进行3次,取3次实验结果的算数平均值作为最终定位结果。
图9为基阵1采集到的爆炸声信号(A为信号幅度,t为采样时间),此信号为典型的脉冲信号,在信号到达传感器之前基本保持零值,到达后幅值迅速变化,并很快衰减至0,特征十分明显,信号相关性较好。

图8 炸点位置示意图
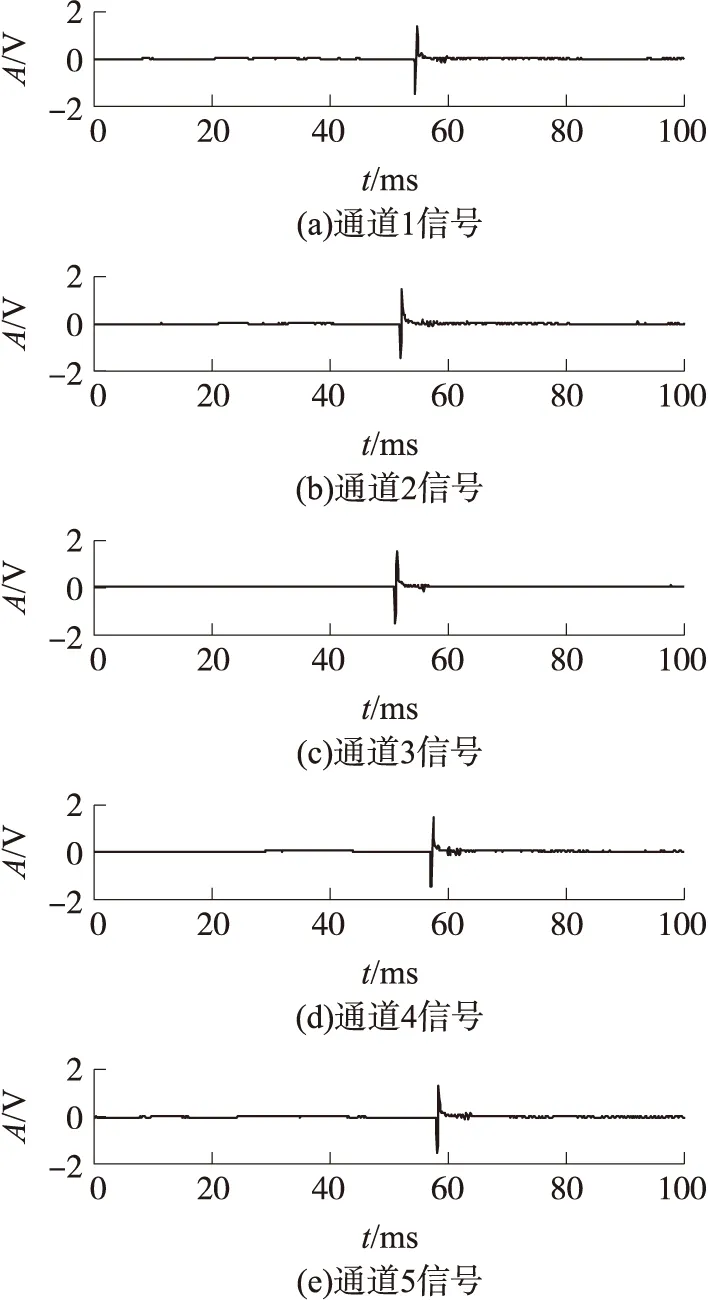
图9 实测声信号时域图
3.2 定位结果分析
对实验数据进行相关处理,获取每个基阵中传声器的时延,并根据定位公式计算模拟声源坐标,对每个测试点进行的3次结果取算数平均,作为最终定位结果。为便于叙述,把实验中的炸点位置称为预设值,定位结果称为实验值,进行处理后汇总如表1所列。
在定位实验中,测试点7、测试点8处于主双基阵的探测盲区,定位结果:测点7为(23.10,1.3),R=23.14 m,相对误差ε=15.70%;测点8为(27.86,-2.5),R=27.97 m,ε=6.77%,误差较大。经辅助双基阵运算后对实验数据进行替代,可得表1中数据。
对表1中数据进行分析可知,复合双基阵定位较为准确,定向精度较高,最大相对方位角误差约为1%,最小为0.02%;而定距精度相对差一些,最大相对距离误差为3.17%,最小为0.13%。说明复合双基阵的定位能力较好。
实验定位结果的散布如图10所示,误差分布如图11所示。图中S为测点序号。
由图10能够较为明显地看出,定位结果基本上分布在预设实验点的周围,散布较小,基本在4 m以内的散布圆之内。1号和2号实验点误差较大,分析其原因可能是传播过程中信号受到了自然风的影响,最大误差达到了接近5 m,但是8个实验点总体上定位精度较高。
图11的相对误差分布表明,复合双基阵定位的定向误差很小,部分达到了理论分析精度,最大误差约在1%的水平;而距离精度要相对低一些,双基阵的定位误差最大是7号实验点,达到了16%,8号次之,误差也达到了7%,不能满足定位的要求。而经过复合双基阵定位改进后,精度得到了提高,总体距离误差小于4%。
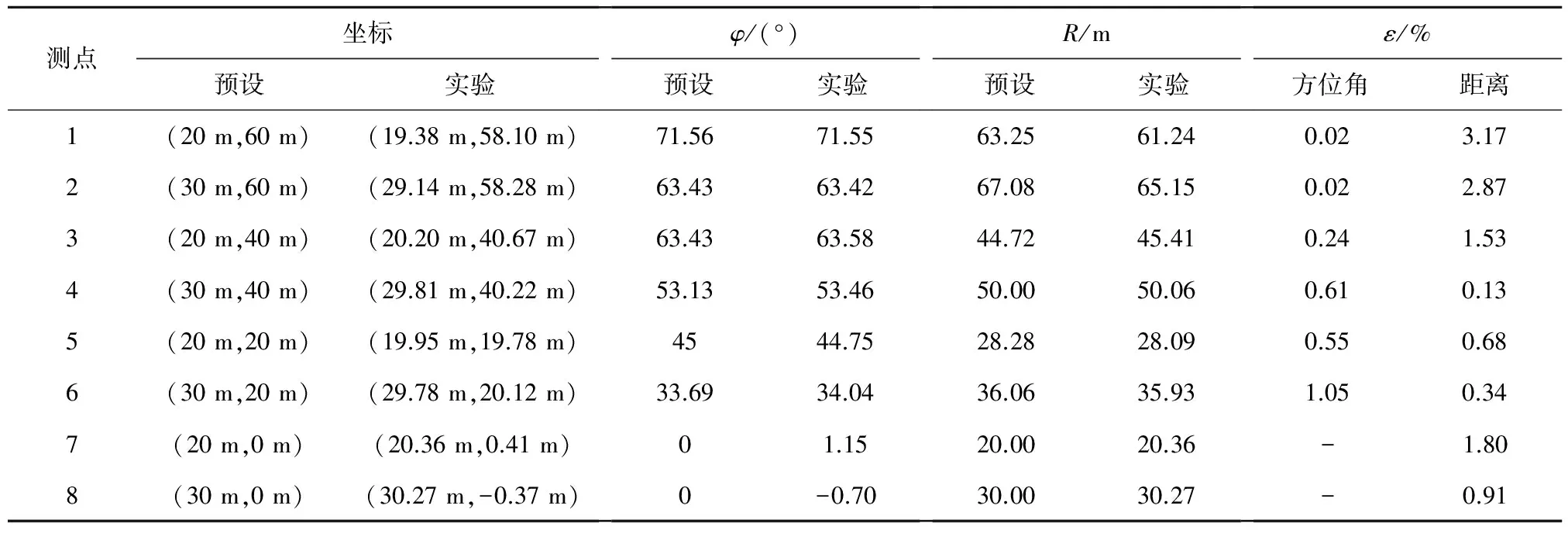
表1 声定位结果
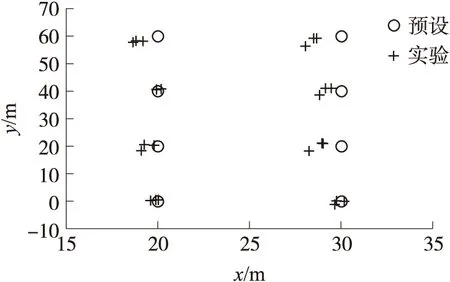
图10 实验结果散布示意图
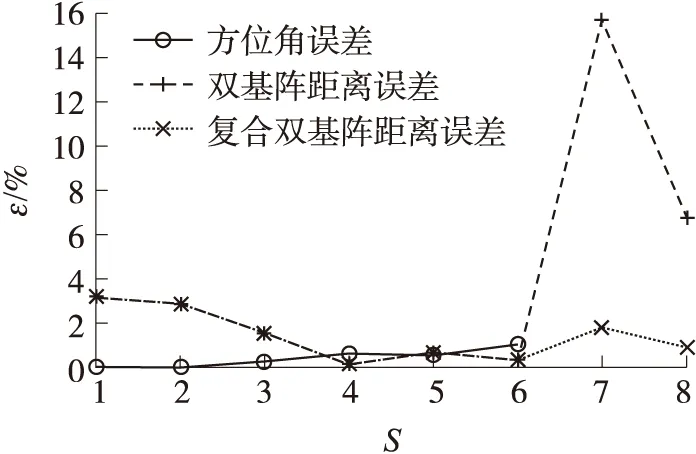
图11 实验结果误差分布
4 结束语
以五元十字阵为组成阵型的基本单元,对双基阵方法的定位算法和定位精度进行了理论仿真分析,针对双基阵方法在参考方向区域存在一定范围探测盲区的缺陷,提出了一种基于复合双基阵的弹丸落点声定位方法,对其进行了理论分析和实验验证。实验结果表明:复合双基阵落点定位观测方法的相对方位角误差和距离误差均小于4%,定位精度较高,解决了双基阵存在探测盲区的问题。由于条件和场地受限,本文进行的是室外的模拟声定位实验,探测距离也并不是很远,在远场以及靶场 射击试验中的应用还需要进一步的研究。
[1] 杨亦春,滕鹏晓,李晓东,等.小孔径方阵对大气中运动声源的定位研究[J].声学学报,2004,29(4):346-352.
YANG Yi-chun,TENG Peng-xiao,LI Xiao-dong,et al.Study of acoustic position for moving sources in low sky with a small spatial array[J].Acta Acustica,2004,29(4):346-352.(in Chinese)
[2]冯斌,石秀华.双三角阵声靶测试系统研究[J].应用声学,2012,31(2):140-144. FENG Bin,SHI Xiu-hua.Studies of acoustic target with two equilateral triangle arrays[J].Applied Acoustics,2012,31(2):140-144.(in Chinese)
[3]程翔,张河.基于纯测角的直升机飞行轨迹与拦截角估计[J].弹箭与制导学报,2007,27(2):173-176. CHENG Xiang,ZHANG He.Estimation of flight track and head off angle of helicopter based on angle-only measurement[J].Journal of Projectiles,Rockets and Missiles,2007,27(2):173-176.(in Chinese)
[4]罗晓松,冯杰,柳华林,等.基于声震探测技术的靶场炸点坐标测量误差分析[J].飞行器测控学报,2014,34(2):176-182. LUO Xiao-song,FENG Jie,LIU Hua-lin,et al.A seismic-acoustic detection method for determination of the coordinates of projectile impact points at shooting ranges and error analysis[J].Journal of Spacecraft TT&C Technology,2014,34(2):176-182.(in Chinese)
[5]陈华伟,赵俊渭,郭业才.五元十字阵被动声定位算法及其性能研究[J].探测与控制学报,2003,25(4):11-16. CHEN Hua-wei,ZHAO Jun-wei,GUO Ye-cai.Acoustic passive localization algorithm based on a planar five-element array and its performance analysis[J].Journal of Detection & Control,2003,25(4):11-16.(in Chinese)
[6]刘新爱,狄长安,孔德仁.基于菱形阵列的弹丸落点定位模型研究[J].火炮发射与控制学报,2012(4):91-96. LIU Xin-ai,DI Chang-an,KONG De-ren.Study on projectile impact point positioning model based on diamond-shaped array[J].Journal of Gun Launch & Control,2012(4):91-96.(in Chinese)
[7]张炳文,郑坚,熊超,等.弹丸落点双基阵声学定位技术研究[J].弹箭与制导学报,2013,33(1):100-103. ZHANG Bing-wen,ZHENG Jian,XIONG Chao,et al.Acoustic locating method of impact points based on double-array[J].Journal of Projectiles,Rockets,Missiles and Guidance,2013,33(1):100-103.(in Chinese)
[8]肖明耀.误差理论及应用[M].北京:计量出版社,1985. XIAO Ming-yao.Error theory and application[M].Beijing:Metrology Press,1985.(in Chinese)
Acoustic Location Method of Projectile Impact-point Based on Compound Double-Arrays
ZHENG Jian,ZHANG Bing-wen,XIONG Chao
(Department of Artillery Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
By the acoustic location method based on the single array,the obtained distance error of projectile impact-point is large,but the direction error is small.Aiming at this problem,the location of projectile impact-point was achieved by crossing the azimuth lines of two arrays.Aiming at the blind area of double arrays method,an acoustic location method based on compound double arrays was put forward.Taking five-elements cross arrays as the basic units of compound arrays,the mathematical models of double arrays and compound double arrays were established,and the analysis on locating algorithm and locating precision of methods was conducted.The result of out-field experiment shows that the whole area acoustic location of projectile impact-points can be achieved by method of compound double arrays,and the relative azimuth error and distance error are less than 4%,and the location precision is high.
projectile;impact point;location;five-elements cross array;acoustic;compound double arrays
2016-07-12
郑坚(1962- ),男,教授,博士,研究方向为阵列信号处理技术。E-mail:zhengjian62@sohu.com。
TJ011.1
A
1004-499X(2016)04-0068-07

