连续射击下的枪管瞬态传热模型

冯国铜,周克栋,赫 雷,王靖亚,张英琦,李峻松

(1.南京理工大学 机械工程学院,南京 210094;2.中国兵器工业第二〇八研究所,北京 102202)



连续射击下的枪管瞬态传热模型

冯国铜1,周克栋1,赫 雷1,王靖亚1,张英琦1,李峻松2

(1.南京理工大学 机械工程学院,南京 210094;2.中国兵器工业第二〇八研究所,北京 102202)

针对连续射击过程中周期性瞬态热冲击引发的身管烧蚀问题,建立了身管一维瞬态传热的数学模型。采用能量平衡法,应用交替隐式差分格式(ADI),推导了内节点及边界点的有限差分方程,以经典内弹道数值计算结果为基础,通过VB编程求解了连续射击120发弹过程中某12.7 mm机枪枪管的温度场分布。采用红外热像仪对身管外壁温度进行了测试,数值仿真结果相对于实验结果的误差小于10%,所建模型及采用的算法是有效的。研究得到的枪管温度场的变化规律为更加深入地研究身管烧蚀机理、设计身管结构以及预测身管寿命提供了可靠的理论依据。

机枪;身管温度;身管烧蚀;瞬态热传导;数值仿真

枪管内膛烧蚀是热、化学、机械综合作用的结果,其中热起主导作用[1-3]。热量在身管内的传递属于三维非稳态传热过程,两维或三维传热模型应用在枪管传热问题上则更为准确,但应用两维或三维传热模型所编制的程序时每次计算所需时间较长。而对于某些枪管而言,需多次且快速地预测不同材料、不同结构、不同环境温度及不同射击规范下的枪管温度场,为枪管其他性能的研究及时提供热载荷,其计算量极大[4]。以此为背景,本文建立了一维瞬态热传导模型,编程计算了枪管温度随时间和空间的变化规律。

1 身管径向一维传热模型

1.1 模型假定

①由于枪管径向温度梯度的量级比轴向及周向温度梯度量级大得多,因此,忽略枪管轴向及周向的温度梯度,仅考虑径向温度梯度[4]。

②假定每一发弹的内弹道参数各自独立且完全相同。

③忽略弹丸与身管摩擦产生的热量。

④忽略身管材料的热膨胀(密度为常数),假定导热系数、热容量均为常数。

⑤忽略枪管向枪械其他部件的传热。

1.2 控制方程

(1)

式中:T为枪管壁的温度,t为时间,r为枪管壁中某点距身管对称轴的距离,a为枪管材料的导温系数。

1.3 定解条件

①初始条件。

首发射击时,T=Ta,Ta为环境温度。

连发射击时,T=f(r),f(r)为已射击弹药引起的身管径向温度分布。

②内外边界条件。

内边界条件为

外边界条件为

式中:λ为身管材料的导热系数;r0,rN分别为身管内、外半径;Tg,Ta分别为膛内火药气体温度与周围环境温度;hg为火药气体与枪管内表面的导热系数;ha为周围环境与枪管外表面的导热系数。

1.4 复合换热系数求解

1)火药气体对身管内壁的对流换热系数的确定。

①在内弹道和后效期时期,火药气体在膛内的流动属于管内强迫对流换热与辐射换热。

对流换热系数为

(2)

式中:vg为火药气体的速度,ρg为火药气体的密度,d为枪管口径,λg为火药气体的导热系数,cp为火药气体的比定压热容,μg为火药气体的动力粘度。

辐射换热系数为

(3)

复合换热系数为h1=hg1+he1,需在枪管温度场模型分析中迭代求解。

②在后效期结束的瞬间,管内火药气体排空,管内为空气,温度为室温。在空冷期,管内属于自然对流,其对流换热系数为

(4)

式中:νa为空气的运动粘度,aa为空气的导温系数,λa为空气的导热系数。

2)身管外壁对周围环境的复合换热系数的确定。

在内弹道、后效期与空冷期这3个时期,身管外壁与周围环境之间均属于自然对流换热与辐射换热。

对流换热系数为

(5)

式中:dN为枪管外径。

辐射换热系数为

(6)

式中:εa为空气的辐射率。

复合换热系数为

h2=h′+he

2 身管传热数值分析

2.1 控制方程的离散

以管壁内部任意点作为考虑的内点,如图1所示。图中,Δθ为枪管壁周向微元,i为枪管壁径向节点的序数。

考虑图中阴影部分的控制容积的能量守恒,采用无条件稳定的交替隐式(ADI)差分格式可得[5]:

(7)

整理得:

(8)

式中:

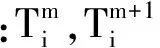
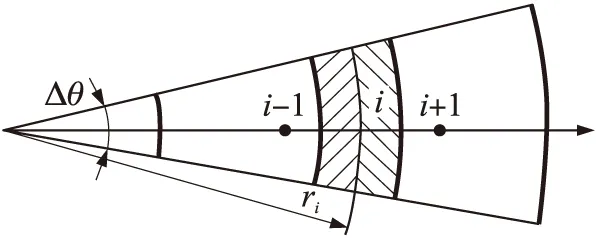
图1 内点示意图

2.2 边界条件的离散

边界节点亦采用能量平衡法,容易推得内、外边界条件的离散格式的隐式格式:

(9)

式中:

3 仿真与试验验证

本文计算了环境温度为0 ℃时某12.7 mm机枪枪管的温度场,所计算的射击状态为120连发,所采取的射击规范为“60发—空冷3 min—60发—空冷3 min”,按照国军标要求,其中,每组60发弹又分为3个短点射和2个长点射。

为了验证上述分析模型及数值仿真结果的正确性,本文对该12.7 mm机枪进行了测试研究。

以往测量枪管温度场的方法是在枪管上加工盲孔,用热电偶测量枪管壁某一径向位置的温度,该位置由盲孔的深度决定[6-7]。然而在枪管上加工盲孔会引起枪管温度场在盲孔周围发生温度畸变,使测量值与真实值之间的误差较大[8-9]。

本试验采用红外热像仪[10]对该12.7 mm机枪连续射击120发时的身管外表面温度进行了测试,测试时长涵盖了外表面的温度上升期与冷却期。测试时环境温度为0 ℃。图2为射击过程某时刻该12.7mm机枪身管外表面的温度分布云图。表1为该12.7 mm机枪枪管轴向距枪管口部不同距离处枪管外表面若干特殊时刻的温度测试值。表中,x为所取截面距枪口的距离。

图2 射击时身管某时刻外表面温度分布云图

截面x/mmTN/℃60发后空冷3min后120发后空冷3min后A70347．2238．6480．6334．5B140382．2278510．7368．9C210379．6291．1514．5386．4D280372．0282．8507．3385．2E350334．4239．2458．1344．3F400284．7228．8422．4341．5G480293．5248．6437．3359．8H560293．5242．6431．2356．2I620290．9240．8429．8354．8J720288．8247．7436．5359．6K820275．4202．3396．2299．8

由表1可知,在整个120发过程中,外表面温度最高的截面为C截面。不失一般性,本文选取温度最高的C截面以及J截面为对比截面,对比结果见图3、图4以及表2。表中,TN,S为枪管外表面温度仿真值,TN,T为枪管外表面温度试验值,ΔTN为相对误差。

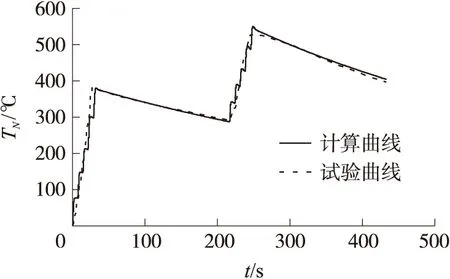
图3 枪管C截面外表面TN-t曲线

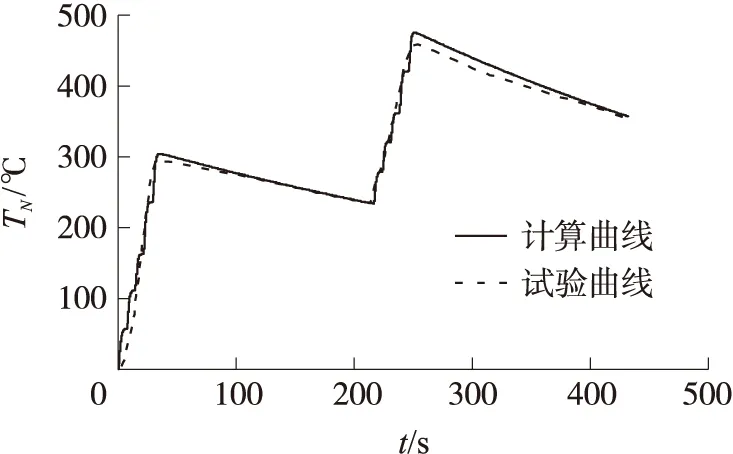
图4 枪管J截面外表面TN-t曲线

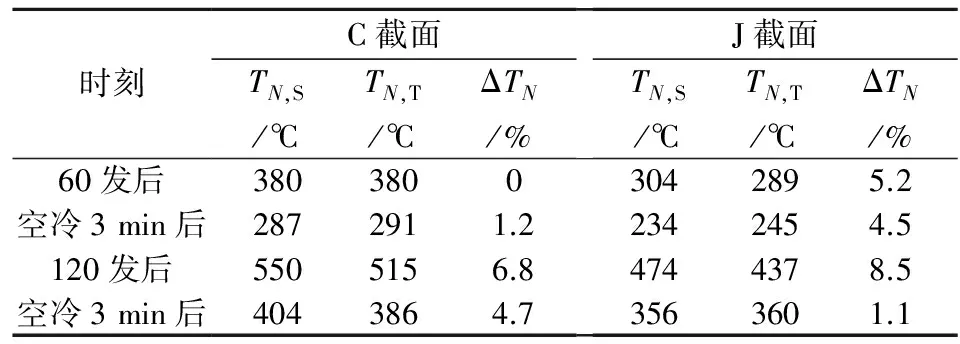
时刻C截面TN，S/℃TN，T/℃ΔTN/%J截面TN，S/℃TN，T/℃ΔTN/%60发后38038003042895．2空冷3min后2872911．22342454．5120发后5505156．84744378．5空冷3min后4043864．73563601．1

由表2可见,计算所得枪管外表面温度与试验所得温度误差很小,相对误差均小于10%,本文所建立的模型准确可靠。

4 仿真结果与分析

4.1 单发射击时枪管温度场仿真与分析

进行单发射击的枪管温度场仿真与分析是为连发射击时枪管温度场仿真打下基础。

由于C截面为射击过程中枪管壁温度最高的截面,故以下分析皆以C截面为参考截面。图5为C截面处枪管壁不同径向位置T-t曲线。从身管内壁温度-时间曲线(r=6.35 mm处)可知,内弹道时期,火药气体流速剧增,雷诺数也随之增大,膛内气流为湍流流动,火药燃气迅速向壁面传热,壁面温度急剧上升到峰值292 ℃。在后效期,火药气体逐渐排出枪管,膛压衰减,膛内气流温度也下降,并伴随着身管壁内部热传导,导致壁面温度逐渐下降。

对比不同径向位置T-t曲线,靠近壁面的节点温度经历先增后减的过程,离内壁面较远的节点温度较为平缓,呈稳定上升趋势。

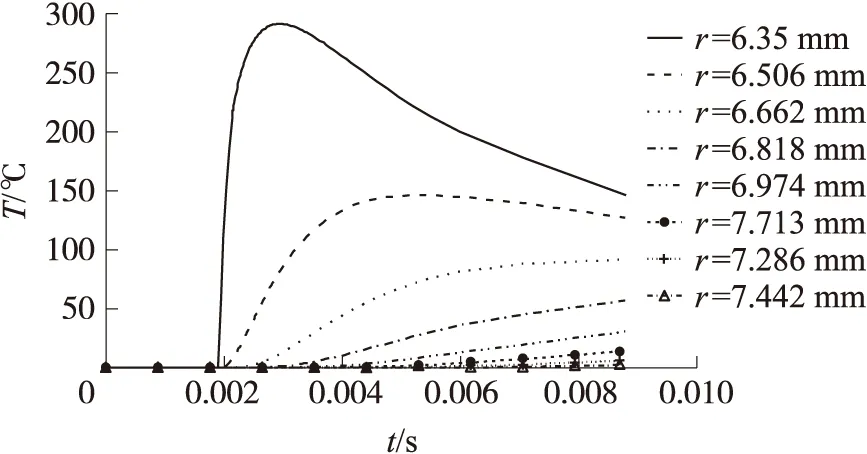
图5 C截面处枪管壁不同径向位置T-t曲线

图6为C截面处枪管壁不同时刻的T-r曲线。单发射击时间很短,由膛内火药燃气传递给身管的热量很有限,并且该热量来不及扩散,因此在径向传播的厚度大概为1.1 mm,只有靠近内壁面的节点存在较大温度梯度,外壁温度几乎没有变化,这就是单发射击时可以将身管模型简化为半无限大平板的原因[8]。

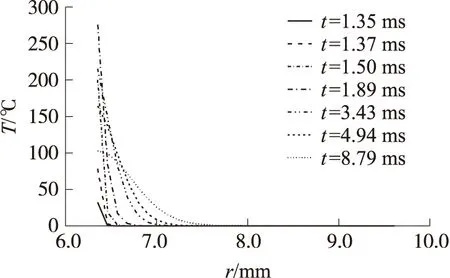
图6 C截面处不同时刻身管壁T-r曲线

4.2 连发射击时枪管温度场仿真与分析

图7～图10为连发射击时枪管壁温度分布曲线。图7、图8分别为第1组、第2组60发弹过程中参考截面处枪管壁不同径向位置的T-t曲线,其中第1、第2、第3个点射均为10发点射,第4、第5个点射均为15发点射。由于“空冷3 min”所用的时间相对于连续射击60发而言较长,图中仅给出部分冷却时段(即不足3 min)的T-t曲线,省略的部分各曲线沿图中趋势无限靠近、趋于重合。

图7 第1组60发弹枪管壁温度随时间的变化规律

由图8可知,射击120发弹后,枪管内表面温度最高可达827 ℃,但此温度会在10 ms内衰减到594 ℃,而后缓慢衰减。

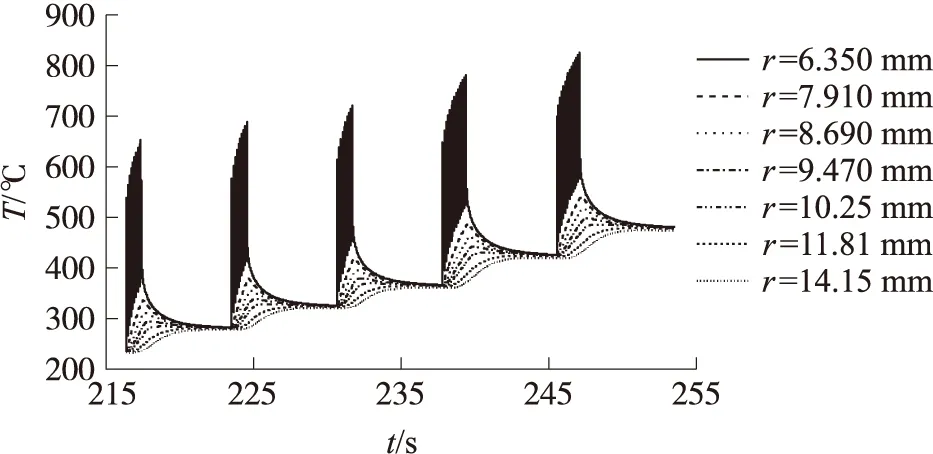
图8 第2组60发弹枪管壁温度随时间的变化规律

由图7、图8可得,内弹道与后效期时,越靠近枪管内表面,枪管温度越高且波动越大,由于枪管内表面与火药气体直接接触,其温度值有非常明显的脉冲波动。在空冷期,枪管壁径向温度梯度较小且越来越小。越靠近外表面,枪管壁达到温度最高点的时间越滞后。

图9为不同弹序参考截面处枪管壁的T-r曲线,所选时间点为每发弹“内弹道—后效期—空冷期”一个周期结束时刻。可见,随着射弹数的增加,枪管内壁温度均有明显增加,但每发弹所增加的温度梯度逐渐减小,且随着时间的推移,热量由枪管内壁向外壁逐层传导,在第4发弹之后,枪管外壁温度有明显增加的趋势。

图10为射击120发弹后身管壁冷却过程中的T-r曲线,可见,射击结束后身管内壁温度即刻下降,但由于热传导,身管外壁温度继续升高,在持续10 s后,身管径向温度梯度几乎消失,内外壁温度以近似同一速率衰减。

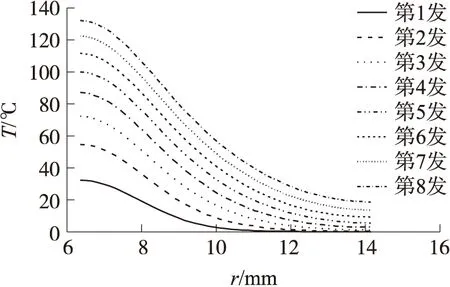
图9 不同弹序身管壁T-r曲线

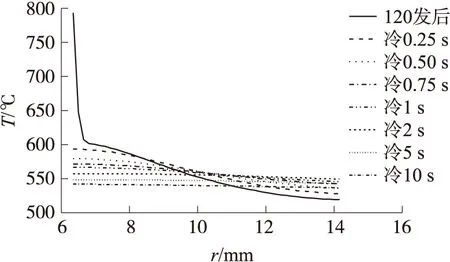
图10 射击120发弹后身管壁冷却过程中的T-r曲线

5 结束语

本文对枪管连续射击过程中的导热问题进行了深入的分析研究,得出以下结论:

①单发射击时,枪管内表面温度最高可达292 ℃。膛内火药燃气在径向传播的厚度大约为1.1 mm,靠近内壁面的节点存在较大温度梯度,外壁温度几乎没有变化,因此单发射击时可以将身管模型简化为半无限大平板。

②连发射击时,射击120发弹后,枪管内表面温度最高可达827 ℃,但此温度会在10 ms内衰减到594 ℃,而后缓慢衰减。

③随着射弹数的增加,枪管内壁温度明显增加,但每发弹所增加的温度值逐渐减小,且随着时间的推移,热量由枪管内壁向外壁逐层传导,在第4发弹之后,枪管外壁温度有明显增加的趋势。

④射击结束后身管内壁温度即刻下降,但由于热传导,身管外壁温度继续升高,在持续10 s后,身管径向温度梯度几乎消失,内外壁温度以近似同一速率衰减。

本文建立了枪管温度场理论分析模型,对枪管在连续射击下的导热问题进行了深入的研究,得到枪管温度场变化规律。研究结果具有很高的科研及工程价值。

[1] JOHNSTON I A.Understanding and predicting gun barrel erosion,ADA440938[R].2005.

[2]SOPOK S,RICKARD C,DUNN S.Thermal chemical mechanical gun bore erosion of advanced artillery part two:modeling and prediction[J].Wear,2005,258:671-683.

[3]LAWTON B.Thermo-chemical erosion in gun barrels[J].Wear,2001,251:827-838.

[4]HILL R D,CONNER J M.Transient heat transfer model of machine gun barrels[J].Materials and Manufacturing Processes,2012,27(8):840-845.

[5]周克栋,陆家鹏,高星亮.速射武器身管一维径向传热的数值分析[J].弹道学报,1993,5(1):27-31. ZHOU Ke-dong,LU Jia-peng,GAO Xing-liang.Numerical analysis of one-dimensional radial heat transfer for rapidly firing gun barrel[J].Journal of Ballistics,1993,5(1):27-31.(in Chinese)

[6] HAMEED A,AZAVEDO M,PITCHER P.Experimental investigation of a cook-off temperature in a hot barrel[J].Defence Technology,2014,10:86-91.

[7] 李杰,余永刚,周彦煌.枪(炮)膛内温度间接测量方法研究[J].弹道学报,2005,17(3):36-39. LI Jie,YU Yong-gang,ZHOU Yan-huang.Study of an indirect method measuring inside-wall temperature of gun tube[J].Journal of Ballistics,2005,17(3):36-39.(in Chinese)

[8]毋笃强.膛面温度和热流的外推方法及温度场计算[J].南京理工大学学报,1985,34:201-218. WU Du-qiang.The extrapolation method of temperature and heat flow on the chamber surface and the computation of temperature field[J].Journal of Nanjing University of Science and Technology,1985,34:201-218.(in Chinese)

[9]黄凤良,夏春梅,周彦煌,等.温度测试的外推方法[J].计量学报,2003,24(2):116-118. HUANG Feng-liang,XIA Chun-mei,ZHOU Yan-huang,et al.Extrapolation method for the measurement of temperature[J].Acta Metrologica Sinica,2003,24(2):116-118.(in Chinese)

[10]李云红.基于红外热像仪的温度测量技术及其应用研究[D].哈尔滨:哈尔滨工业大学,2010. LI Yun-hong.Research on temperature measurement technology and application based on infrared thermal imager[D].Harbin:Harbin Institute of Technology,2010.(in Chinese)

[11]WU Bin,CHEN Gang,XIA Wei.Heat transfer in a 155 mm compound gun barrel with full length integral midwall cooling channels[J].Applied Thermal Engineering,2008,28:881-888.

[12]CHUNG Dong-yoon,SHIN N.Prediction of erosion from heat transfer measurements of 40 mm gun tubes[J].Wear,2007,263:246-250.

[13]GERTER N,BUNDY M L.Heating of a tank gun barrel-numerical study,ADA241136[R].1991.

[14]STEINHEIMER R,ENGEL B.Thermal influences during rotary draw bending of tubes from stainless steel[J].Procedia Engineering,2014,81:2165-2170.

[15]CARTER E A.First principles and multiscale modeling of spallation and erosion of gun tubes,ADA459432[R].2005.

[16]吴斌,夏伟,汤勇,等.大口径火炮身管主动冷却温度场分析[J].兵工学报,2004,25(3):267-271. WU Bin,XIA Wei,TANG Yong,et al.Temperature field analysis for actively cooled barrel of large caliber gun[J].Acta Armamentarii,2004,25(3):267-271.(in Chinese)

Transient Heat Transfer Model of Gun Barrel Under Successive Firing

FENG Guo-tong1,ZHOU Ke-dong1,HE-Lei1,WANG Jing-ya1,ZHANG Ying-qi1,LI Jun-song2

(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China; 2.No.208 Research Institute of China Ordnance Industries,Beijing 102202,China)

Aiming at gun erosion caused by periodic transient-thermal-shock during succession firing,the mathematical model of one-dimensional transient-heat-transfer of gun barrel was established.The finite difference equations of internal nodes and boundary nodes were derived by using energy balance method and ADI(Alternating Difference Implicit)scheme.Based on the numerical results of the classical interior ballistics,the temperature distribution of barrel of some 12.7 mm machine gun during 120 succession firing rounds was calculated numerically by Visual Basic programming.The temperature test was conducted by thermal infrared imager.The error of the numerical result relative to the experimental result is less than 10%,and the established model and the used algorithm are effective.The obtained change law of barrel temperature-field has great importance for the further studies of gun barrel erosion mechanism,and the result provides the reliable theory basis for the structure design and the life prediction of gun barrel.

machine gun;gun barrel temperature;gun barrel erosion;transient heat transfer;numerical simulation

2016-07-10

中国人民解放军总装备部瓶颈项目

冯国铜(1989- ),男,博士研究生,研究方向为轻武器理论、仿真及试验,传质传热学,结构动力学。E-mail:fengguotong1989@163.com。

TK513.5

A

1004-499X(2016)04-0075-05