基于hp自适应伪谱法的变后掠翼导弹弹道优化设计

王 娜,陈洁卿,明 超,孙瑞胜

(南京理工大学 能源与动力工程学院,南京 210094)



基于hp自适应伪谱法的变后掠翼导弹弹道优化设计

王 娜,陈洁卿,明 超,孙瑞胜

(南京理工大学 能源与动力工程学院,南京 210094)

为了提高变后掠翼导弹的终端速度,对其末端弹道优化问题进行了研究。基于终端速度最大,采用后掠角和攻角双变量优化方案,建立了在动压、过载及边界条件等多约束条件下的弹道优化模型。鉴于全局伪谱法在解决复杂多约束条件下最优控制问题存在的局限性,采用将全局伪谱法与hp型有限元法融合的hp自适应伪谱法,将弹道优化问题转化为非线性规划问题,并将仿真结果与已有的粒子群算法的最优弹道对比,验证了模型和方法的正确性。结果表明,采用hp自适应伪谱法得到的最优弹道在保证了较高的命中精度的前提下,能够以更高的终端速度和更佳的弹体姿态攻击目标。

变后掠翼导弹;终端速度;hp自适应伪谱法;弹道优化

变后掠导弹在飞行过程中通过主动改变后掠角,实时改变弹翼翼面形状或剖面形状,使得导弹在不同弹道阶段、各个速度包络内都具有良好的飞行力学性能,较固定翼导弹有许多优点[1-2],其射程远、突防能力强、毁伤效果好,提高了打击机动目标的能力[3～4]。但是,后掠角的变化过程使得导弹的飞行力学设计和弹道特性变得更为复杂,这使得变后掠翼导弹的弹道优化设计较固定翼更为复杂,其核心是寻找适合变后掠翼导弹的弹道优化设计方法。

目前在弹道优化方面常用的优化方法有直接法和间接法两大类[5]。但是间接法对初值很敏感,收敛半径小,求解很困难[5]。因此,借助优化理论,直接通过迭代寻优求解最优轨迹的直接法获得了研究者的重视。

直接法主要包括打靶法、配点法、粒子群算法(PSO)等[5]。其中,打靶法只离散控制变量,且能够用较少的优化参数获得高精度的解。文献[6]利用打靶法将控制变量攻角α在空域上参数化,将弹道优化问题转化为参数优化问题。但当离散点数目增加时,非线性规划(NLP)规模急剧增大,运算量过大,需要很长时间才能求得满足要求的解[7-8]。同时,目前难以证明所得的解收敛于系统最优控制。粒子群算法是一种基于群智能方法的进化算法,容易实现,具有全局收敛性。文献[9～11]采用将最优控制与粒子群算法相结合的原理,研究了变后掠翼导弹的增程能力与投放条件之间的关系。但是粒子群算法也和其他全局优化算法一样,容易陷入局部最优,收敛精度不高,后期收敛速度慢[7]。配点法同时离散控制变量和状态变量,包括伪谱法(PM)、Hermit-Simpson法、Runge-Kutta法以及欧拉法,其中PM是配点法中最为活跃的分支。根据离散点选取方法的不同,常见的PM又分为Gauss伪谱法(GPM)、Legendre伪谱法(LPM)和Radau伪谱法(RPM)[12-13]。其中RPM以其指数性的收敛速度、简单的结构以及很高的收敛精度受到了广泛的重视,为变后掠翼导弹弹道优化提出了新思路。文献[14～15]利用RPM求解满足路径约束和终端约束条件下的射程最远弹道轨迹,选取后掠角和攻角作为优化控制变量,并通过采取一系列实时性保证策略提高算法的计算效率,实现变后掠导弹弹道的在线重构。虽然对于简单、约束较少的弹道优化问题,RPM能够快速求得理想解,但是对于复杂、多约束的最优控制问题,RPM需要用较高维的插值多项式才能得到近似解,而hp自适应伪谱法(hp-RPM)能够对不满足精度要求的区间宽度h和全局插值多项式的阶次p进行自适应调整,用较少的计算代价得到较高精度的解。

另外,现代武器的发展要求变后掠翼导弹除了能够以较高的精度命中目标外,还要尽可能提高变后掠导弹终端速度,加强导弹的攻击能力。为此本文以终端速度最大为性能指标,在动压、过载及边界条件等多约束条件下,采用hp自适应伪谱法对变后掠导弹的末端弹道进行优化设计,并与已有的粒子群算法的最优弹道进行对比,验证模型及方法的正确性,为变后掠导弹总体设计提供理论指导和技术参考。

1 问题描述

用数学语言描述变后掠翼导弹弹道优化问题实际上是一组包含微分-代数约束和不等式约束的非线性最优控制问题,即在满足各种约束的条件下,寻找符合条件的控制方程,使得导弹的终端速度最大。

1.1 动力学模型

基于“瞬时平衡”假设,把变后掠翼导弹看成一个可操控的质点,只研究导弹质心在纵向平面内的运动。

(1)

式中:m为导弹质量;g为重力加速度;x,y分别为射程和射高;v为导弹速度;θ为弹道倾角;阻力Fx=qSCx,升力Fy=qSCy,S为参考面积,动压q=ρv2/2,Cx,Cy分别为阻力和升力的气动力系数,是马赫数Ma、攻角α、后掠角χ的函数,一般由风洞试验获得;ε(α,χ)=0为控制方程。

1.2 约束条件

①初始约束条件为导弹投放初始时刻状态变量的初值,是给定的,即:

(2)

②终端约束是为了提高变后掠导弹对目标的攻击能力,对导弹的终端状态施加的约束,包括射程、射高和落角,即:

(3)

式中:ξx为允许的最大的射程误差,ξθ为允许的最大的落角误差。

③过程约束。

在实际的飞行过程中,过大的飞行载荷会破坏导弹弹体结构;同时,过大的动压会对导弹的热防护材料产生威胁,并影响控制系统的稳定性,故要对导弹飞行过程中的法向过载和动压加以约束,即:

(4)

④控制约束。

适当限制控制变量的变化范围可以保证变后掠导弹弹道的平滑和良好的飞行性能,即:

(5)

1.3 性能指标

变后掠导弹优化设计的一个重要的目标是在脱靶量允许的范围内保证终端速度最大,故取落速最大为目标函数,即:

J=maxv(tf)

(6)

2 优化方法

hp自适应伪谱法结合了伪谱法和hp型有限元法的优点,在精度不满足要求的区间利用双层策略决定片段宽度h和插值多项式阶次p,而在精度满足要求的区域不做变动,最大限度地保证近似精度的同时降低计算量。

2.1 最优控制问题的离散

每个单元内,插值多项式的选择方式和全局伪谱法一样,这也使得hp自适应伪谱法的最优控制问题离散和全局伪谱法相同,都将状态变量和控制变量在配置点上离散,并以各离散点为节点,利用拉格朗日插值基函数全局近似状态变量和控制变量,通过对全局插值多项式求导,近似状态变量对时间的导数,使之在一系列配点上满足动力学约束。性能指标中的积分项可以由高精度的高斯积分公式来近似,终端状态由初始状态加右函数在整个过程中积分获得[15]。

2.2 hp自适应更新方式判断准则

定义中点残差矩阵为

(7)

(8)

(9)

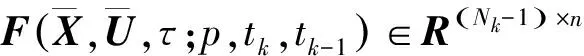
取Q中每一行残差最大值组成列向量q为

(10)

其算数平均值为

(11)

则规范化的中点残差向量为

(12)

当式(7)中的Q向量中的最大值Qm大于ε(ε为用户自定义误差),则需要细分单元或者增加多项式阶次。定义β中元素数量级的阙值为ρ,当β中存在大于ρ的元素时,称为不一致型误差,需要减小片段宽度h。一般情况下,式(12)中的β向量中大于ρ的元素总是相邻成对出现的,在这2个元素之间放置片段断点即可减小片段宽度h。图1形象地展示了是否需要放置片段断点及片段断点位置。

图1 片段断点位置

2.3 迭代流程

图2给出了hp自适应伪谱法区间划分和配点选择的迭代流程。

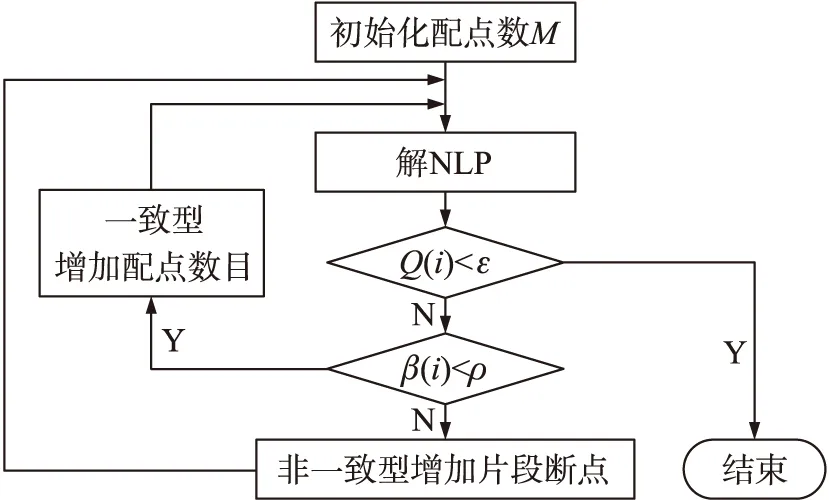
图2 迭代流程

3 仿真结果分析

3.1 仿真条件设置

导弹的质量为121.57kg,参考面积为0.018 1m2;初始条件为x0=0,y0=4km,v0=10m/s,θ0=-12.5°;末端约束为xf=10km,yf=0,θf=-65°,ξx=1m,ξθ=2°;飞行攻角|α|<10°,后掠角35°<χ<85°,动压q<70kPa,过载|ny|<4。

3.2 仿真方案

采用hp自适应伪谱法对变后掠翼导弹的后掠角和攻角进行双变量优化,并通过与已有的PSO的仿真结果对比,验证hp自适应伪谱法仿真结果的正确性。

3.3 仿真结果

图3～图8为2种优化方法的仿真结果对比,表1列出了2种优化方法的落点弹道参数。表中Δx为脱靶量。

图3 弹道曲线

图4 弹道倾角曲线

图5 攻角曲线

图6 后掠角曲线

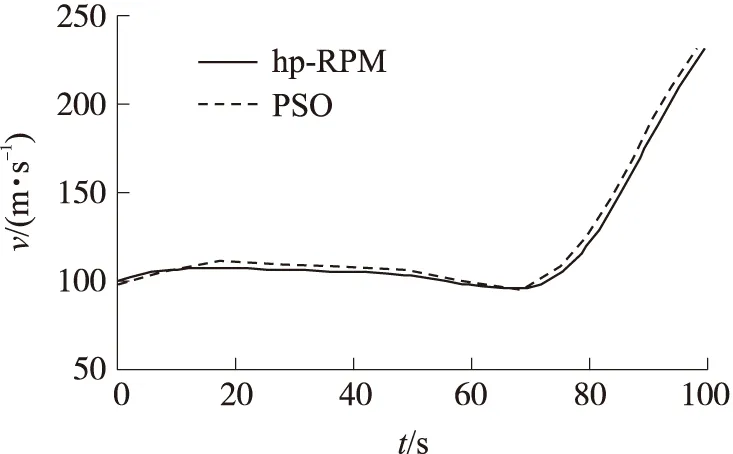
图7 速度曲线

图8 升阻比曲线

tf/sΔx/mvf/(m·s-1)θf/(°)hp-RPM99．350．5230．5-67．03PSO99．198．2229．6-67．13

从表1和图3～图8可以看出,hp自适应伪谱法和粒子群算法的仿真结果相近,验证了hp自适应伪谱法在解决基于终端速度最大的变后掠导弹优化问题上的正确性。由图3、图4、图7可以看出,在脱靶量满足精度要求的同时,终端速度达到230.5m/s,落角为-67.03°,保证了变后掠导弹以最佳的姿态攻击目标。由图6可以看出,hp自适应伪谱法和粒子群算法后掠角都是先一直是35°,而后在较短的时间内上升到85°,继而保持85°不变,即先伸展翼面增加小速度飞行的升力,后缩拢翼面减小高速飞行时的阻力,使得导弹在不同的速域内都能获得良好的飞行性能。由图6～图8可以看出,速度较小,对应展开后掠翼,增加升力;速度变大,则要收拢后掠翼,减小阻力,从而实现落速最大。

4 结束语

针对变后掠导弹的终端速度最大问题,本文利用hp自适应伪谱法对多种约束条件下的变后掠导弹进行弹道优化,采用后掠角和攻角双变量优化方案,并将得到的最优弹道与粒子群算法得到的弹道进行了对比分析,验证了hp自适应伪谱法在解决基于终端速度最大的变后掠导弹优化问题上的正确性。仿真结果表明,hp自适应伪谱法的最优弹道导弹能够在较高的命中精度的前提下,以更高的终端速度且更佳的弹体姿态攻击目标。研究成果可为变后掠导弹弹道的设计与分析提供参考。

[1] 雍恩米,陈磊,唐国金.助推-滑翔弹道的发展史及基于该弹道的制导武器方案设想[J].飞航导弹,2006(3):20-23. YONG En-mi,CHEN Lei,TANG Guo-jin.The development history of boost glide trajectory and the plan of the guidance weapon based on the trajectory[J].Aerodynamic Missile Journal,2006(3):20-23.(in Chinese)

[2]杜善义,张博明.飞行器结构智能化研究及其发展趋势[J].宇航学报,2007,28(4):773-778. DU Shan-yi,ZHANG Bo-ming.Research about intelligent vehicle structure and its development trend[J].Journal of Astronautics,2007,28(4):773-778.(in Chinese)

[3]TAKAHASHI T,SPALL R J,TURNER D C,et al.A multi-disciplinary assessment of morphing aircraft technology applied to tactical cruise missile configurations,AIAA 2004-1725[R].2004.

[4]陈元恺,董彦非,彭金京.变后掠翼身组合体阻力特性分析[J].飞行力学,2014(4):308-311. CHEN Yuan-kai,DUAN Yan-fei,PENG Jin-jing.Analysis for drag characteristic of variable swept wing-body[J].Flight Dynamics,2014(4):308-311.(in Chinese)

[5]雍恩米,陈磊,唐国金.飞行器轨迹优化数值方法综述[J].宇航学报,2008,29(2):397-406. YONG En-mi,CHEN Lei,TANG Guo-jin.Review for numerical methods of spacecraft trajectory optimization[J].Journal of Astronautics,2008,29(2):397-406.(in Chinese)

[6]王方鹏,罗竑,王海鹏.一种滑翔飞行器弹道的参数优化方法研究[J].航空制造技术,2015,(S1):104-107. WANG Fang-peng,LUO Hong,WANG Hai-peng.Research on parameter optimization method of air vehicle gliding trajectory[J].Aeronautical Manufacturing Technology,2015,(S1):104-107.(in Chinese)

[7]黄国强,陆宇平,南英.飞行器轨迹优化数值算法综述[J].中国科学:技术科学,2012,42(9):1 016-1 036. HUANG Guo-qiang,LU Yu-ping,NAN Ying.A survey of numerical algorithms for trajectory optimization of flight vehicles[J].Sci China Tech Sci,2012,42(9):1 016-1 036.(in Chinese)

[8]南英,陈市橹,严辉.航天器轨迹优化的通用数值方法[J].飞行力学,1996,14(3):20-26. NAN Ying,CHEN Shi-lu,YAN Hui.A common numerical calculation method of optimizing the trajectories of space vehicles[J].Flight Dynamics,1996,14(3):20-26.(in Chinese)

[9]李伟明,孙瑞胜,吴军基,等.变后掠翼航弹滑翔弹道优化设计[J].弹道学报,2012,24(2):6-9. LI Wei-ming,SUN Rui-sheng,WU Jun-ji,et al.Optimization of glide trajectory for aerial bomb with morphing swept wings[J].Journal of Ballistics,2012,24(2):6-9.(in Chinese)

[10]赵日,孙瑞胜,沈坚平.变后掠翼制导炸弹滑翔弹道优化设计[J].航天控制,2014,32(1):16-20. ZHAO Ri,SUN Rui-sheng,SHEN Jian-ping.The optimization design of glide trajectory for guide bomb with morphing swept wings[J].Aerospace Control,2014,32(1):16-20.(in Chinese)

[11]郭杰,唐胜景,李响,等.基于改进粒子群算法的方案飞行弹道优化设计[J].北京理工大学学报,2010,30(6):682-692. GUO Jie,TANG Sheng-jing,LI Xiang,et al.Optimum design of the project trajectory based on an improved particle swarm optimization[J].Transactions of Beijing Institute of Technology,2010,30(6):682-692.(in Chinese)

[12]GARG D.An overview of three pseudospectral methods for the numerical solution of optimal control problems[R].USA:AAS,2009.

[13]HUNTINGTON G T,BENSON D,RAO A V.A comparison of accuracy and computational efficiency of three pseudospectral methods[C]//AIAA Guidance,Navigation and Control Conference and Exhibit.South Carolina:AIAA,2007:1-22.

[14]袁宴波,张科,薛晓东.基于Radau伪谱法的制导炸弹最优滑翔弹道研究[J].兵工学报,2014,35(8):1 179-1 186. YUAN Yan-bo,ZHANG Ke,XUE Xiao-dong.Optimization of glide trajectory of guided bombs using a Radau pseudo-spectral method[J].Acta Armamentarii,2014,35(8):1 179-1 186.(in Chinese)

[15]赵日,孙瑞胜.一种变后掠翼导弹弹道快速优化方法[J].四川兵工学报,2014,35(3):41-44. ZHAO Ri,SUN Rui-sheng.Method of rapid trajectory optimization for missile with morphing swept wings[J].Journal of Sichuan Ordnance,2014,35(3):41-44.(in Chinese)

Optimization Design for Trajectory of Morphing-wing Missile Based on Hp-adaptive Pseudo-spectral Method

WANG Na,CHEN Jie-qing,MING Chao,SUN Rui-sheng

(School of Energy and Power Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to improve the final velocity of morphing-wing missile,a terminal trajectory optimization for morphing-wing missile was investigated.The sweep angle and attack angle were chosen as optimal control variables,and the trajectory optimization model was established with the multi-constraints of the dynamic pressure,the overload,and the bound conditions and so on.In view of the limitations of the global pseudo-spectral method to solve the optimal control problem with complex and multi-constraints,the hp-adaptive pseudo-spectral method combining the global pseudo-spectral method with hp finite element method was adopted to transform the trajectory optimization problem into a nonlinear programming problem,and the results were compared with those of the particle swarm optimization to confirm the correctness of the model and the method.The results show that the optimal trajectory of hp-adaptive pseudo-spectral method can ensure higher terminal speed and better attitude to attack targets with higher interception precision.

morphing-wing missile;final velocity;hp-adaptive pseudo-spectral method;trajectory optimization

2016-06-25

航空科学基金项目(20110159001)

王娜(1993- ),女,硕士研究生,研究方向为弹箭飞行制导与控制。E-mail:1395739030@qq.com。

TJ761.3

A

1004-499X(2016)04-0024-06