基于进给速度敏感点识别的NURBS曲线平滑插补算法研究

林 峰 张正红 陈 胜

1.衢州学院，衢州，324000 2.浙江永力达数控机床有限公司，衢州，324000

0 引言

NURBS为初等解析曲线／曲面和自由曲线／曲面提供了统一的数学表达形式，以NURBS为表达形式的数控代码以其良好的轮廓表征精度和精简的代码量，已得到越来越多数控系统的支持。对于现代智能化的CNC控制器而言，一个可靠高效的NURBS刀路插补控制器至关重要［1］。与基于NURBS表达的造型技术相比，基于NURBS的插补技术相对滞后，当前NURBS插补算法缺乏对曲线线形良好的自适应性。

Huang等［2］设计了恒定进给速度的插补控制方法，该方法采用一阶泰勒展开来计算指令步长下NURBS曲线上的插补点坐标。为提高计算精度，Yang等［3］提出采用二阶泰勒展开近似求解，以减小进给速度的波动。Nam等［4］提出了一种在参数曲线的始末点进行速度光滑处理，在插补曲线的中间区域保持恒定进给速度的规划方法。Altintas等［5］采用五次样条实现了有加加速度限制的插补，但该方法只在插补始末段应用，中间过程未考虑插补精度问题。Yeh等［6］实现了一种进给速率自适应的NURBS插补器，该方法根据弓高误差获得最大允许进给速度值。但该方法没有提供合适的加减速方案，在步长减小的低速区域附近，可能出现速度突变。Yong等［7］提出了离线寻找危险点的的插补算法，并对速度变化区域进行加减速控制。Shen等［8］基于进给轴伺服驱动能力角度，提出了基于轴向加速度、加加速度限制的异步插补算法。

本文提出一种基于进给速度曲线敏感点识别的NURBS插补算法。敏感点根据弓高误差在离线处理阶段确定，此后的进给速度规划即基于此已识别的敏感点。相邻敏感点之间的加减速则根据两点之间的距离进行自适应控制。进而，整个插补进给速度曲线可通过连接所有敏感点区域速度段来完成。

1 进给速度敏感点识别

众所周知，加工自由曲线时保持恒定的加工速度将无法限制弓高误差。对于给定的加工轨迹，弓高误差取决于速度曲线，本文将进给速度指令值vF下弓高误差超过给定值的点称为敏感点。因此，首先需要正确地计算弓高误差，然后进行速度曲线的正确规划。

传统方法计算弓高误差Ei时，采用局部区域的圆弧近似方法，表达式如下：

式中，Li为插补周期步长；v（ui）为C（ui）点的进给速度；T为恒定的插补周期；ρi为曲线在u＝ui处的曲率半径。

为了识别整个NURBS曲线上的敏感点，有必要在插补开始之前对整个0到1的参数空间进行离散。参数步长Δui越大，越有利于提高计算效率，但为了提高敏感点识别的精度，步长值越小越好。为了在计算效率和识别精度之间获得平衡，通过以下法则来确定参数步长Δui：

（1）初始参数步长Δui预设为Δui＝2Δui－1；

（2）如果下式满足：

式中，la为以a为起点，参数中点为终点的弦长；lb为以参数中点为起点，b为终点的弦长；lab为以a为起点，b为终点的弦长；ξ为逼近误差率。

他本来会扑到熊身上，把它杀了的。可是他的心却开始了那种警告性的猛跳。接着又向上猛顶，迅速跳动，头像给铁箍箍紧了似的，脑子里渐渐感到一阵昏迷。

则接受Δui的值，否则执行第（3）步；

在式（2）中，我们选择ξ＝1%。整个处理过程将在获得合适的参数增量Δui之后结束，并以C（ui）点离散整个NURBS曲线。

如果设定弓高误差的公差为Et，则当Ei＞Et时，C（ui）为敏感点；当Ei≤Et时，C（ui）不为敏感点。

若C（ui）是敏感点，则该点的最大允许进给速度vs可用下式定义：

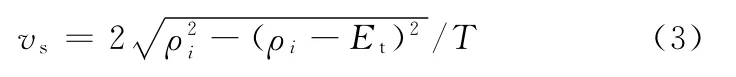
整个敏感点识别的过程不仅仅是获得一系列的敏感点信息，同时任意两个离散计算点之间的距离信息也被存储，用于后续插补规划。

2 敏感点之间的进给速度规划算法

如果敏感点存在，则进给速度不能在整个加工过程中保持恒定的vF。因此，需要在敏感点附近区域进行加减速。然而，NURBS曲线上相邻两个敏感点之间的距离是不同的，所以加减速方案需要根据不同的情况进行自适应调整。

假设两点之间的距离足够保证进给速度由vs1加速到vF以及由vF减速到vs2进行平滑加减速所需的长度，我们有必要获得完成这两个过程所需的距离。如图1所示，在加速阶段，存在ta1、ta2、ta3三个 时间阶段，分别实 现 了 Δva1、Δva2、Δva3的速度变化量。在ta1、ta3阶段，进行速度增加的同时，加速度也在变化。为保证过程的平滑性，加速度以恒定的加加速度j＝jmax进行变化。在ta2阶段，加速度保持为恒定的amax。

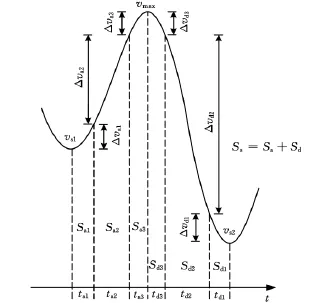
图1 加减速阶段划分（Ss＝Sa＋Sd）

首先，必须获得ta1、ta3阶段的加速时间：

式中，ta1为加速度从0变化到amax所需的时间；ta3为从amax变化到0所需的时间。

从图1可知：

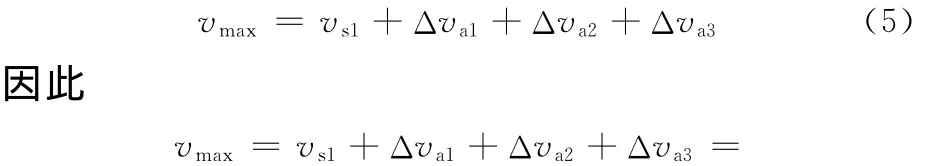
同理，对于降速阶段速度曲线，进给速度需要从vF平滑过渡到下个敏感点所需速度vs2。降速时间td1、td3的表示式为

图2 带恒定速度区域v＝vF的进给速度曲线（Ss＞Sa＋Sd）

否则，若Ss＜Sa＋Sd，则表示速度无法达到vF。此时，需要调整两敏感点之间最大速度值，vmax←vmaxη，其中，参数η设置为0.618。

重复式（4）～式（12）的计算，并校验是否满足式（12）。若不满足，则需要按上述方式进行调整。当满足式（12），保持恒定速度的时间由以下法则确定：

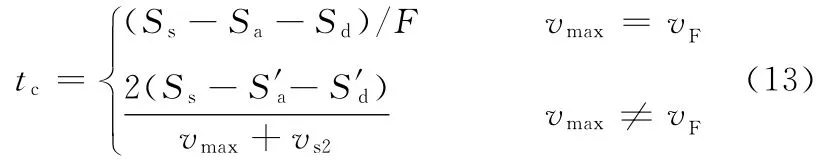
vmax≠vF时的S′a、S′d与vmax＝vF时的Sa、Sd不同，有 S′a＜ Sa，S′d＜ Sd。 从 式 （13）可 知，若vmax≠vF，并且Ss－S′a－S′d≠0，则存在一个恒速度为（vmax＋vs2）／2的安全缓冲区域（security buffer），如图3所示。如果vmax≠vF，且Ss－S′a－S′d＝0，则不存在该安全缓冲区，如图4所示。

图3 带安全缓冲区域速度曲线（Ss＜Sa＋Sd）

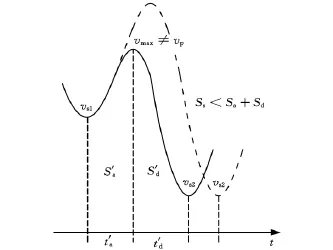
图4 不带安全缓冲区速度曲线（Ss＜Sa＋Sd）

在曲线插补的开始阶段，也必须具有加速阶段，尽管第1个插补点不必是敏感点。对于曲线末尾阶段情况也一样。但在本算法中，在曲线始末端通过设置vs＝0的方法来实现加减速控制。也即是说将始末两点视为敏感点，这样就无需设计专门的算法解决始末端的加减速问题。

3 仿真和分析

采用三次NURBS曲线来验证本插补算法的有效性。曲线控制参数如表1所示。

表1 NURBS曲线参数

示例NURBS曲线的形貌如图5所示，可以看到三个较明显的高曲率区域。事实上，在弓高误差允许值Et＝0.5μm时，这些点即为敏感点。

图5 NURBS曲线形貌

仿 真 实 验 在 vF为 80mm／s、100mm／s、140mm／s三个不同的进给速度指令值下实施。仿真使用的加工参数如表2所示。

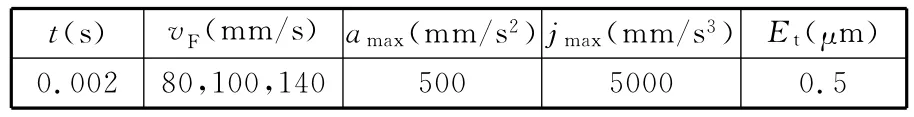
表2 加工参数

图6～图8所示为不同进给速度指令值vF条件下的插补速度vf曲线，从中可以看出，敏感点的存在与否（或者其位置）在不同的进给速度指令值条件下可能发生变化，特别地，在vf＝80mm／s以下时，该NURBS曲线不存在敏感点。

图6 vF＝80mm／s时的插补速度曲线

图9～图11所示为不同进给速度指令值vF条件下的轮廓误差。可以看出，弓高误差被严格限制在0.5μm以内。尽管在敏感点处，弓高误差和速度的预设值是通过式（3）确定的，但由于插补计算时，两点之间的距离不是严格的精确值，当插补计算到达敏感点时，实际速度已经与式（3）的预设值产生了差异。

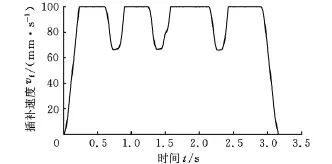
图7 vF＝100mm／s时的插补速度曲线

图8 vF＝140mm／s时的插补速度曲线

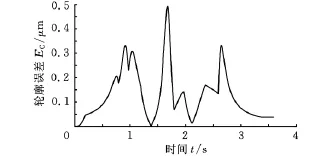
图9 vF＝80mm／s时的轮廓误差

图10 vF＝100mm／s时的轮廓误差

图11 vF＝140mm／s时的轮廓误差

4 结语

本文提出的基于进给速度曲线敏感点识别的插补方法，可以有效地确定高曲率区域的速度敏感点。在兼顾计算效率和识别准确性的问题上，本文设计了可靠的法则以确定参数步长增量。同时，设计了一套在两个相邻的速度敏感点之间进行自适应速度规划的算法，提出采用安全缓冲区的方法进行距离自适应。算法不仅考虑了插补加工的平滑性和安全性，同时兼顾加工精度和效率。NURBS插补仿真结果显示，本算法能够有效处理敏感点距离与进给速度之间存在复杂关系的不同情况。

［1］Lei W T，Sung M P，Lin L Y，et al.Fast Realtime NURBS Path Interpolation for CNC Machine Tools［J］.International Journal of Machine Tools ＆Manufacture，2006，43：1－12.

［2］Huang J，Yang D.A Generalized Interpolator for Command Generation of Parametric Curves in Computer Controlled Machines［C］／／ASME Japan／USA Symposium on Flexible Automation.San Francisco，CA，USA，1992：286－292.

［3］Yang D，Kong T.Parametric Interpolator Versus Linear Interpolator for Precision CNC Machining［J］.Comput－Aided Design，1994，26（3）：225－233.

［4］Nam S H，Yang M Y.A Study on a Generalized Parametric Interpolator with Real－time Jerk－limited Acceleration［J］.Computer－Aided Design，2004，36（1）：27－36.

［5］Erkorkmaz K，Altintas Y.High Speed CNC System Design.Part I：Jerk Limited Trajectory Generation and Quintic Spline Interpolation［J］.International Journal of Machine Tools ＆ Manufacture，2001，41：1323－1345.

［6］Yeh S，Hsu P.Adaptive－feedrate Interpolation for Parametric Curves with a Confined Chord Error［J］.Computer－Aided Design，2002，34（2）：229－237.

［7］Yong T，Narayanaswami R.A Parametric Interpolator with Confined Chord Errors，Acceleration and Deceleration for NC Machining［J］.Computer－Aided Design，2003，35（13）：1249－1259.

［8］Shen Hongyao，Fu Jianzhong，Chen Zichen.Axisbased Look－ahead Interpolator for Machining of Surfaces Represented by Nurbs Curves［J］.Machining Science and Technology，2008，12（4）：546－562.