自抗扰算法在直流力矩电机伺服系统中的应用

龙满林 付永领 李光华 陈双桥

1.北京航空航天大学，北京，100191 2.海军工程大学，武汉，430033

0 引言

直流力矩电机因具有力矩电流比率高、过载能力强、可靠性高、控制简便等特点，被广泛应用于伺服控制中。为了进一步提高直流力矩电机伺服系统性能，学者们进行了诸多研究。研究结果表明，对于高精度伺服系统而言，摩擦力矩是影响系统伺服性能的主要因素。这是因为摩擦力矩具有非线性、不确定性、滞后性的特点，直接恶化伺服系统的动静态性能，造成伺服系统低速运动时爬行、速度过零时波形畸变、存在稳态误差或振荡［1］，因此，大多数学者把研究重点放在了消除摩擦力矩影响上，提出了许多摩擦补偿方法。基于摩擦超前补偿模型的PID控制方法是其中最具代表性的补偿方法，该方法仅考虑摩擦力矩的影响，需要建立精确的摩擦模型。摩擦模型的研究主要集中于静态Stribeck模型和动态LuGre模型，而这两种模型中需要辨识的参数多而且部分不可测，所以难以确保模型的精确性并给出精确的补偿值。文献［2］在静态Stribeck模型基础上，提出了自适应摩擦补偿算法。该算法依赖于一些状态变量的重构，而且控制律复杂，实际应用效果受到影响。文献［3］利用遗传算法寻优的功能辨识动态LuGre模型的参数，该算法在实际应用中存在两个缺陷：①若种群规模过小，则会影响寻优的效果；②若种群规模过大，则过长的算法运行时间难以实现在线优化。此外，由于摩擦力矩是速度的函数，直流力矩电机超低速运行和过速度零点时得不到精确的速度信号，所以难以建立摩擦模型。这些原因都会降低摩擦模型的精度，直接恶化伺服性能。

此外，影响直流力矩电机伺服系统精度的因素还有电机周期性波动力矩、模型参数时变特性、负载波动和反馈元件误差等。这些影响因素在仿真中很难建立精确模型，在实际使用时不能采用常规算法进行估计预测，因而不可能给出准确的补偿值，致使系统不能获得高的伺服精度。为了提高伺服精度，应对这些内在或外加的不利影响因素进行有效的消除或补偿。

因此，为了使直流力矩电机伺服系统达到期望的伺服精度，必须综合考虑摩擦力矩、电机周期性波动力矩、模型参数时变特性、负载波动和反馈元件误差等因素的影响，缺一不可。然而，它们各自的精确模型很难建立，更不可能实时获得精确的补偿值。针对这一难点，本文引入自抗扰算法，该算法可以将摩擦力矩、电机周期性波动力矩、模型参数时变特性、负载波动和反馈元件误差等影响因素总和成唯一的总扰动，构造扩张状态观测器，实时观测重构并补偿这一总扰动。只要准确补偿了总扰动，伺服系统的控制精度就能得到大幅提高。

1 直流力矩电机伺服系统特性分析

北京航空航天大学流体传动与控制技术研发中心配备有某型进口三轴电液复合飞行仿真转台，其内框是典型的直流力矩电机伺服系统。本文以该系统为例，仅从控制角度出发，引入自抗扰算法，以期进一步提高系统的伺服精度。该伺服系统的结构如图1所示，其控制原理为：测速电机测得的角速度信号和光电编码器测得的角位移信号经数据采集卡输入到工控机中，与相应的期望值相减得到误差，这些误差按照控制算法经过A／D转换生成控制电压U，控制电压U 经PWM功率放大板放大成均值电压为Um的PWM方波，PWM方波驱动直流力矩电机，使其带动转台内框及负载一起转动，转角为θ。

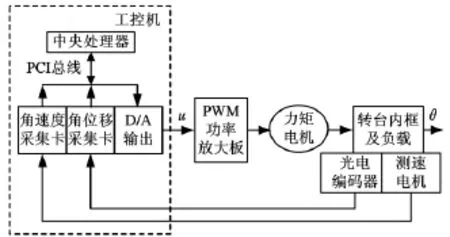
图1 直流力矩电机伺服系统硬件构成示意图

针对图1，建立直流力矩电机伺服系统的数学模型。电机的电压、转矩、负载的数学模型［4］分别如下：

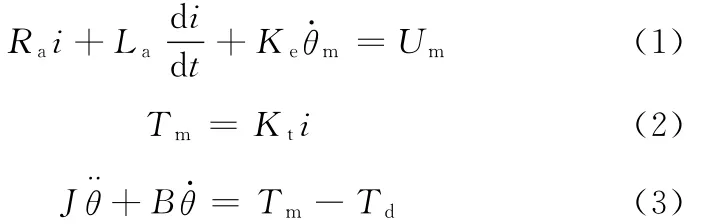
式中，Ra为电枢电阻；La为电枢电感；i为电枢电流；Ke为反电动势系数；θm为电机转角；θ为内框转角，θ＝θm；Tm为电机输出力矩；Kt为电磁转矩常数；J为等效到电机轴的转动惯量（包含负载的转动惯量在内）；B为等效的黏性阻尼系数；Td为总扰动，包含摩擦力矩、电机周期性波动力矩、模型参数时变特性、负载波动和反馈元件误差等影响因素。

对式（1）～式（3）进行拉氏变换，消除中间变量，得到系统的传递函数方框图（图2）。控制器取位置差形成控制律f（θr－θ）。KPWM为PWM功率放大器的放大比例系数。从图2可以看出，Td中的每一分项都与直流力矩电机直接关联，对伺服精度都有影响，在仿真和实验中必须消除。

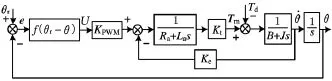
图2 直流力矩电机伺服系统传递函数方框图

2 自抗扰算法设计

基于自抗扰算法的控制器由跟踪微分器、扩张状态观测器和反馈控制律三部分组成。跟踪微分器根据系统的控制性能要求，安排期望输入θr的系统过渡过程，以避免系统超调，同时产生期望输入的微分信号。扩张状态观测器估计系统的状态变量和总扰动。反馈控制律依据扩张状态观测器和微分跟踪器给出的实时值构造控制量U，以补偿总扰动Td。由于图2中的直流力矩电机伺服系统已经简化为二阶系统，故自抗扰控制器中的扩张状态观测器增加一阶，用来估计系统的总扰动Td。针对此系统设计的自抗扰控制器如图3所示。

2.1 跟踪微分器设计

跟踪微分器为直流力矩电机伺服系统的期望输入θr安排过渡过程，得到光滑的输入信号v1及其微分信号v2。跟踪微分器的离散算法如下［5］：

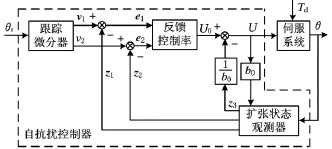
图3 直流力矩电机伺服系统自抗扰控制器结构图

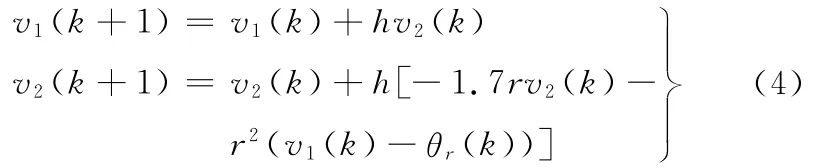
其中，h为仿真中的步长，实际控制中的采样时间；r为速度因子，决定跟踪的快慢，r越大，过渡过程越快，此参数需要被整定。

2.2 扩张状态观测器设计

构造扩张状态观测器得到伺服系统的状态z1、z2和总扰动的实时作用量z3。扩张状态观测器的离散算法如下：

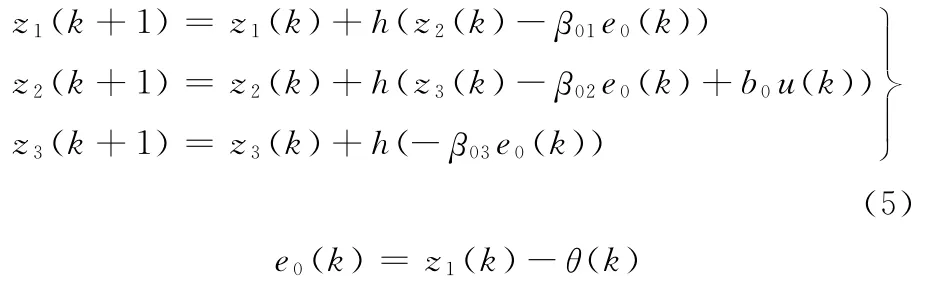
其中，z1为对直流力矩电机伺服系统转角θ的估计；z2为对直流力矩电机伺服系统转角的微分估计，为控制律的生成提供微分信号，用来构造误差的微分；β01、β02、β03、b0为可调参数，需要被整定。

2.3 反馈控制律设计

状态误差反馈控制律是利用跟踪微分器输出和扩张状态观测器输出之差，即广义输入与伺服系统的广义输出之间的误差产生伺服系统所需要的控制量对总扰动Td进行实时补偿。其功能相当于用反馈线性化方法，将直流力矩电机伺服系统由非线性系统转化为“积分器串联型”系统。反馈控制律的离散算法如下：

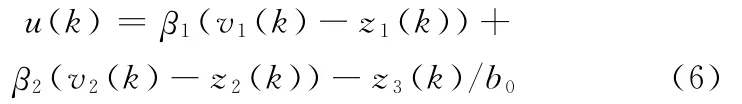
其中，β1、β2为控制器参数，需要被整定。

3 仿真研究

纵观自抗扰控制器，共有7个参数需要被整定。为了整定这些参数，需要对直流力矩电机驱动的转台内框进行仿真。仿真中，摩擦力矩采用静态Stribeck模型［1］，表达式如下：

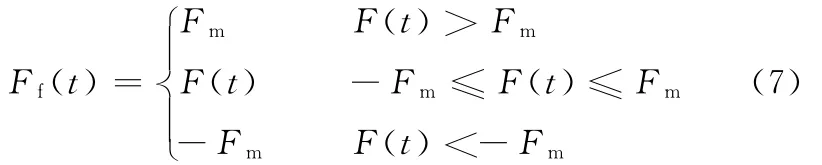
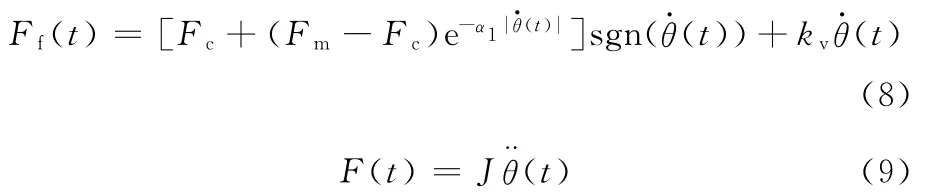
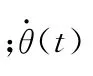
电机周期性波动力矩、模型参数时变特性、负载波动和反馈元件误差等非线性和随机性影响因素引起的扰动用随机值rand（1）来表示，那么，总扰动用下式表示：

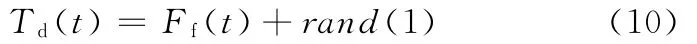
期望输入选用正弦函数，表达式用下式表示：

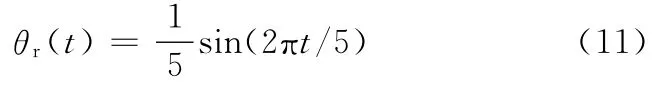
直流力矩电机伺服系统相关参数值为Ra＝0.7Ω，La＝7mH，Kt＝ 2.95N · m／A，Ke＝2.9V·s／rad，J＝3.2kg·m2，B ＝0.01N·m·s／rad，KPWM＝2.65。静态Stribeck模型参数为Fc＝3N·m，Fm＝5N·m，α1＝1，α＝0.01，kv＝2N·m·s／rad。经过多轮仿真实验，对比分析仿真结果，使跟踪误差的方差最小的自抗扰控制器参数经取整后为β01＝15，β02＝15 000，β03＝10，β1＝300，β2＝50，b0＝12，r＝500。仿真结果见图4。图4中，总干扰Td在［－8，8］N·m的范围内变化，其值过零点时正负号交替，且发生突变，这是由于直流力矩电机运动方向改变导致摩擦力矩换向所致。跟踪曲线中实际输出曲线与期望输入曲线吻合，未出现常规PID控制中容易出现的极限环、平顶等不良现象［1］。控制电压在直流力矩电机刚开始运动时波动较大，当直流力矩电机启动后，控制电压在［－1.5，1.5］V的范围内波动。跟踪误差曲线在［－0.6×103，0.6×103］rad范围内波动。从跟踪曲线和跟踪误差曲线上看，伺服控制的效果好。

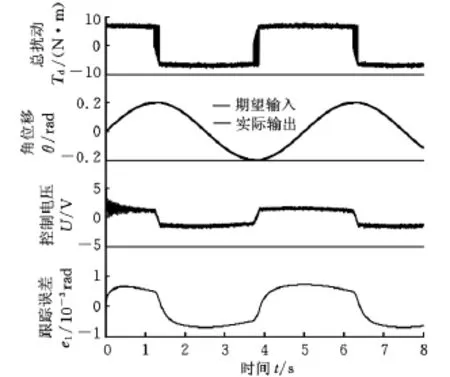
图4 仿真结果

4 实验研究

将仿真中整定的控制器参数直接应用到直流力矩电机驱动的转台内框上，期望输入为式（11），实验结果见图5，从跟踪曲线来看，控制效果好。不改变控制器参数，也不改变期望输入的幅值，逐渐增加期望输入的频率，最高跟踪频率达2Hz，2Hz时的跟踪曲线见图6。超过2Hz后，跟踪效果不佳。因此，在同一组控制器参数的作用下，系统跟踪频率在0.2～2Hz范围内的正弦信号的效果良好。不改变控制器参数，期望输入信号的频率仍为0.2Hz，逐渐增大期望输入的幅值到1rad，跟踪曲线见图7，跟踪效果仍然很好。

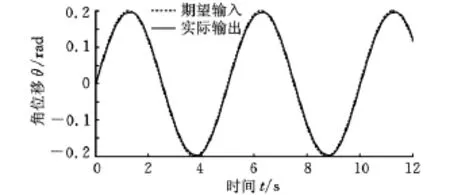
图5 实验结果

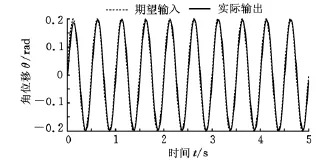
图6 实验结果

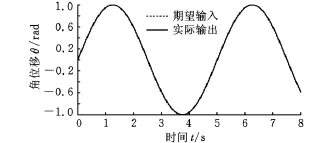
图7 实验结果

从图5～图7的实测结果可以看出，在保持自抗扰控制器的7个参数不变的情况下，在较大范围内改变期望输入，跟踪效果仍然很好，说明自抗扰算法的鲁棒性强。

5 结语

从仿真和实验的结果可知，利用自抗扰算法对直流力矩电机伺服系统进行控制时，可将影响伺服系统跟踪精度的内在或外在的影响因素总和成一个综合的外部扰动，即总扰动，并对其进行实时估计和补偿。这种控制方法不用分析影响因素的特性，也不用费时费力地建立应用效果不佳的模型。自抗扰算法的难点在于控制器参数的整定。可采用针对系统的名义模型在苛刻的干扰条件下进行仿真研究的方法整定控制器参数，参数的优化过程可借助于如遗传算法之类的优化方法。当参数被整定后，对于仿真条件或实际系统在一定范围内发生变化的情况，自抗扰算法均具有良好的应用效果，据此可见自抗扰算法鲁棒性强，具有优良的工程应用性。

［1］刘金锟.先进PID控制 MATLAB仿真［M］.2版.北京：电子工业出版社，2007.

［2］王忠山，王毅，苏宝库.一种精密转台系统自适应摩擦补偿方法［J］.华南理工大学学报（自然科学版），2007，35（9）：55－59.

［3］焦竹青，屈百达，徐保国.基于遗传算法的直流伺服电机的摩擦补偿［J］.清华大学学报，2007，47（2）：1875－1879.

［4］牛建军，付永领，刘和松.高精确度飞行仿真转台内框控制摩擦补偿研究［J］.电机与控制学报，2008，12（5）：576－579.

［5］史永丽，侯朝桢.基于自抗扰控制的伺服系统摩擦补偿研究［J］.计算机工程与应用，2007，43（29）：201－203.