波纹管用于水下仪器设备压力平衡的力学性能分析
刘焕进 刘正士 王 勇 毕 嵘 陈恩伟
合肥工业大学,合肥,230009
0 引言
在深海(3000m以下)环境下进行作业的水下仪器设备会面临海水的大压力问题,压力平衡(压力补偿)技术是解决这一问题的有效途径[1]。
目前,国内外的压力平衡技术主要是利用弹性元件(如膜片、软囊、波纹管等)在水压力作用下产生弹性变形,使得充油(压力平衡用油液)的水下仪器设备内部的油压与外部海水的压力趋于平衡,仪器设备的壳体承受的压差减小,从而可以减小仪器设备壳体的壁厚,使仪器设备变得轻巧[2]。
文献[3-4]将波纹管用于在高温高压环境下工作的石油测井仪器的压力平衡;文献[5]将波纹管与外置弹簧相串联,用于深海水下液压系统的不间断液压源;文献[6]提出了一种发明专利,将波纹管用于在深海环境下使用的蓄电池的压力平衡。但这些文献均没有对波纹管在深海大压力作用下的力学特性作进一步分析。
在深海大压力环境下,仪器设备内部的油液将产生不可忽略的较大压缩,使压力平衡用波纹管产生大挠度变形,这一变形会抵消掉一部分水压,从而导致仪器设备的内外压力之间存在一个压差。这一压差的存在会导致水下仪器设备产生压缩变形,如果压差过大,有可能使仪器设备的壳体遭到破坏。同时,波纹管的性能取决于其波型参数,波纹管的压力平衡能力与波型参数之间也必然存在一定的关系。因此,有必要对波纹管在深海大压力环境下的力学性能进行深入研究和分析,找出其内外压差与仪器设备的结构以及波型参数之间的关系,为改善波纹管的压力平衡效果、改进水下仪器设备的结构设计提供理论依据。
本文采用非线性有限元方法,基于液体的可压缩性,分析了波纹管在深海大压力环境下的非线性力学行为,提出了仪器设备内外压差的计算方法和计算流程,研究了波纹管的压力平衡能力与相关因素之间的关系,总结了波纹管式压力平衡结构的设计原则。
1 波纹管式压力平衡原理简介
波纹管式压力平衡结构如图1所示。假设仪器设备的外形为圆柱形,仪器内部充满压力平衡用的绝缘油液。在上端盖的中心留有通孔,该通孔与波纹管内部相通,外部海水经由通孔进出波纹管内部。波纹管的一端固定在仪器的上端,另一端在压差的作用下可自由伸缩。由于波纹管与内部油液之间没有间隙存在,故波纹管随油液的体积变化而产生变形,且波纹管的体积变化量与油液的体积变化量相同。当海水压力增大时,波纹管受内压产生拉伸,油液的体积变小,压力增大,自动与外部海水压力相平衡;当海水压力减小时,波纹管受外压产生压缩,油液的体积变大,压力减小,最终达到与外部海水压力相平衡。
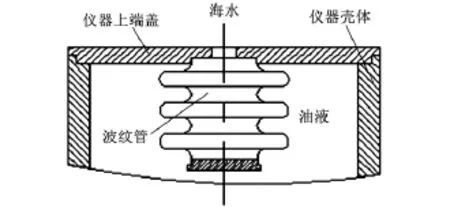
图1 波纹管式压力平衡结构示意图
2 波纹管式压力平衡的非线性力学行为分析
2.1 波纹管非线性力学行为分析方法
对波纹管进行性能分析的方法常用的有解析法、工程近似法以及数值方法。解析法难以用于波纹管的非线性问题的求解,求解过程较为复杂;工程近似法仅在波纹管处于小变形状态下能得到相对精确的结果;数值法主要包括有限元法、有限差分法、边界元法等,目前,广泛应用的是有限元法[7-11]。有限元法可以较为精确地模拟分析波纹管的非线性特性,可以得到各节点的位移、应力、应变等性能参数。
考虑压力平衡用波纹管在深海大压力环境下会处于大挠度变形状态,为对其非线性力学行为进行较为精确的分析,在此选用非线性有限元方法,并在分析中考虑波纹管的大位移、小应变的几何非线性特性[12-13]。
由于波纹管具有轴对称的几何造型,用于压力平衡时仅承受内外压差作用,在许可位移范围内其变形后的几何形状也具有轴对称性,因此,为了降低计算量,可以取其1/4实体模型进行分析,图2所示为在ANSYS有限元分析软件中建立的波纹管实体模型。
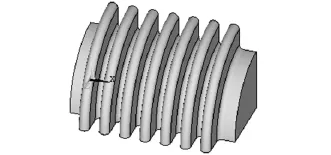
图2 1/4波纹管实体模型
牛顿-拉斐逊迭代法(Newton Raphson)和载荷增量法是利用有限元求解非线性问题时最常用的方法。牛顿-拉斐逊法对某些非线性问题可能会产生不收敛的问题,而载荷增量法则有可能使求解结果偏离正确解。为克服各自的缺点,常将两种方法结合起来,将整个载荷分解成多个小的载荷增量,在每一级载荷水平上均采用牛顿-拉斐逊法进行迭代,以求得精确的平衡状态,这样既保证了计算精度,也提高了收敛速度[7,14-15]。
2.2 波纹管的允许位移
波纹管在实际工作过程中,如果在外力作用下产生的位移量过大,波纹管会产生塑性变形(又称残余变形),这将严重降低波纹管的精度、稳定性、可靠性及其使用寿命,因此,波纹管在外力作用下产生的最大位移所引起的应力的等效应力不应超过材料的屈服强度[16]。
在将波纹管用于水下仪器设备的压力平衡时,必须进行合理的设计和选型,既要保证波纹管在压力载荷下能产生足够大的位移量,以满足压力平衡性能的要求,又要保证波纹管的最大位移不超过其允许位移。
2.3 计算波纹管变形所引起的体积变化
波纹管变形后的形状比较复杂,很难根据其有效面积[16]来精确地计算体积变化。为此,可利用数值积分方法来求其体积变化。
如图3所示,节点i和节点i+1之间沿波纹管轴向的距离为Δxi,两节点到波纹管轴线的径向平均间距为ri,则由图中节点i和节点i+1之间的阴影部分构成的多边形绕波纹管轴线一周所包围的体积可近似表示为

由此可得到波纹管的总体积为

式中,N为轴向节点的个数。
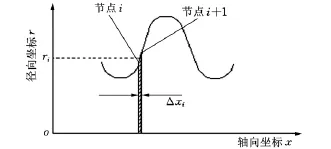
图3 波纹管体积计算的数值解法
按照上述方法求得波纹管变形前后的体积,两者的差值即为波纹管变形所引起的体积变化ΔV。
2.4 仪器设备工作水深与内外压差的关系
设某一深度处的海水压力为p,传感器内部油液的初始压力为常压p0,油液的初始体积为V0,油液的体积弹性模量为K,则传感器内部油液在海水压力作用下的体积压缩量为

海水深度和海水压力的关系为

式中,g为重力加速度;H为海水深度;ρ为海水的密度。
波纹管和内部油液之间没有空隙,油液的体积变化与波纹管变形所产生的密封体积变化相同,即

据此可以求得传感器所工作的水深与内外压差以及波纹管体积变化的关系为
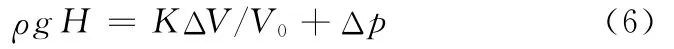
2.5 内外压差的计算流程
仪器设备在某一深度的海水环境下工作,由于波纹管的压力平衡作用,仪器设备的内外压力趋于平衡。同时,由于波纹管的变形抵消了一部分水压,故存在一个内外压差。为了计算这个压差,采用逐步迭代的方式进行求解,计算流程如图4所示。

图4 波纹管内外压差的计算流程
首先,给波纹管施加初始压力载荷,利用有限元分析软件计算波纹管的变形,然后根据式(2)计算波纹管变形前后的体积,从而求得其体积变化;根据式(6)计算仪器的工作水深,如果水深比设定的值小,则增大波纹管的压力载荷,重复上述步骤,直至工作水深达到设定值,这时施加在波纹管上的压力载荷即为在设定的工作水深下仪器的内外压差。
3 算例
3.1 相关参数
以充油式深海压力传感器为研究对象,设传感器的外形为圆柱形,在3000m深的海水环境下工作,传感器半径Rc=50mm,长度L=100mm。U形波纹管的参数为:外径D=53.5mm,内径d=37.5mm,壁厚h0=0.1mm,波距t=6mm,波厚a=3mm,波纹数n=7;波纹管的有效长度L0=39mm,总长度(包含两端接口的长度)L=49mm。波纹管材料选用在海水环境下具有优良的抗腐蚀性能的1Cr18Ni9Ti不锈钢材料,其弹性模量E=195GPa,泊松比为0.3。传感器内部油液体积占传感器总体积的比例为K0=0.7,油液的体积弹性模量K=1700MPa。
3.2 波纹管变形及内外压差
按照图4所示的波纹管内外压差计算流程,利用MATLAB软件和ANSYS有限元分析软件,通过迭代计算得到如下结果:波纹管的内外压差Δp=28.78kPa时,传感器的工作水深H=2999.7m,相对误差为0.01%。这时,波纹管自由端的轴向位移为5.899mm,波纹管变形所引起的体积变化ΔV=9735.2mm3,油液的体积压缩量为9736.3mm3,最 大 von Mises等 效 应 力 为320MPa。进一步分析可知,当传感器的内外压差Δp=68kPa时,波纹管的最大von Mises等效应力为588MPa,达到材料的屈服强度。这时波纹管自由端的轴向位移为9.762mm,达到其允许位移,传感器可工作的最大水深为4975m。
3.3 波纹管的压力平衡能力与相关因素的关系
图5反映了传感器工作水深与内外压差之间的关系。从图5可以看出,当H=100m时,Δp=650Pa;当 H=1000m 时,Δp=6.75kPa;当 H=3000m时,Δp=28.78kPa。表明随着仪器工作水深的增大,波纹管的位移补偿量增大,内外压差也随之变大。因此,必须对波纹管进行严格的选型和设计,仪器设备选择合理的形状尺寸,以使仪器设备的内外压差减小到容许范围。
图6反映了波纹管的壁厚h0与内外压差Δp之间的关系。从图6可以看出,当h0=0.15mm时,Δp=69.5kPa;当 h0=0.1mm 时,Δp=28.78kPa;当h0=0.06mm 时,Δp=10.85kPa。表明壁厚越小,波纹管的压力平衡能力越强。但壁厚越小,波纹管的承压能力就越小[16]。因此,在满足波纹管承压能力的前提下,壁厚应尽可能地小。
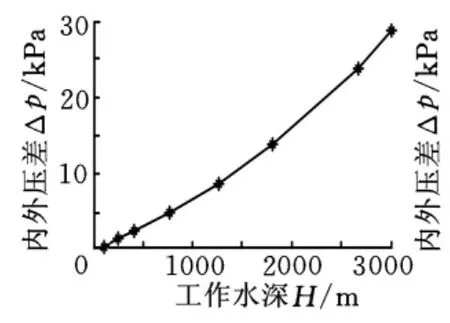
图5 工作水深与压差的关系
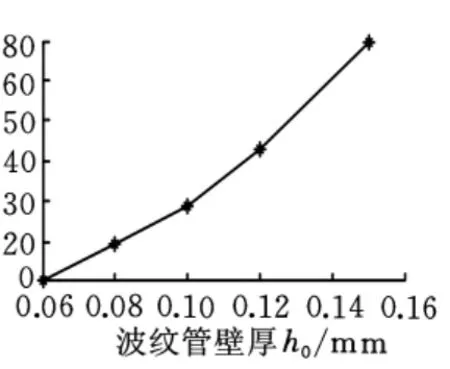
图6 波纹管壁厚与压差的关系
图7反映了传感器内部油液体积占传感器总体积的比例K0与内外压差之间的关系。从图7可以 看 出,当K0=0.7 时,Δp=28.78kPa;当K0=0.5时,Δp=17.95kPa。表明内部油液体积所占比例越小,传感器的内外压差也越小。因此,仪器内部的油液应尽可能地少。
图8反映了波纹管的波高h与内外压差之间的关系。从图8可以看出,当h=3mm时(环板宽度为0),Δp=322.5kPa;当h=4mm 时(环板宽度为1mm),Δp=146.5kPa;当h=8mm时(环板宽度为5mm),Δp=28.78kPa;当h=12mm时(环板宽度为9mm),Δp=16.2kPa。表明波高(环板宽度)对波纹管的压力平衡能力有显著的影响。波高越大(环板越宽),波纹管的压力平衡能力越强,但当波高增大到一定程度后,它对内外压差的影响减小。但波高增大,波纹管的成形难度也相应增大[16]。因此,应综合考虑波纹管的波高与成形难度的关系,合理地选择波高。
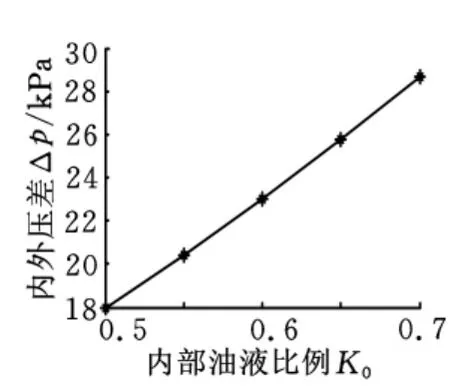
图7 内部油液所占比例与压差的关系

图8 波纹管波高与压差的关系
图9反映了波纹管的外径D与内外压差之间的关系。从图9可以看出,当D=40mm时,Δp=235.5kPa;当D=60mm 时,Δp=15.5kPa;当D=80mm时,Δp=3.95kPa。表明波纹管的外径对其压力平衡能力也有显著的影响。外径越大,波纹管的压力平衡能力越强。但当外径增大到一定程度后,波纹管对内外压差的影响减小。因此,通过增加波纹管的外径来调节内外压差是有限制的。
图10反映了波纹管的有效长度L0与内外压差之间的关系。从图10可以看出,当L0=39mm时,Δp=28.78kPa;当 L0=57mm 时,Δp=17.3kPa。表明随着波纹管有效长度的增大,内外压差减小,其压力平衡能力增强。但是,波纹管有效长度会影响波纹管的稳定性[16],有效长度增大,波纹管的稳定性就会降低,这一点在选择有效长度时必须加以考虑。
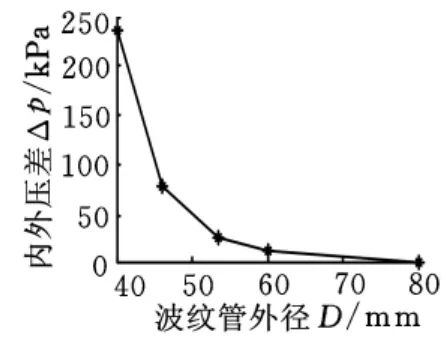
图9 波纹管外径与压差的关系
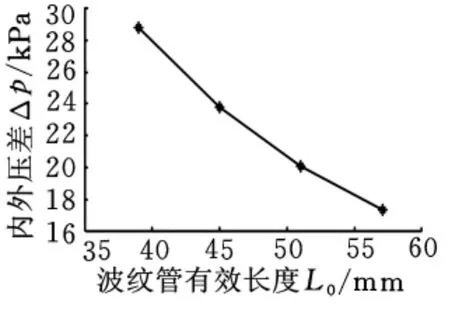
图10 波纹管有效长度与压差的关系
图11反映的是波纹管的波纹数n与内外压差之间的关系。在波纹管的有效长度不变的情况下,增加波纹管的波纹数,则波纹管的波距t相应地减小。从图11可以看出,当波纹数n=7(波距t= 6mm)时,Δp =28.78kPa;当n=9(波距t= 4.6mm)时,Δp =19.3kPa。表明随着波纹数的增加(或者说随着波距的减小),波纹管的内外压差减小,其压力平衡能力增强。考虑波纹管的成形难度,由于内径小的波纹管成形困难,因此波距占内径的百分比应随内径的增大而减小[16]。故在满足成形工艺要求的前提下,应尽可能增加波纹管的波纹数(减小波纹管的波距)。
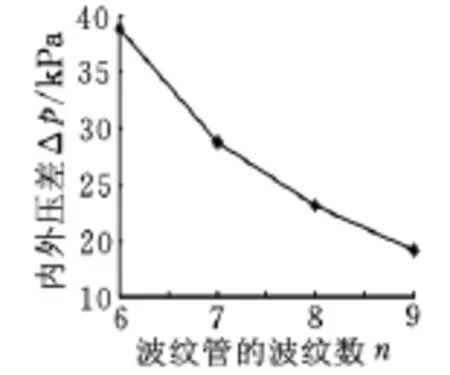
图11 波纹数与压差的关系
4 波纹管式压力平衡结构的设计原则
基于以上分析,可以归纳出波纹管式压力平衡结构的设计原则:
(1)在结构尺寸允许的范围内,波纹管的直径应尽可能大。在满足稳定性的前提下,波纹管的有效长度应尽可能大。
(2)在满足工艺要求的前提下,波纹管应尽可能选择较小的壁厚。但壁厚越小,波纹管的承压能力越差,从而影响其允许位移,故必须综合考虑。
(3)在波纹管的有效长度一定的情况下,应尽可能选择较小的波距或较大的波纹数。
(4)在满足工艺要求的前提下,波纹管应选择较大的波高(较宽的环板)。
(5)仪器设备的结构要紧凑,内部油液要尽可能地少。
(6)波纹管的材料应选择在海水环境下抗腐蚀性能好的不锈钢材料。
5 结论
(1)利用非线性有限元法来分析压力平衡用波纹管的力学性能,提出的仪器设备内外压差的计算方法和计算流程可用于压力平衡用波纹管的设计分析计算。
(2)仪器设备内部油液在深海大压力环境下会产生较大体积变化,压力平衡用波纹管的变形所引起的仪器设备内外压差随水深的增大而增大,在实际应用中必须加以考虑。通过对波纹管以及仪器设备进行结构优化设计可减小这一内外压差,提高波纹管的压力平衡能力。
(3)总结了波纹管式压力平衡结构的设计原则,可为基于波纹管式压力平衡的水下仪器设备的结构设计提供指导。
[1]王勇,刘正士,陈恩伟,等.膜片式水下力传感器力学特性与设计原则分析[J].中国机械工程,2008,19(15):1774-1777.
[2]王勇,刘正士,陈恩伟,等.软囊式水下力传感器的力学特性与设计原则[J].机械工程学报,2009,45(10):15-21.
[3]毕华壮,欧阳洋.井下仪器的压力平衡及补偿设计[J].声学与电子工程,2004(3):36-37.
[4]赵旻昕.石油测井仪器的耐高压设计[J].石油仪器,2009,23(2):12-14.
[5]张俊,顾临怡,邱会强,等.波纹管型深海水下不间断液压源的研究[J].液压与气动,2004(6):62-66.
[6]Bo O(Tanem NO).Capacitor Arranged in a High Pressure Environment:US,12/602175[P].2010-08-19.
[7]朱卫平,黄黔.旋转壳在子午面内整体弯曲的几何非线性摄动有限元及在波纹管计算中的应用[J].应用数学和力学,2002,23(12):1227-1240.
[8]刘岩,段玫,张道伟.波纹管应力分析研究进展[J].管道技术与设备,2006(4):31-33.
[9]马伟,李德雨,钟玉平.波纹管的发展与应用[J].河南科技大学学报(自然科学版),2004,25(4):28-31.
[10]万宏强,汪亮.低温环境下波纹管的轴向刚度计算[J].机械强度,2009,31(5):787-790.
[11]张庆,王华坤,王心丰.U型波纹管稳定性非线性有限元分析[J].南京理工大学学报,2002,26(3):270-273.
[12]姜宏春,蔡纪宁,张秋翔,等.机械密封用挤压成型金属波纹管应力及轴向刚度的有限元分析[J].化工设备与管道,2007,44(5):13-17.
[13]周毅锦,李庆生.波纹管非线性特性的有限元分析[J].南京化工大学学报,1999,21(4):61-64.
[14]沈玉堂,李永生.波纹管非线性有限元分析及其软件开发[J].管件与设备,2003(1):17-19.
[15]罗喜恒,肖汝诚,项海帆.几何非线性问题求解的改进算法[J].公路交通科技,2005,22(12):75-77.
[16]徐开先.波纹管类组件的制造及其应用[M].北京:机械工业出版社,1998.

