含精英策略的小生境遗传退火算法研究及其应用

刘爱军 杨 育 邢青松 陆 惠 张煜东

1.重庆大学机械传动国家重点实验室，重庆，400030 2.西南交通大学，成都，610031

3.上海师范大学，上海，201815 4.哥伦比亚大学，纽约，美国，10032

0 引言

生产调度是一个交叉性研究领域，涉及数学、控制工程、工业工程等多个学科，其主要任务是在有限的资源约束下，确定工件在相关设备上的加工顺序，以保证所选定的生产目标最优。生产调度的核心内容是算法设计，主要包括算法编码、种群初始化、操作逻辑等抽象问题的算法实现过程。高效稳定的算法研究与应用，是实现先进制造和提高生产效益的基础与关键。目前，已发展了包括遗传算法、模拟退火算法、免疫算法等多种人工智能算法，但这些算法各自存在性能上的缺陷，同时，在复杂优化问题求解方面，单一算法的优化结果往往不理想，因此，算法的融合成为提高算法性能的一个重要且有效的途径。

国内外学者选择优化领域应用最为广泛的遗传和退火算法进行研究，以期改善算法性能。梁旭等［1］提出了并串混联结构的遗传退火算法，该算法综合了遗传算法（GA）全局并行和退火算法（SA）局部串行的搜索特点，增强了系统的全局和局部搜索能力，但该算法没有解决在搜索初期由于采用比例选择算子导致的优良个体急剧增加致使种群失去多样性的问题。张昊等［2］提出了一种自适应模拟退火遗传算法，将模拟退火算法嵌入到自适应遗传算法的循环体中，解决了遗传算法局部搜索能力较差、容易陷入局部最优解等问题，采用自适应交叉和变异操作，解决了进化过程中因交叉和变异概率不变所导致的收敛速度慢的问题，该算法依然没有解决搜索初期有效基因缺失的问题。潘全科等［3］采用4－2选择代替常用的转轮选择方式，进化中，被选择的2个个体经过遗传操作产生2个新的个体，然后从这4个个体中选择生产周期不同的2个优秀个体进入下一代，这样既有利于保留优秀个体，又有利于维持群体的多样性，克服了转轮选择易造成群体中模式单一的缺陷，但这种改进的选择方式在提高算法性能的同时，额外增加了算法的复杂度和运算资源的消耗。刘敏等［4］针对遗传算法变异概率固定不变的缺陷，提出了自适应变异概率，针对选择算子对种群多样性的影响，提出用整体退火选择的方式选择杂交母体，避免种群早熟化，这种概率选择机制部分地改善了搜索初期有效基因的缺失问题，但因优化过程中没有充分利用进化历史信息，故要实现较好的优化效果依然需要较长的搜索过程。冯毅等［5］提出了基于混合策略的3层并行搜索算法，混合算法在各温度下依次进行GA、SA和小生境搜索。其中，SA的初始解来自GA的进化结果，经Metropolis抽样过程得到的解与GA的结果一起构成小生境的处理群体，处理结果又成为GA进一步优化的初始种群。这种融入了小生境技术的改进算法虽然算法性能得到改善，但依然没有克服交叉和变异概率在整个搜索过程中固定不变所导致的求解过程长的缺陷，同时，优化过程也没有充分利用历史信息。

综上所述，目前具有代表性的遗传退火算法的研究成果，均强调通过融合的思想来实现算法的优势互补，以达到改善算法性能的目的。但上述诸算法在进化过程中明显缺乏种群间历史信息的交流与反馈，以及种群进化的参考标准，这样不仅易造成种群进化方向短时间内偏离理论目标值的缺陷，而且会造成在有限的搜索时间内可能错失最优解。基于以上分析并结合前述研究成果，本文提出了基于3层融合思想的小生境遗传退火算 法 （niche genetic simulated annealing algorithm，NGSA），采用小生境思想来实现遗传算法的选择操作，通过相似个体种群中选择概率的不均衡分配，从而有效避免算法落入局部陷阱，改善了搜索初期有效基因的缺失问题；采用GA和SA相结合的串行搜索结构来提高参数对算法性能作用的鲁棒性，充分利用GA的全局和SA的局部搜索能力，把SA的处理结果转变为GA进一步优化的初始种群，使算法的全局寻优能力得到明显提高；采用精英保留策略的进化信息共享机制，在进化的每个阶段保留最优解个体，指导算法的进化方向；采用自适应交叉和变异概率相结合的方法来提高算法进化的速度，并将之与其他算法进行对比，以考察其有效性，然后把该算法用于车间调度，以验证其在解决该类调度问题时的优良性能。

1 NGSA算法

小生境遗传退火算法的执行过程由三部分组成：首先通过小生境的浓度控制机制实现优秀个体的选择，然后通过自适应遗传算法的进化操作（侧重全局搜索）产生较优良的一个群体，再利用模拟退火操作（侧重局部搜索）来进行基因个体的优化调整，运行过程反复迭代，直到满足终止条件为止。这种算法思路着眼于从全局最优解的搜索角度和算法的进化速度上来提高算法的性能，其流程如图1所示。

小生境遗传退火算法的生成步骤可描述为：

（1）设置进化代数计数器t＝1，随机产生含m个个体的初始种群pop0（t），同时计算各个个体的适应度fi，i＝1，2，…，m。

（2）对种群pop0（t）中的个体按其适应度大小降序排列，并把适应度最高的个体和目标值保存在最优解集中。

（3）判断是否满足收敛条件，若满足终止条件，则终止运算，输出计算结果；如不满足终止条件，转（4）。

（4）小生境浓度控制运算选择程序为：将第（1）步得到的m个个体，按照下式求出每2个个体a和b适应度之间的海明距离：

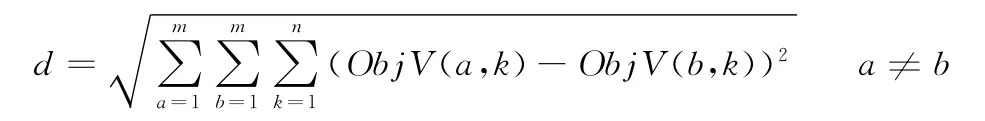
式中，ObjV为个体目标值；k为求解问题的决策变量个数。

当d＜L（L是预先指定的小生境之间的距离参数）时，比较个体和个体的适应度大小，并对其中适应度较低的个体处以罚函数fmin（xi，xj）＝Fpenalty，以极大地降低其适应度，即增加其被淘汰的概率。

（5）采用遗传算法进行选择、交叉和变异等操作，以生成群体pop2（t）。其过程为：①对种群pop0（t）进行预选择操作，选择操作时，先进行赌盘选择，再采用精英选择，其每个个体的被选择概率为

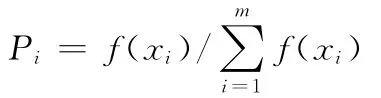
在选择的过程中使用保优原则，即上一代最优的个体以概率1保存至下一代；②采用自适应交叉算子对种群pop0（t）进行交叉操作，从而得到种群pop1（t）；将最优解存入知识库，在搜索过程中首先查询知识库，以避免最优解的丢失，提高种群的进化能力；③采用自适应均匀变异算子对种群pop1（t）进行变异操作，从而获得种群pop2（t）。

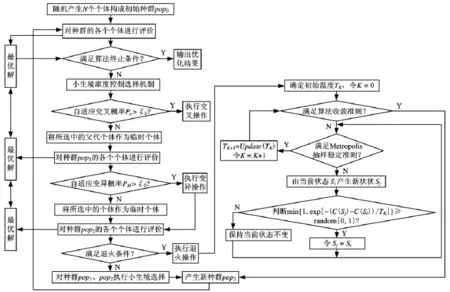
图1 小生境遗传退火算法流程图

（6）用“黄金分割”率进行退火操作选择，如果满足退火条件（I＝1），则执行步骤（7），否则（I＝0）执行步骤（8）。其执行过程为：①定义“黄金分割”点G1、G2和退火温度控制值DD，G1＝G2－round（0.618 G2），G2＝ maxGen － round（0.618 maxGen），其中 maxGen 为最大循环代数；②根据循环代数j判断是否执行退火操作，具体伪代码如下：

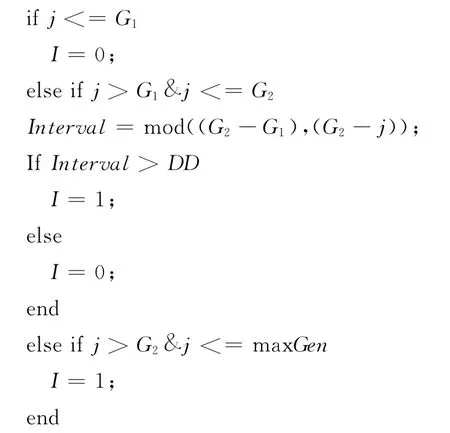
（7）以pop2（t）为初始种群，对其中各个个体进行模拟退火运算，即在绝对温度T，由当前状态i产生新状态j，两者的能量分别为Ei和Ej。若Ej＜Ei，则接受新状态j为当前状态；否则，若概率Pr＝exp［－（Ej－Ei）／（k0T）］大于［0，1］区间内的随机数，则仍旧接受新状态j为当前状态，若不成立则保留状态i为当前状态，其中k0为Boltzmann常数。对得到的规模为m的新群体pop3（t）的个体按其适应度大小降序排列。

（8）将pop1（t）、pop2（t）合并构成一个新群体，并对其进行适应度排序，更新pop3（t）中个体，并转步骤（2）。

从小生境遗传退火算法的优化流程，可归纳出该算法的如下特点：

（1）算法机制的融合。小生境遗传退火算法实现了基于优胜劣汰思想的群体遗传操作优化和基于退温历程控制实现最优解搜索方法的融合。

（2）算法结构的互补。小生境浓度控制机制优化初始种群的选择机制是，把经过GA进化的结果作为SA串行优化的初始解，经Metropolis抽样过程得到的解又成为GA进一步进化的初始种群。

（3）算法操作的结合。小生境操作使个体在整个约束空间中分散开来，增强了种群的多样性。GA的选择操作有利于优化过程中产生优良模态的冗余信息；交叉操作有利于后代继承父代的优良模式；精英保留策略，可充分利用历史信息指导搜索行为。

2 算法性能分析

为了验证上述小生境遗传退火算法的求解效率、有效性和可靠性，采用3个典型的非线性函数进行对比验证，其各自的表达式分别为

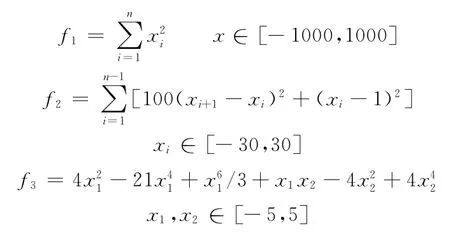
［6-7］分别采用f2和f3验证其算法性能的方法，将函数f1、f2、f3各自独立运行20次后的结果与其他算法结果进行对比，对比结果如表1所示。各种实验方法的参数如下：①遗传算法的交叉和变异概率分别为0.85和0.1；②小生境遗传退火算法寻优参数精度为1×10－4，自适应交叉概率为［0.6，0.99］，自适应变异概率为［0.01，0.1］，距门限上界距离为3，初始温度为100K，温度降低参数为0.98，退火温度控制值为0.15；③退火遗传算法种群规模为100，进化代数为800，交叉和变异概率分别为0.7和0.1，初始温度为100K，温度降低参数为0.98；④改进协同粒子群分为5个子群，种群规模为100，进化代数为800，惯性权重为0.4，学习因子c1＝c2为1.49，扰动因子为150；⑤混合量子遗传算法变量精度为10－5，交叉和变异概率分别为1和0.05。图2所示为遗传退火算法f2函数优化结果。图3所示为小生境遗传退火算法f2函数优化结果。

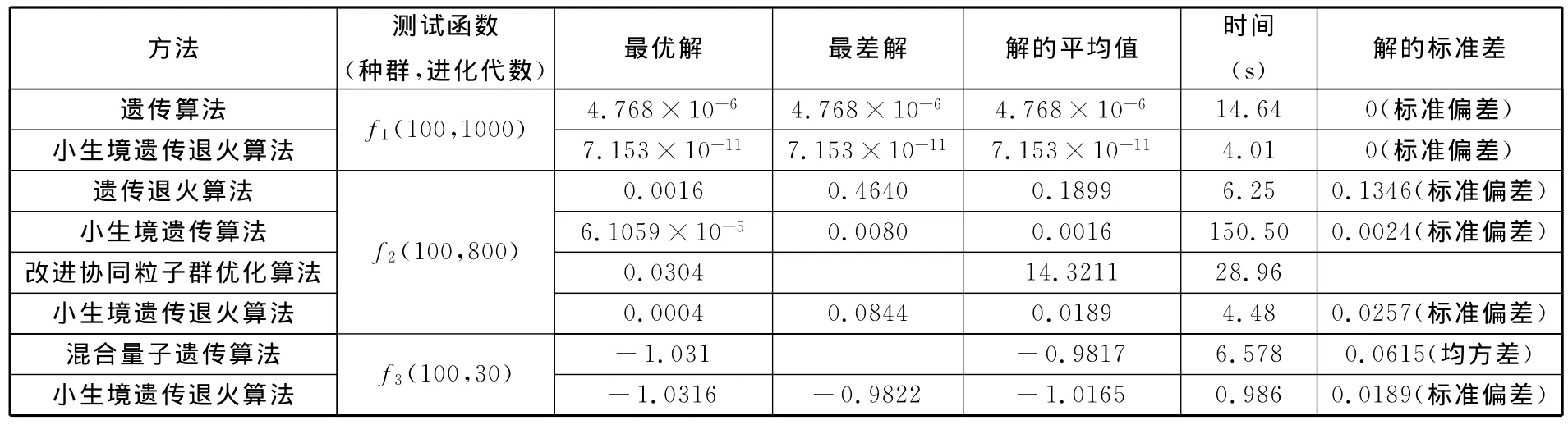
表1 各种方法的性能比较

图2 终止代数为800的适应度曲线遗传退火算法f2函数优化

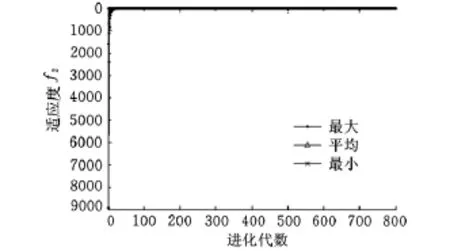
图3 小生境遗传退火算法f2函数优化

由表1和图2、图3分析可知：

（1）在优化函数f1时，相同的种群规模及进化代数下，小生境遗传算法比遗传算法收敛速度更快，达到更优的解，同时搜索过程表现出稳健性。

（2）在优化函数f2时，小生境遗传退火算法收敛速度最快，能搜索到较优解，小生境遗传算法所求解的平均值和偏差最小。另外，小生境遗传退火算法的寻优时间比小生境遗传算法约快34倍，节省了大量的资源消耗，且求解过程稳定，平均值波动小。

（3）在优化函数f3时，与混合量子遗传算法相比，小生境遗传退火算法表现出更快的收敛速度，更强的搜索能力。

数值实验证明，NGSA混合算法在搜索能力和优化效率等方面具有明显的优越性。

3 算法在车间调度中的应用

3.1 车间调度问题描述

n个工件J1，J2，…，Jn在m 台机器M1，M2，…，Mm上加工，工件之间的加工顺序无约束，每个工件的Ni（i＝1，2，…，n）个工序有先后约束，Ji＝Ji1，Ji2，…，Jil为工件Ji的工序序列，每道工序在固定的机器上加工。调度的目标是最小化最大完工时间，其数学描述为

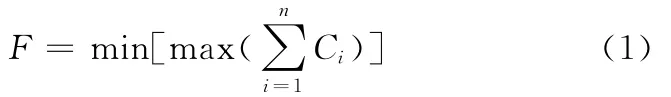
约束条件：

（1）工序约束。前道工序完成以后才能开始后道工序的加工。其数学表述为

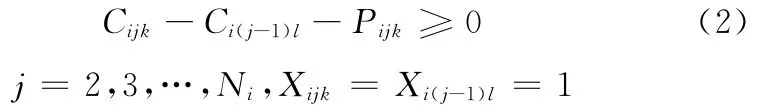
（2）机器约束。同一台机器k上，一个加工任务完成后才能开始另一个加工任务。其数学表述为

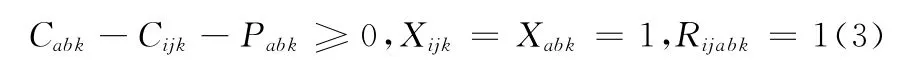
（3）完成时间约束。其数学表述为

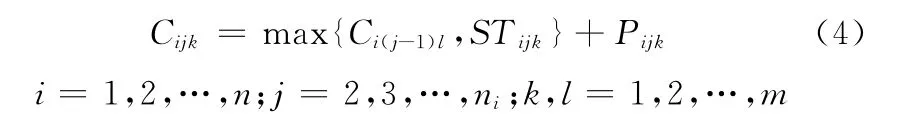
式中，Ci（j－1）l为工件Ji的完工时间；Pijk为工件i的第j道工序在机器k上的加工时间；Cijk为工件i的第j道工序在机器k上的完成时间；STijk为工件i的第j道工序在机器k上的开始加工时间。

工件i的第一道工序的完成时间Ci1k须满足约束：

（4）每个工件的每道工序在任何一台机器上加工时不允许中断。

（5）所有工件在零时刻都可以被加工。

3.2 算法实现

3.2.1 算法编码

在初始化过程中，本文采用基于工序的表达法进行编码，如针对表2中的3×3问题，假设给定的染色体为［321123123］，其中1代表工件J1，2代表工件J2，3代表工件J3，因为每个工件有3道工序，所以每个工件在一个染色体中刚好出现3次，染色体与工件的对应关系如图4所示。

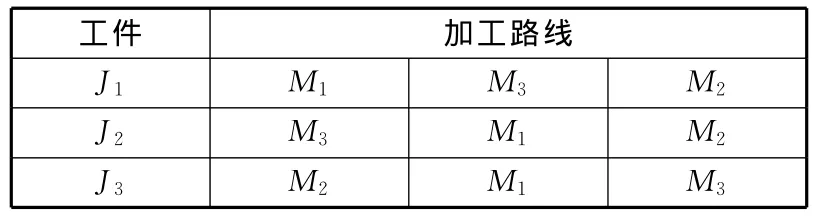
表2 3个工件、3台机器的车间调度问题

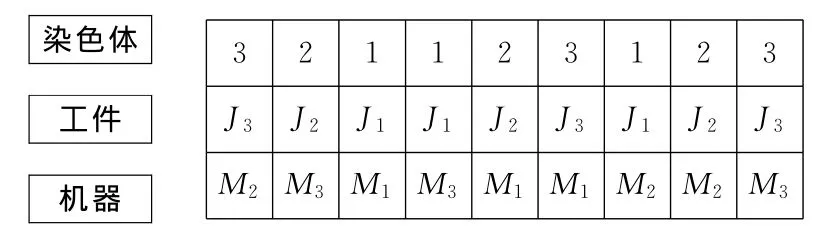
图4 染色体、工件和机器的对应关系

3.2.2 基于共享机制的小生境技术

基于共享机制的小生境实现方法是由Goldberg于1987年提出的。主要通过共享函数调整个体适应度来维持种群的多样性。其过程为：先根据个体之间的海明距离定义个体的共享函数，然后通过共享函数调整种群中每个个体的适应度，并把调整后的适应度作为遗传算子的依据。这种小生境技术限制了群体内某一特殊物种的无限制增长，对保证解的多样性无疑是有效的，提高了获得最优解的概率［8］。涉及的主要定义如下：

定义1 所谓个体之间的距离是指2个个体基因或基因表现形式之间的差异，记为d（i，j）。本文采用海明距离公式来描述种群中个体ci与cj之间的差异。其数学表述为

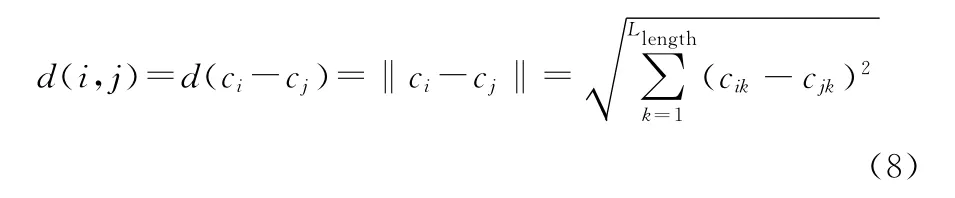
式中，Llength为个体染色体长度。

式（8）中的d越大，则表示车间调度问题的排序差异越大。

定义2 共享函数用来衡量2个个体之间的密切程度，本文采用三角函数作为共享函数。其数学表述为

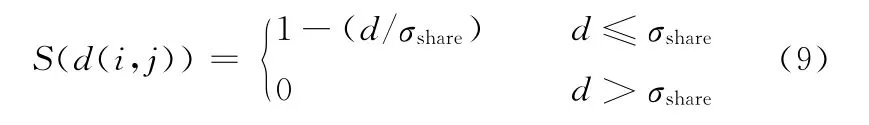
式中，σshare为小生境半径。

定义3 个体的共享度即指个体的小生境数，定义种群中个体的小生境数为该个体与种群中其他个体的共享函数值的和［9］。个体在种群中的共享程度用共享度进行衡量，记为Si，从而每一个体在种群中的共享度可描述为

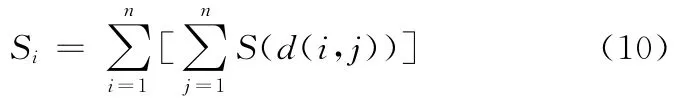
式中，n为种群规模。

式（10）中的Si越大，则表示围绕该个体的其他个体数量越多。当个体的共享度值确定以后，种群个体的适应度函数即调整为

式中，fi为个体i调整前的适应度；f′i为个体i调整后的适应度。

式（11）中的共享度Si越大，经调整后的适应度f′i就越小，从而达到抑制适应度高的个体无限制增长的目的［10－11］。共享机制小生境伪代码如下：

3.2.3 自适应双点交叉操作

交叉操作是遗传算法中增加种群多样性，防止算法早熟、停滞的操作。为充分利用历史信息，本文采用双点交叉，如图5所示。

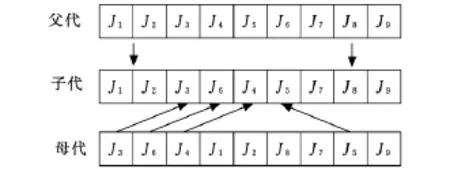
图5 双点交叉

在进化的过程中，为达到较快的搜索速度，当前代种群中个体的适应度低于平均适应度值时，就需要提高交叉率；当适应度值高于平均适应度值时，则需要降低交叉率，这样就需要交叉率随着适应度值自动地调整。为此，本文提出交叉概率动态调整策略，交叉率的自适应调整公式为

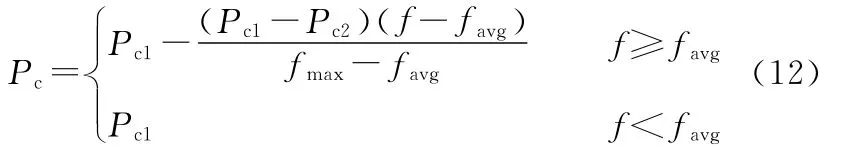
式中，Pc1、Pc2为交叉概率，且Pc1＞Pc2。

3.2.4 自适应随机变异操作

变异是按一定的概率改变个体基因链，变异操作的目的是维持群体的多样性，改善局部的搜索能力，同时防止出现早熟现象。为增加种群多样性，本文采用随机互换变异，如图6所示。

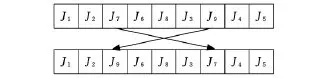
图6 随机互换变异

随机选择染色体中的两基因位，交换其值。同样采用自适应变异概率来提高收敛速度，自适应调整公式为

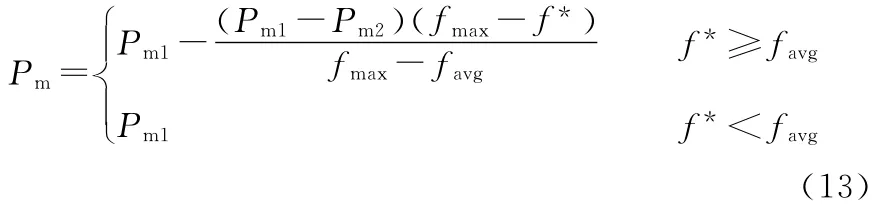
式中，Pm1、Pm2为变异概率，且Pm1＞Pm2。

3.2.5 精英保留策略

在传统遗传算法中，由于遗传算子操作具有随机性，可能造成最优个体的丢失，进而导致收敛周期较长。同样，小生境共享机制的引入，虽然增大了个体的搜索空间和收敛到最优解的概率，但却导致进化过程漫长，收敛进度缓慢。为解决上述2个问题，本文引入精英保留策略，其伪代码如下：

3.3 仿真实验

在Pentium 4计算机上（CPU主频为2.71GHz、内存为1.75GB、操作系统为 Windows XP），利用MATLAB 2009仿真工具编程实现上述算法。设置的算法基本运行参数为：群体规模500，最大迭代数100，交叉率0.6，变异率0.06，衰减参数0.95，迭代初始温度500K。经过20次测试，得到表3所示的结果。

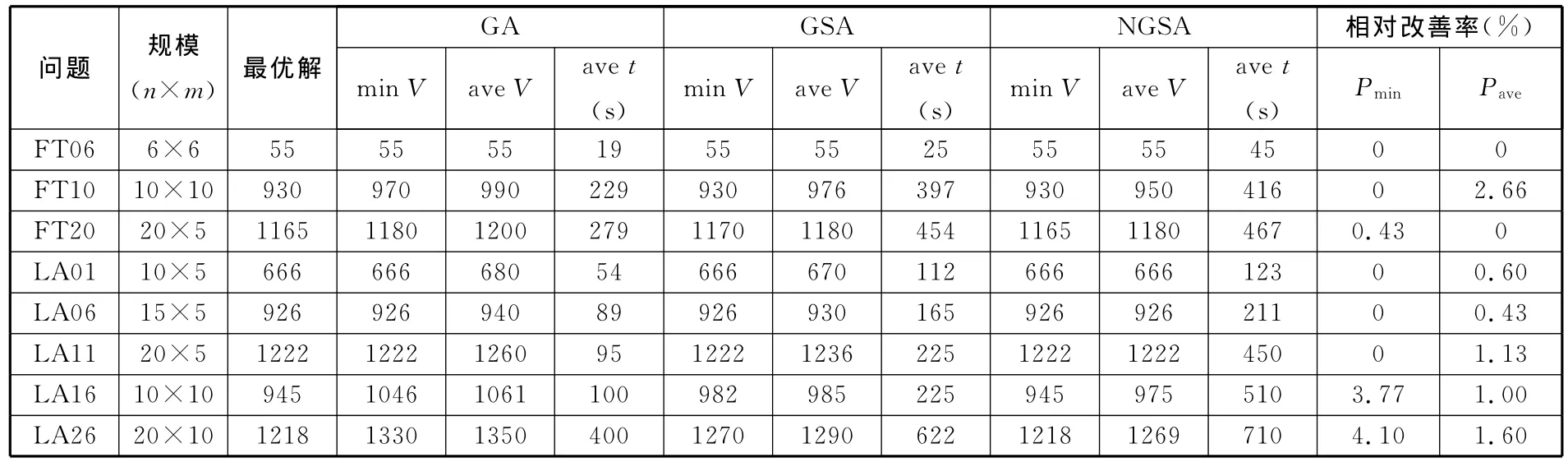
表3 20次实验各种算法最优结果比较

表3中的min V、ave V和ave t分别为最小值、平均值和平均时间；Pmin、Pave分别为最小值相对改善率、平均值相对改善率。其计算公式为

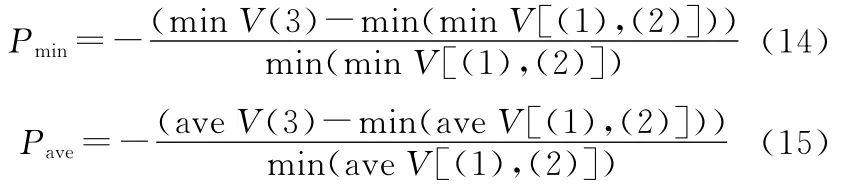
从表2可以得出：

（1）在FT类问题求解方面，3种算法都能绝对收敛到FT06的最小值，其中，本文所提小生境遗传退火算法平均收敛时间最长，可见，在小规模问题上，该方法没有表现出本身的优势；对于FT10标准问题，小生境遗传退火算法和遗传退火算法都可以收敛到最小值，小生境遗传退火算法平均值的相对改善率为2.66%；对于FT20标准问题，只有小生境遗传退火算法可以收敛到最小值，并且最小值相对改善率为0.43%。

（2）在LA 类问题求解方面，对于LA01、LA06、LA11标准问题，3种算法都可以收敛到最小值，同时，小生境遗传退火算法与其他2种算法相比，其平均值相对改善率分别为0.60%、0.43%和1.13%；对于LA16、LA26标准问题，在可接受的收敛时间范围内，小生境遗传退火算法与其他2种算法相比，其最小值和平均值都有所改善。

4 结论

（1）本文提出的小生境遗传退火算法，通过相似个体群中选择概率的不均衡分配增加了种群的多样性，有效避免了算法掉入局部陷阱，提高了算法的全局收敛性能；通过自适应交叉和变异操作提高了算法的进化速度；通过精英保留策略，利用优良的染色体模板，使个体在迭代过程中有效地继承了父代的优良特征，避免了最优解的丢失，确保了搜索过程加速向最优的方向逼近。

（2）本文提出的小生境遗传退火算法，注重算法机制的融合，实现了基于优胜劣汰思想的群体遗传操作优化（侧重全局搜索），以及基于退温历程控制来实现最优解搜索方法（侧重局部搜索）的融合。注重算法搜索结构的互补，实现了遗传算法的并行搜索与模拟退火算法的串行搜索的互补。重视算法操作的融汇和结合，实现了小生境操作增强种群多样性的目的，亦即：选择操作能从多样性群体中选择优良个体；交叉操作能让后代继承父代的优良模式；变异操作能以优良个体为模板拓宽最优解的搜索范围；精英保留操作能充分利用小生境操作、交叉操作和变异操作等进化过程历史信息指导搜索行为。

参考文献：

［1］梁旭，黄明，常征.求解车间调度问题的一种新遗传退火混合策略［J］.计算机集成制造系统，2005，11（6）：851－854.

［2］张昊，陶然，李志勇，等.基于自适应模拟退火遗传算法的特征选择方法［J］.兵工学报，2009，30（1）：81－85.

［3］潘全科，王文宏，朱剑英.一类解决车间调度问题的遗传退火算法［J］.机械科学与技术，2006，25（3）：317－321.

［4］刘敏，严隽薇.基于自适应退火遗传算法的车间日作业计划调度方法［J］.计算机学报，2007，30（7）：1164－1172.

［5］冯毅，李利，高艳明，等.一种基于小生境的混合遗传退火算法［J］.机械科学与技术，2004，23（12）：1494－1498.

［6］虞斌能，焦斌，顾幸生.改进协同粒子群优化算法及其在Flow Shop调度中的应用［J］.华东理工大学学报（自然科学版），2009，35（3）：468－474.

［7］王凌，吴昊，唐芳，等.混合量子遗传算法及其性能分析［J］.控制与决策，2005，20（2）：156－158.

［8］Jia Chunqiang，Yu Ling，Shu Jun，et al.Optimal Design of Hydraulic Manifold Blocks Based on Niching Genetic Simulated Annealing Algorithm［J］.High Technology Letters，2007，13（4）：363－368.

［9］Sadegheig A.Scheduling Problem Using Genetic Algorithm，Simulated Annealing and the Effects of Parameter Values on GA Performance［J］.Applied Mathematical Modelling，2006，30（2）：147－154.

［10］Andresen M，Brasel H，Morig，et al.Simulated Annealing and Genetic Algorithms for Minimizing Mean Flow Time in an Open Shop［J］.Mathematical and Computer Modelling，2008，48（7／8）：1279－1293.

［11］Pere E，Herrera F，Hernandez C.Finding Multiple Solutions in Job Shop Scheduling by Niching Genetic Algorithms［J］.Journal of Intelligent Manufacturing，2003，14：323－339.