轴承滚子电化学机械光整加工表面质量预测与加工参数选择

徐文骥 魏泽飞 孙 晶 李 强 余自远 庞桂兵

1.大连理工大学，大连，116024 2.大连工业大学，大连，116034

0 引言

滚动轴承广泛应用于机床、汽车、电机及其他设备中，其主要失效形式为磨粒磨损与疲劳磨损［1－4］。随着现代机械在高速、重载、低噪声及低振动等方面的要求的提高，不但对滚子表面加工质量要求越来越高，而且还对滚子表面有凸度要求，以减小应力集中。由于加工中存在热变形、加工误差、残余应力以及机床振动等影响，实际加工出的滚子常与理论设计存在偏差，导致轴承运转提前失效。理论与实践表明，较低的滚子表面粗糙度值，不但可降低机器的振动与噪声，还可大幅提高其使用寿命［5－6］。

目前，轴承滚子精加工方法主要是磨削后再超精加工，表面质量受磨轮与导轮影响较大，不易控制。电化学机械光整（electrochemical mechanical finishing，ECMF）加工将电化学阳极溶解与机械磨削加工相结合，对金属零件表面进行光整加工。由于ECMF具有不受材料硬度限制、凡导电材料均可加工，以及无加工热影响区等优点，在光整加工领域备受关注［7－8］。ECMF加工的“尖端效应”，不但可使零件表面的波峰凸起优先溶解去除，而且可修正零件的圆度。但ECMF加工系统是一个复杂的非线性系统，加工过程中的参数，包括加工间隙、电流密度、电解液浓度、机械压力，以及磨粒粒度等都会对工件表面质量产生影响，难以建立其精确的ECMF加工表面质量预测模型。

近来，支持向量机（support vector machines，SVM）作为一种流行的机器学习算法，由于其显著的泛化能力，引起了广泛关注并获得大量应用。由Suykens等［9］提出的最小二乘支持向量机（least squares support vector machines，LSSVM）作为SVM的一种新扩展，降低了计算复杂性，具有更快的速度以及更好的鲁棒性，被成功地应用于汽车、电力电子、计算机，以及生物医学等领域的控制预测模型中，并获得了较好的效果［10－16］。

本文首先建立轴承滚子的ECMF加工装置，并对轴承滚子进行光整加工。其次，将LSSVM引入轴承滚子的ECMF加工中，建立了基于LS－SVM的轴承滚子ECMF加工质量及参数预测模型，并通过正交试验确定训练样本。最后，为提高预测模型的精度，使用网格搜索法确定LS－SVM的预测参数，对表面质量和加工参数进行预测和选择，获得了比较好的效果。

1 LS－SVM 原理

设训练样本集D＝｛（｜xk｜，｜yk｜）｜k＝1，2，…，N｝，其中xk∈RN是N维输入数据，yk∈RN是N维输出数据。非线性回归就是找到一个非线性映射函数φ（x），能够逼近输入和输出之间的关系：

式中，w为权向量；φ（x）为映射函数；b为偏差量。

将原始输入数据映射到高维空间，在此空间中构建线性回归方程，将原空间中的非线性不可分问题转化成线性可分问题。优化问题的回归模型为

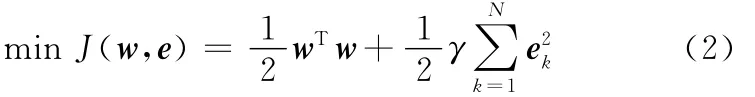
其约束条件为

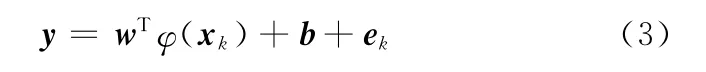
式中，γ为可调常数；ek为误差变量。

为找到最优参数使得回归模型式（1）中的预测误差达到最小，引入Lagrange函数：

式中，α为拉格朗日乘子。

对w、b、e和α求偏微分可得

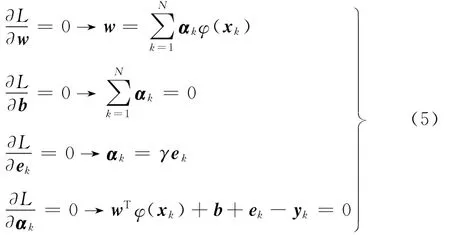
式（5）消去w和γ可得

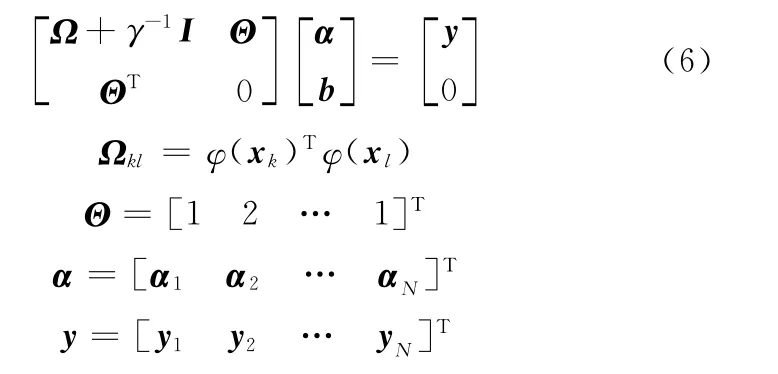
式中，Ω为正方形矩阵；I为单位矩阵。

通过求解式（6），可得参数α和b的值。

LS－SVM的函数估计为［15］

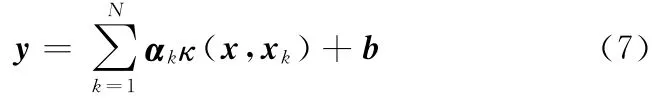
式中，κ（x，xk）为核函数。

LS－SVM常用的核函数主要有：多项式核函数（polynomial kernel）、Sigmoid核函数、线性核函数（linear kernel）和径向基函数（RBF）。相对于其他3种核函数，径向基函数可以将训练样本映射到更高维的特征空间，有助于解决系统指标参数与工艺参数间的高度非线性关系。此外，以径向基函数为核函数的SVM模型更简单、所需输入参数少，可减少因选取样本参数的不当所造成的预测结果偏差［14］。本文选择满足 Mercer条件的对称函数κ（x，xk），径向基核函数（radial basis function，RBF）可表示为

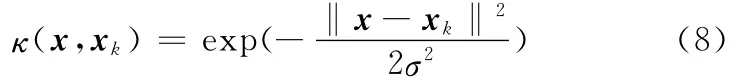
式中，σ为核宽度。

将式（5）、式（8）代入式（7）中，即可得到采用RBF的LS－SVM模型表达式：

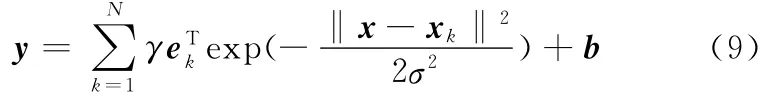
通过调节式（9）中的参数γ和σ，能获得较高的预测精度。

2 轴承滚子ECMF加工

2.1 ECMF加工装置

图1所示为滚子的ECMF加工装置示意图。工件阳极3与电源1的正极相连，并在驱动轮9的带动下以一定速度旋转，工具阴极2与电源负极相连，并与工件保持一定间隙，中间高速流过经泵7泵出的电解液，带走反应产物及热量。油石4在气缸5的推力作用下与工件保持一定压力。

2.2 实验材料与方法

试件采用NJ212M型轴承滚子，尺寸为φ12mm×12mm圆柱体，材料为GCr15，其化学成分如表1所示。试件经丙酮溶液清洗除油，去离子水、无水乙醇溶液清洗后烘干。阴极材料选用紫铜，面积为1.2cm×0.4cm。电解液采用质量分数为18%的中性NaNO3水溶液，流速为25L／min，主要加工参数如表2所示。工件表面粗糙度及凸度采用Talysurf SLI2000型三维形貌轮廓仪测量，圆度采用Talyrond 365－500型圆柱度测量仪测量。

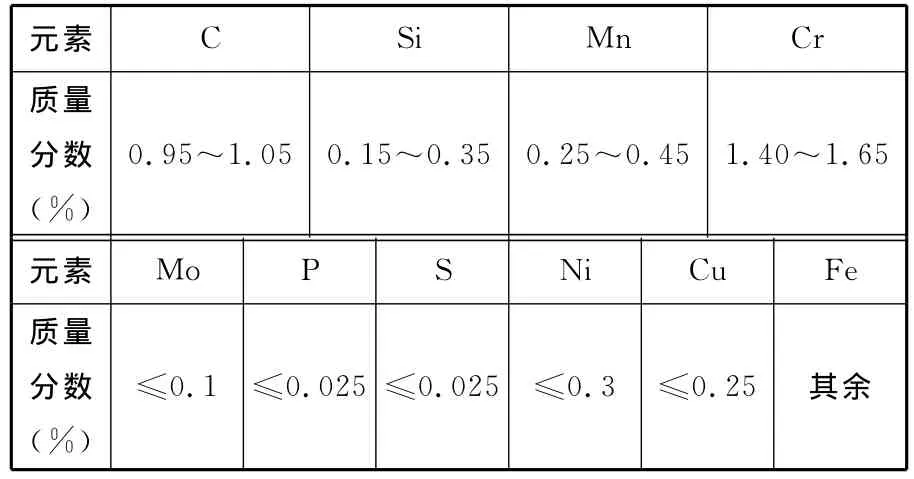
表1 GCr15化学成分

表2 ECMF加工实验参数

2.3 实验设计

根据ECMF加工原理，影响表面质量的因素有工件转速、极间间隙、油石压力、电流密度、油石粒度、加工时间、电解液浓度及流速等。加工过程中表面质量能否达到要求取决于以上各参数的合理匹配，若各参数匹配得当，则可得到较低的表面粗糙度值；若匹配不当，则零件表面易出现斑点腐蚀、晶界腐蚀和表面划伤等缺陷。本文正交试验设计为L16（45），选取的5个参数为：工件转速n、油石压力p、电流密度i、油石粒度ξ、加工时间t，作为影响表面质量Ra的主要因素，其四水平值如表2所示。1～16组实验数据将作为LS－SVM的数据样本，对预测模型进行训练；另外再做4组实验（表中带＊号的数据），即17＊～20＊组数据用于对模型的精度进行验证。因此，输入及输出数据集分别为：x＝｛n，p，i，ξ，t｝，y＝｛Ra｝。20组实验数据如表3。

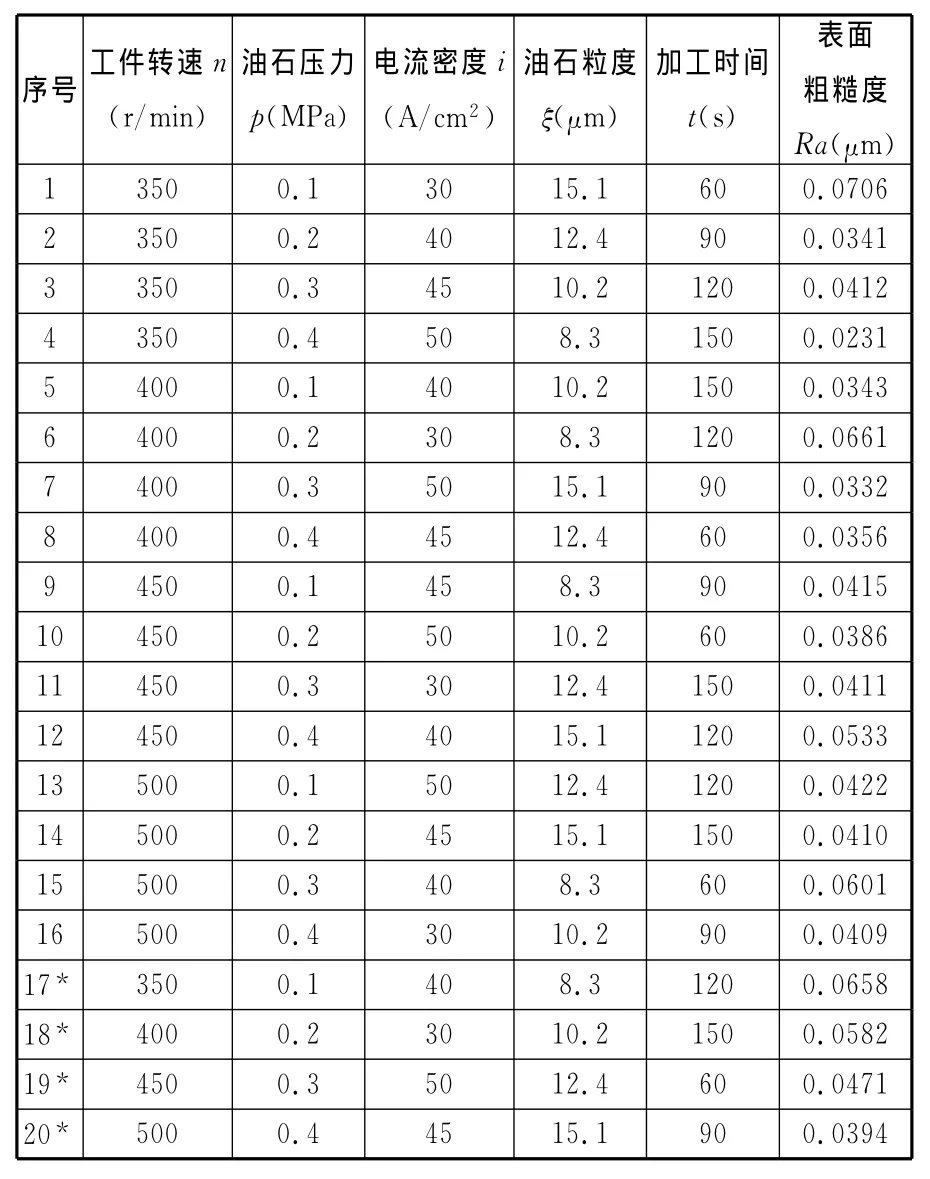
表3 ECMF加工实验数据

2.4 实验结果

图2所示为ECMF加工前后滚子表面，由图2可知，加工后表面质量明显提高，达到镜面效果。图3所示为ECMF加工前后滚子表面粗糙度，由图3可知，表面粗糙度Ra从加工前0.0874μm降低到加工后的0.0231μm；轮廓最大高度Rz由0.772μm 降低到0.292μm（第4组）。图4所示为ECMF加工前后滚子圆度变化，圆度Ro由加工前的0.93μm降低到加工后的0.39μm（第4组）。

3 ECMF加工质量预测及加工参数选择

3.1 数据预处理方法

为防止某个参数的异常对训练模型精度产生影响，数据在训练前要进行归一化处理，使输入输出数据归一化在［0，1］区间内［17］。归一化公式为

式中，unor为归一化后数据；u为原始输入及输出数据；umin、umax为原始输入及输出数据的最小值与最大值。

经LS－SVM预测后的数据，再经下式反求原始数据：

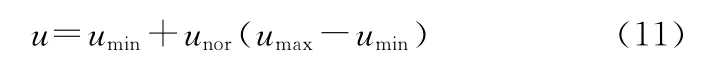
3.2 误差分析方法

参见式（9），为提高预测模型精度，加快模型收敛速度，须调节参数γ和σ。目前还没有规范统一的γ和σ选取方法，一般采用网格搜索法或试选法［15］。本文采用网格搜索法，即给定γ和σ的选取范围，组成交叉网格，对每一组γ和σ数据进行训练，选取预测误差最小者作为最终取值。考虑到式（9）中的σ以σ2形式存在，所以，为方便计算，下文中使用σ2计算。

为评价参数γ和σ2对应的模型预测精度，引进误差函数：平均绝对百分误差eM和均方根相对误差eR，其表达式分别为

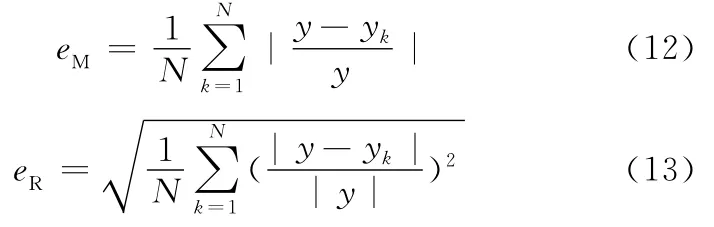
式中，yk为模型的输出值；y为实测值；N为样本数量。

3.3 表面质量预测

利用表3的实验数据构造LS－SVM回归模型的训练样本集｛xk，yk｝，其中输入参数xk为多维向量，包括工件转速（n）、油石压力（p）、电流密度（i）、油石粒度（ξ）、加工时间（t），是影响工件表面粗糙度的主要加工参数。输出参数yk为k号工件的表面粗糙度。

利用LS－SVM回归算法对训练样本集进行辨识，本文以表3中的1～16组数据作为训练样本，建立并训练预测模型。LS－SVM算法直接利用MATLAB软件工具箱进行计算，选用式（9）的RBF径向基函数作为核函数，其中γ的范围试选为｛0.5，1，…，500｝，σ2取值范围为｛0.05，0.1，…，500｝，构建搜索网格，经式（12）、式（13）计算，选取常数γ＝16.5，σ2＝8.1时训练结果误差最小，模型训练结果如图5所示。

用表3中的17＊～20＊组实验数据验证所建立的预测模型精度，将加工工艺参数xk输入到LS－SVM预测模型，得到响应yk，即为该工件表面粗糙度的预测值。与工件的实际表面粗糙度的测量值进行对比，可得到表面质量的预测误差。预测值与实际值的对比如图6所示。经式（12）、式（13）计算可知，误差eM为5.4%，eR为6.5%。

3.4 加工电流密度选择

实际的加工过程受到加工质量和成本要求等约束，通常采用试加工或反复实验法来选择合适的加工参数。但前者难以达到较高的加工效率，也不易获得要求的加工质量；后者效率低、加工成本高。若能选定优化的加工参数，就可以直接获得所需要的表面质量，不但能提高加工效率，而且还可以降低加工成本。

表4所示为正交试验因素分析，由表4可知，极差R反映各因素对结果的影响重要程度，表中的各实验参数对表面质量的影响顺序由高到低依次应为：电流密度i（R＝0.0809）、加工时间t（R＝0.0654）、油石粒 度ξ（R ＝0.0451）、油 石压力p（R＝0.0357）、工件转速n（R＝0.0152）。其中电流密度i对表面质量的影响最大，因此，预先确定电流密度值比其他参数的选择相对重要。这里仍采用LS－SVM对加工参数进行选择。此时，将电流密度设为输出值，而其他参数设为输入向量，重新建立预测模型，如图7所示，图中，调节参数γ＝52，σ2＝61。图8所示为电流密度预测数据与实验数据的对比，其中，误差eM＝4.8%，eR＝6.6%。

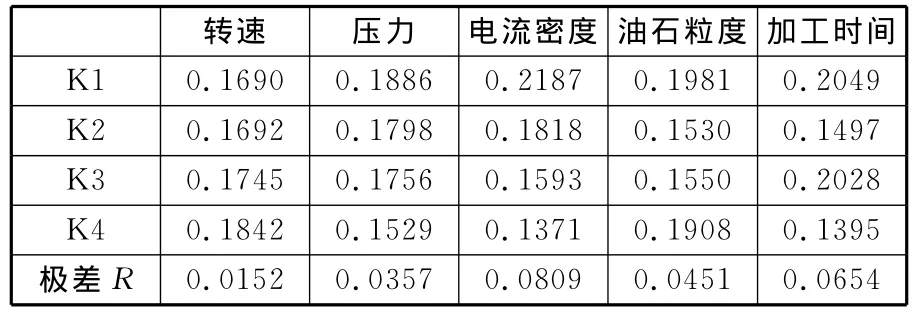
表4 正交试验因素分析

3.5 其他加工参数的选择

实际上，其他加工参数也可以采用3.4节方法进行优化确定。图9所示为加工时间预测值与实验值的对比结果，其中，γ＝104，σ2＝80，eM＝5.5%，eR＝7.6%。图10所示为磨料粒度预测值与实验值的对比结果，其中，γ＝65，σ2＝88，eM＝1.9%，eR＝2.2%。图11所示为油石压力预测值与实验值的对比结果，其中，γ＝92，σ2＝130，eM＝4.5%，eR＝6.2%。图12所示为工件转速预测值与实验值的对比结果，其中，γ＝50，σ2＝320，eM＝2.7%，eR＝3.7%。

4 结论

（1）本文建立了轴承滚子的ECMF加工装置，采用ECMF方法加工轴承滚子。通过实验结果可知，采用ECMF加工轴承滚子是可行的。加工后的滚子表面粗糙度达到0.023μm，圆度达到0.39μm，有效改善了滚子表面质量。

（2）将LS－SVM引入轴承滚子ECMF加工中，建立了基于LS－SVM的轴承滚子ECMF加工预测模型，对轴承滚子的表面质量进行预测的。结果表明，所建立的LS－SVM模型预测效果比较符合实际加工效果，预测误差eM为5.4%，eR为6.5%。

（3）通过正交试验法，得出影响ECMF加工的主要因素为电流密度。利用LS－SVM预测模型，对ECMF加工电流密度进行选择，其选择的eM为4.8%，eR为6.6%；选择的其他加工参数为：最大eM＝5.5%，最大eR＝7.6%。

［1］Neagu－Ventzel S，Cioc S，Marinescu I.A Wear Model and Simulation of Superfinishing Process：Analysis for the Superfinishing of Bearing Rings［J］.Wear，2006，260（9／10）：1061－1069.

［2］于志强，杨振国.SKF滚动轴承的失效分析［J］.金属热处理，2007，32（增刊）：359－364.

［3］Galda L，Koszela W，Pawlus P.Surface Geometry of Slide Bearings After Percussive Burnishing［J］.Tribology International，2007，40：1516－1525.

［4］李鹏，闫振祥，解传宏，等.抽油机减速器滚动轴承失效形式及分析［J］.石油钻采工艺，2008，30（3）：142－144.

［5］Olofsson U.An Experimental Investigation of Wear and Fatigue Life Reduction of Boundary Lubricated Spherical Roller Thrust Bearings［J］.Tribology International，1997，30（9）：685－692.

［6］Iwamoto K，Tanaka K.Influence of Manufacturing Error of Roundness for Characteristics of Cylindrical Journal Bearing［C］／／Dowson D，Priest M，Dalmaz G，et al.Life Cycle Tribology Proceedings of the 31st Leeds－lyon Symposium on Tribology Held at Trinity and All Saints College.United Kingdom：Elsevier，2005：751－754.

［7］Seo Y.Electrochemical－mechanical Polishing Application：Monitoring of Electrochemical Copper Removal from Current－voltage Characteristics in HNO3Electrolyte［J］.Microelectronic Engineering，2011，88（1）：46－52.

［8］李邦忠，周锦进.不锈钢电化学机械镜面加工电解液研究［J］.中国机械工程，2004，15（11）：14－18.

［9］Suykens J A K，Gestel T V，Brabanter J D，et al.Least Squares Support Vector Machines［M］.New Jersey：World Scientific Publishing，2002.

［10］刘鸿博，罗陶涛.基于正交实验和最小二乘支持向量机的泡沫复合体系配方预测研究［J］.应用化工，2010，39（5）：713－715.

［11］Wong P K，Vong C M，Wong H C，et al.Modelling and Prediction of Spark－ignition Engine Power Performance Using Incremental Least Squares Support Vector Machines［C］／／Lu J W Z，Leung A Y T，Iu V P，et，al.Proceeding of the 2ND International Symposium on Computational Mechanics and the 12th International Conference on the Enhancement and Promotion of Computational Methods in Engineering and Science.Hong Kong– Macau：American Institute of Physics，2010：179－184.

［12］Vong C，Wong P，Li Y.Prediction of Automotive Engine Power and Torque Using Least Squares Support Vector Machines and Bayesian Inference［J］.Engineering Applications of Artificial Intelligence，2006，19（3）：277－287.

［13］林伟青，傅建中，许亚洲，等.基于最小二乘支持向量机的数控机床热误差预测［J］.浙江大学学报（工学版），2008，42（6）：905－908.

［14］曾杰，张华.基于最小二乘支持向量机的风速预测模型［J］.电网技术，2009，33（18）：144－147.

［15］Gencoglu M T，Uyar M.Prediction of Flashover Voltage of Insulators Using Least Squares Support Vector Machines［J］.Expert Systems with Applications，2009，36（7）：10789－10798.

［16］Guo Z，Bai G.Application of Least Squares Support Vector Machine for Regression to Reliability Analysis［J］.Chinese Journal of Aeronautics，2009，22（2）：160－166.

［17］Pyle D.Data Preparation for Data Mining［M］.London：Academic Press，1999.